

IGBT的关断瞬态分析—IV关系(1)
电子说
1.4w人已加入
描述
我们曾在文中反复提及,电压是电场的积分,而电场是电荷的积分,所以要得到电压的关断瞬态,就必须弄清楚电荷的分布以及积分的边界。
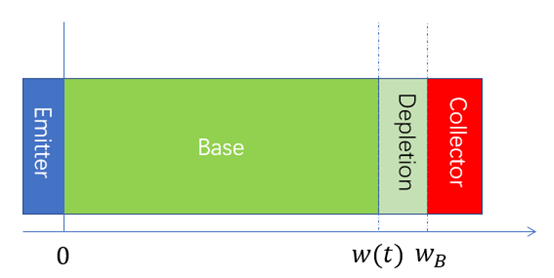
如图所示,关断过程中,电场只存在于耗尽区(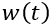 à
à 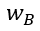 )中。耗尽区中的空间电荷浓度等同于基区的掺杂浓度,余下就需要弄清楚
)中。耗尽区中的空间电荷浓度等同于基区的掺杂浓度,余下就需要弄清楚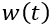 随时间的变化关系
随时间的变化关系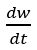 ,下面我们做一个简单的推导。
,下面我们做一个简单的推导。
根据泊松方程易知,耗尽区宽度的表达式为:
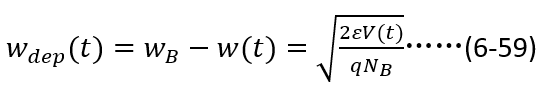
其中,  为外加电压(忽略了发射极的PN结电压),
为外加电压(忽略了发射极的PN结电压), 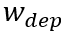 为耗尽区宽度。
为耗尽区宽度。
对(6-59)两边取平方,再对时间求导可以得到耗尽区宽度随时间变化率与电压随时间变化率之间的关系,如下,
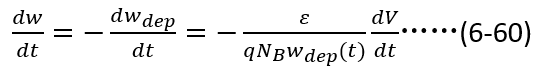
上式右边 实际上代表了单位面积的耗尽区电容,记为
实际上代表了单位面积的耗尽区电容,记为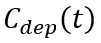 ,那么(6-60)可简化为,
,那么(6-60)可简化为,
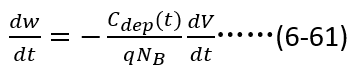
由此,我们建立了基区宽度与外加电压随时间的变化关系。回顾上一节,我们建立了基区宽度与多余载流子分布,进而与电荷总量以及电流之间的时间变化关系,那么以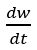 为纽带,就可以建立瞬态过程中的电流、电压之间的关系。
为纽带,就可以建立瞬态过程中的电流、电压之间的关系。
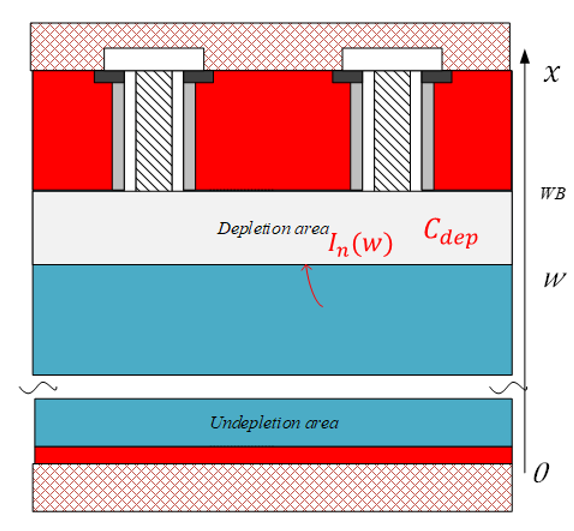
如图所示,可以将耗尽区扩展过程等效为结电容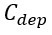 内部电场变化的过程,那么
内部电场变化的过程,那么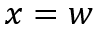 处的位移电流就代表了该位置的电子电流
处的位移电流就代表了该位置的电子电流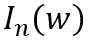 。
。
注:所谓位移电流,这里主要描述的是耗尽区内电场的变化,因此可以存在与真空或者介质中,并不会做功产生焦耳热;相对应的是传导电流,只能存在于导体中,定向移动则会做功产生焦耳热。因此电容变化过程中的关系可以书写如下:

(6-62)中除电流、电压外,还有一个电容随时间的变量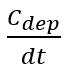 ,因为电容与基区宽度
,因为电容与基区宽度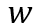 是相关联的,而后者又是与
是相关联的,而后者又是与 相关的,所以应该可以建立
相关的,所以应该可以建立 与
与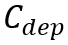 之间的关系,从而消除电容项。
之间的关系,从而消除电容项。
根据电容的定义表达式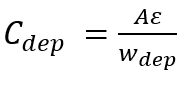 ,显然
,显然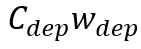 的乘积为常数,所以
的乘积为常数,所以
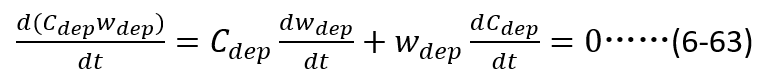
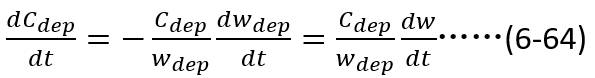
将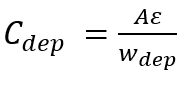 带入(6-64)再带入(6-62)结合式(6-59)即可消除电容项,得到电流与电压关系式。
带入(6-64)再带入(6-62)结合式(6-59)即可消除电容项,得到电流与电压关系式。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
IGBT关断过程分析2024-07-26 6816
-
IGBT的关断瞬态分析—电荷存储初始值2023-12-01 1294
-
igbt怎样导通和关断?igbt的导通和关断条件2023-10-19 26401
-
米勒电容对IGBT关断时间的影响2023-09-05 3345
-
IGBT关断时的电流和电压2023-02-22 848
-
讨论一下IGBT的关断过程2023-02-13 2123
-
IGBT的开启与关断2021-10-14 5483
-
IGBT栅极电压尖峰分析2021-04-26 8512
-
IGBT失效的原因与IGBT保护方法分析2020-09-29 5509
-
IGBT关断过程的分析2018-12-22 41270
-
高压IGBT关断状态失效的机理研究2016-05-16 970
全部0条评论

快来发表一下你的评论吧 !

