自动控制原理—分析闭环极点的方法

1

前言

对控制系统极点的分析唯一的目的，就是看看控制系统的动静态特性。先看稳不稳定，再看响应快不快。

学习了这么多年，自我感觉，对于搞工程实践而言，分析零极点能够达到定性分析系统响应的目的，但是定量就不可能了，毕竟采样环节的建模无论如何都不是很精确的。

而如果是搞理论的话，还是可以定量分析的，比如拿几个控制系统，把它们的极点画出来，就能直观的看出不同系统的优缺点了。

本文理论不深，就简要说说分析极点的方法吧。

2

二阶系统

由于大部分控制系统都是闭环的，因此本文所说的都是闭环系统的极点。接下来就把工程中常遇到的二阶系统进行讲解。

2.1 二阶系统什么样

就是这样：

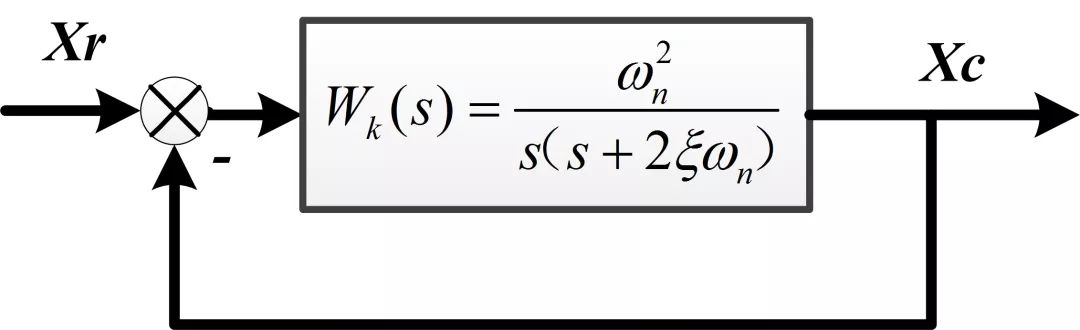
开环传递函数是：

闭环传递函数是：

其中，ξ为阻尼比，ωn为自然频率。

特征方程，就是求闭环传函分母等于零：

极点：

(1) 特征根的性质取决于ξ的大小；

(2) 二阶系统的响应时间取决于ξ和ωn两个参数。

2.2 过阻尼（ξ >1）

此时系统的极点都是实数。

(1) 对于过阻尼极点，它们的响应是按照指数形式，单调逐渐稳定到输入的。

(2) 极点距虚轴越近，对系统响应影响越大，且当ξ>>1时，影响度更大，此时可以忽略距离虚轴远的极点。

解释：二阶函数的时域阶跃响应如下：

设-p1<-p2<0，所以第一项衰减比第二项快，同第一项系数也比第二项小。进而可以得到，极点离虚轴越远，响应速度越快。

2.3 欠阻尼（0<ξ <1）

此时系统的极点都既有实部，又有虚部。

(1) 二阶系统的单位阶跃响应为衰减振荡曲线，且逐渐稳定到输入

(2) 系统的衰减程度与闭环的实部有关，离虚轴越远，衰减越快，这里与过阻尼特点一致。

(3) 系统的震荡程度与虚部有关，阻尼越小，超调越大。

解释：二阶函数的频域阶跃响应如下：

二阶函数的时域阶跃响应如下：

其中，θ为阻尼角，ωd为阻尼振荡频率。

整理：

极点的实部，出现在时域的指数上，为衰减项；

极点的虚部，出现在时域的正弦函数中，为震荡项；

2.4 稳定性

上面介绍的都是系统的暂态特性，下面说说系统的稳定性。

其实非常简单，我们只关注极点的实部。

从上面可知，无论是过阻尼还是欠阻尼，系统的指数项都是-pt。

1.当-p<0时，系统成指数衰减到稳态。
2.当-p>0时，系统随着时间在增加到无穷大，即系统发散，不稳定。

因此，闭环系统稳定的充要条件就是极点实部小于零，即系统所有闭环极点都在复平面的左半部分。

3

举一反三

上面介绍的性质亦可以引入到其它系统中，无论是多阶系统，过阻尼与欠阻尼。极点的性质都是一样的。

大家只需要记住：

(1) 闭环极点是成对出现的。

(2) 只要有极点在频率右半轴，系统就不稳定。

(3) 距离虚轴越远，对系统影响越小，甚至可以忽略。

(4) 极点的实部对应着系统的衰减项，距离虚轴越远，响应越快.

(5) 极点的虚部对应着系统的震荡项，阻尼越小，超调越大。

(6) 阻尼大于1，响应单调趋于稳定。阻尼小于1，响应震荡趋于稳定。

在分析高阶系统时，常常忽略距离虚轴较远的极点，使高级系统降阶，从而简化问题。

最后附上不同阻尼下的二阶闭环系统时域响应曲线。