SaberRD设计实例：DC-DC转换器的稳定性分析

1、前言

随着对直流电源需求的不断增加，通信系统、飞机、电动汽车等工业应用中相互连接的直流电源的使用也越来越多，这样一来系统的不稳定性风险大大加。单个电源有专用的反馈控制环路，在负载不均匀的情况下可能变得不稳定，同时网络中电源的并联或级联也会带来稳定性方面的挑战。因此，了解系统的稳定性变得至关重要。

本设计示例展示了一种确定由DC-DC转换器组成的系统是否稳定的方法。该方法基于传统的小信号交流分析，并使用转换器的平均非线性和非开关模型。

为了研究系统的稳定性，本例中使用了Middlebrook（米德尔布鲁克）准则。这里系统的稳定性可以通过测量源阻抗(zsource)和负载阻抗(zload)来确定。根据这种方法，如果|zload|>|zsource|，则系统是稳定的，如果|zload|<|zsource|，则系统是不稳定的。

阻抗测量仪器的位置对于确定互联DC配电系统的稳定性至关重要。只要违反了米德尔布鲁克准则就足以使整个系统不稳定。因此，从概念上讲，应该验证系统中的所有节点是否满足标准，并且当一个节点连接了两个以上的组件时，应该设想作为连接到该节点的负载集或源集的一部分的组件的所有排列。

实际上，要彻底检查的配置数量是很棘手的，需要进行工程判断来识别节点和最可能导致不稳定的源与负载分割。总线上最可能违反米德尔布鲁克准则的节点是距离为总线提供电源的转换器最近的节点。

对于该节点，通过将负载侧的所有下游负载和源侧的变换器馈电功率分组，可以获得最关键的分区负载与源负载的比值。有了它，所有负载的并联组合呈现最小阻抗，在仪器的负载侧可见；而在单个转换器的输出阻抗在源侧可见。

本例展示了SaberRD中使用通用组件库进行系统建模的能力，并在本例中证明了各种相关分析对系统稳定性研究的有效性。与其他仿真软件不同，使用MAST语言实现所需的功能(如测量阻抗)非常方便，使用Experiment Analyzer可以实现仿真过程的自动化，并以用户友好的格式创建结果。

本例中测试了两种电路拓扑结构。

1)单路DC-DC电源通过输入LC滤波器连接到直流母线上。

2)多路DC-DC变换器作为恒功率负载(CPL)的直流配电系统。

2、在SaberRD中建模

2.1. 带输入滤波器的单DC-DC电源

米德尔布鲁克准则旨在研究添加输入滤波器对反馈控制电源转换器的影响。图1所示拓扑是一个带输入LC滤波器的dc-dc降压转换器。

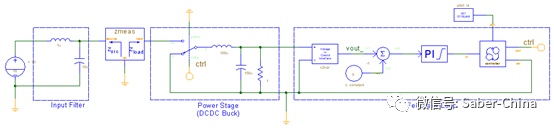
图 1 带输入滤波器的DC-DC变换器的稳定性分析原理图

下载后文提供的示例，从Single_DCDCconverter_stability_analysis文件夹中打开Stability_DCDCconverter_avg.ai_dsn设计，通过改变输入滤波器参数来确定它们对功率变换器稳定性的影响。除此之外，本设计还检验了改变反馈回路参数的影响。图1所示的拓扑中建模的关键子系统有：

1. 带输入滤波器的直流源：直流源为恒直流电压源模型。输入滤波器是一个LC低通滤波器，它的-3db带宽通过改变电感和电容的值来调节。
2. 阻抗测量模块：阻抗测量模块采用MAST语言建模，可用于计算源阻抗和负载阻抗。下面提供了zmeas模块的MAST代码。在直流和瞬态分析过程中，该模型只是实现了源和负载之间的短路，因此它对仿真结果没有影响。在交流分析过程中，它在偏置点的顶部注入一个小的信号电压扰动，从负载和源端都可以看到。由这种扰动引起的小信号电流在源端和负载端的阻抗都被测量。由于电压扰动幅值为1，其相位为0，因此所测电流与复阻抗Zload和Zsource直接匹配。注意，在交流分析过程中，内部交流电压源确保负载和源端之间的完全去耦(从小信号角度)，同时共享相同的大信号电压偏置点。

3. 功率级：采用平均无开关降压转换器模型来表示功率级(开关和整流二极管)。平均模型是基于80年代末Vatche Vorperian(米德尔布鲁克的学生)的开创性研究。它仿真速度快，同时提供了与完整交换模型良好的相关性。用户可以很容易地使用该模型来适应buck、boost、buck-boost或cuk转换器拓扑的开关要求。这有利于将注意力集中在稳定性分析上，而不是利用仿真器资源对功率变换器进行仿真。
4. 反馈回路：该拓扑结构采用了一种简单的闭环电压控制。控制算法驱动理想开关，理想开关输出与控制信号对应的直流电压。

2.2. 直流配电系统

下载后文提供的示例，从Stability_analysis_DC_distribution_system文件夹中打开DC_distribution_system.ai_dsn设计。

图 2 用于稳定性分析的DC配电系统原理图

本例中建立了直流配电系统的模型，以研究各种变流器之间的相互作用对稳定性的影响。Middelbrook准则适用于多转换器系统，方法是用功率转换器替换输入滤波器，并从充当电源的功率转换器处测量系统的输入和输出阻抗。

系统采用上节测试的dc-dc变换器。这是为了确保在互连系统中使用的各个块是稳定的。本设计演示了当多个电源连接到一个公共电源/电源转换器时直流配电网的稳定性。当直流母线保持在额定电压(在本例中为10V)时，无论负载侧发生什么，系统都是稳定的。在负载侧，每个电源同时接通，检查直流母线是否稳定。此外，阻抗测量还能显示每增加一个元件时系统的状态。

3、仿真与结果

在上一段中，我们展示了SaberRD在建模系统中的使用。各种模型的可用性和对用户定义函数建模的易用性使得在SaberRD中创建设计更加容易。

本节将详细介绍了在两种设计上执行的各种仿真，并对结果进行评估以检查稳定性。SaberRD配备了几个选项来了解系统的稳定性，如零极点分析、奈奎斯特图、阻抗测量等。本设计演示了使用阻抗测量来研究系统的稳定性。为了保证结果，需要：

1. 交流分析在系统的稳态条件下进行。
2. 为了使结果具有良好的相关性，应充分收紧截断误差。否则，数值积分的阻尼会虚构地吸收真实系统中可能存在的振荡。

3.1. 带输入滤波器的单电源仿真

先执行瞬态仿真以使系统达到稳态，然后运行小信号分析以获得频率响应。阻抗测量模块“zmeas”测量电源电压、电源电流、负载电压和负载电流。通过这些测量，可以计算出源阻抗和负载阻抗。通过检查阻抗波形来评估系统的稳定性。瞬态输出电压图还显示了系统的稳定性分析结果在时域和频域之间的良好相关性。

为了进行分析，改变滤波器电感值并评估其对稳定性的影响。当滤波电感影响系统稳定性时，改变电压反馈控制回路中的参数以提高稳定性。这由本设计中包含的两个实验来证明。

实验stability_analysis.ai_expt执行瞬态分析以使系统达到稳态，并在对应于瞬态分析结束的偏置点执行交流分析以获得频率特性。这是针对三个输入滤波器电感值进行的，以观察其对源阻抗和负载阻抗的影响。在zmeas模块中，使用AIM脚本(stability_analysis.aim)计算并绘制源阻抗和负载阻抗。一旦实验运行，所有的任务被一个接一个地执行，结果显示在图表中。

另一个实验是stability_analysis_feedback_gain.ai_expt。本实验将电压反馈控制环路的比例增益从1更改为0.1，并展示了这一更改对上一实验中所有输入滤波器电感值的影响。

3.1.1 运行实验进行仿真

1. 打开Stability_DCDCconverter_avg.ai_dsn设计
2. 按下图顺序操作，执行实验“stability analysis”。

3. 实验进度为100%后，进入SaberRD Tab，输入source stability_analysis.aim命令绘制图3到图5的波形图。

4. 要执行下一个实验stability analysis feedback gain，参考上面的2、3步绘制如图6到图8的波形图。

3.1.2 带输入滤波器的单电源仿真结果

aim脚本中还计算了zmeas块信号的源阻抗和负载阻抗。这使得分析图表和识别系统稳定性变得更加容易。

图3至图5显示了稳定性分析实验的结果

图 3 输入滤波器电感为1mH时的仿真结果显示不稳定状态

图 4 输入滤波器电感为1uH时的仿真结果显示显示边际稳定

图 5 输入滤波器电感为100uH时的仿真结果显示运行稳定

根据米德布鲁克准则，源阻抗必须小于负载阻抗。因此，从图3、图4和图5的图中可以看出，滤波器电感值越高，系统越不稳定。这也可以在转换器的输出电压上看到。

如3.1节所述，为了使系统在更高的输入滤波器电感值下也能保持稳定，还要进行额外的分析来优化转换器。图6到图8显示了运行稳定性分析反馈增益实验的结果。在这种情况下，电压反馈回路的比例增益从1.0更改为0.1，并进行相同的仿真。

图 6 降低比例增益和输入滤波器L=1mH的仿真结果

图 7 降低比例增益和输入滤波器L=100uH的仿真结果

图 8 降低比例增益和输入滤波器L=1uH的仿真结果

可以看出，通过调节电压反馈环路的比例增益，可以达到稳定。当输入滤波器电感L设置为1mH时，通过改变反馈回路参数，系统被调谐到稳定状态。因此，检查系统稳定性，并对设计进行必要的修正以提高稳定性。

3.2. 直流配电系统仿真

如图2所示，该设计有一个通用的直流电源连接到多个DC-DC转换器。通过依次增加电源来研究系统的稳定性。在这里执行与3.1节相同的分析，并检查系统的稳定性。

为了实现仿真流程的自动化，方便进行了实验稳定性分析，示例中提供了实验文件stability_analysis.ai_expt。实验仿真了每个电源的瞬态和交流分析。最后绘制了计算结果，验证了系统的稳定性。

3.2.1 运行实验进行仿真

1. 打开Stability_DC_distribution_system.ai_dsn.ai_dsn设计
2. 按3.1.1的操作，执行实验“stability analysis”。
3. 一旦实验进度达到100%，将由AIM脚本绘制图9和图10所示的图表，aim脚本是研究系统稳定性的实验的一部分。

3.2.2 直流配电系统仿真结果

图 9 直流配电系统仿真结果

图9所示的源zsource和zload负载阻抗比较表明，随着连接到总线的电源数量的增加，系统变得越来越不稳定。源阻抗和负载阻抗之间只有足够的裕度，最多4个电源。此后，系统趋于不稳定。

图10所示的10V直流母线电压曲线图清楚地显示了振荡和不稳定性。

图 10 负载增加时的瞬态分析波形

4、结论

本文详述了SaberRD用于研究了带输入滤波器和直流配电系统的直流电源的稳定性的过程。为了获得稳定性，使用Middlebrook准则测量输入和输出阻抗，并检查稳定性标准。测量阻抗和PWM控制器所需的模型可以使用MAST语言轻松建模。

在单路直流电源的情况下，输入滤波器阻抗影响系统的稳定性，通过调节控制参数可以提高系统的稳定性。因此，在保持系统稳定性的同时，可以根据所需的输入滤波要求进行设计优化。同样，在直流配电系统中，由于负载是随机的，评估稳定性是最重要的，示例清楚地显示了系统变得不稳定的情况，因此可以修改设计以提高稳定性。