请问Saber是如何将MOR电热模型转换为MAST模型的？

系统级仿真是产品开发的重要组成部分，这种仿真包括与设备模型相结合的电路组件。Saber是一种系统级仿真工具，开发中可以将MOR电热模型转换为MAST模型，并在Saber中进行电热仿真。模型简化在行业中被用于直接从有限元工具中获得紧凑模型。

本文概述了以下主题，并说明了在 Saber 中执行系统级电热仿真的方法：

※ 状态空间建模

※ 有限元分析

※ 模型降阶

※ 用于电热仿真的MOR矩阵

一、状态空间模型简介

在控制工程中，状态空间表示的是物理系统的数学模型，它由一阶微分方程相关的一组输入、输出和状态变量组成。系统的状态可以表示为该空间内的向量。为了从输入、输出和状态的数量中抽象出来，这些变量表示为向量。此外，如果动态系统是线性的、时间恒定的和有限维的，那么微分和代数方程可以写成矩阵形式。

线性系统

线性系统的最通用状态空间可以用以下形式表示，有M输入、R输出和N状态变量：

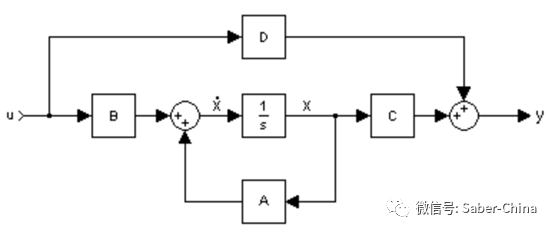
图1 线性系统的状态空间表示

A - 状态矩阵 A。行数与状态数相同的平方实值或复值矩阵。（n × n 矩阵，其中 n 是状态数）

B - 实值或复值矩阵，行数与状态数相同，列数与输入数相同。(n × m矩阵，其中m为输入数)

C - 实值或复值矩阵，其行数与输出数相同，列数与状态数相同。(r × n矩阵，其中r为输出数)

D - 实值或复值矩阵，输出行数和输入列数相同。(r-by-m矩阵)

E - E矩阵用于隐式(描述符)状态空间模型。默认情况下，e =[]，这意味着状态方程是显式的。为了指定一个隐式状态方程E dx/dt = Ax + Bu，将这个属性设为与a相同大小的方阵。

有关如何在不同域中派生的状态空间模型的一些示例，请参阅此链接。

二、有限元分析

有限元分析(FEA)是可用于求解偏微分方程的最强大的数值方法之一，它适用于复杂的形状。该过程将复杂形状细分为许多更简单的形状，在这些形状上可以轻松求解复杂的微分方程，然后将所有更简单的形状“连接”在一起，确保元素间边界的兼容性和平衡。该方法可用于结构分析、动力学、振动、流体流动、热力学、声学、静电学、电气和流体网络、电子学等。

热电应用是多样的而复杂的，通常需要一个完整的三维(3-D)数值分析。有限元法是求解PCB板热分布的一种有效方法。要应用有限元法，必须有以下方面的详细资料:

a. 设计PCB的几何形状。

b. 材料特性

c. 产生热量的位置和数量

d. 可选择的冷却类型和数量

通过定义整个信息，可以通过将其简化为数学关系来对实际问题进行建模。有很多方法可以对这个问题进行建模并研究PCB上的热量分布和散热。有限元模型是高维的，时间积分是不可行的。系统级仿真的常见做法是采用一个紧凑的或行为级的设备模型。这样的模型是低维的，但可以很好地逼近动力响应。MOR (Model Order Reduction),是一个软件，它读取系统矩阵，运行模型缩减算法，然后写出缩减矩阵。简化后的矩阵可用于制作Saber MAST和VHDL-AMS中的模板

三、模型降阶

模型简化或模型阶简化是一种数学理论，用于为常微分方程 (ODE) 系统找到低维近似。主要思想是高维状态向量实际上属于低维子空间，如图2所示。

图2 低维子空间的概念

在已知低维子空间的条件下，常微分方程可以投影到其上。图3显示了ode线性系统的情况。这个投影给了我们一个所需的低维近似。

图3 将一个ode系统投影到一个低维子空间上

对于热分析，简化的低阶系统作为瞬态热方程的状态空间表示给出，其状态向量为广义变量 z、演化矩阵 E 和 A、输入矩阵 B 和输出矩阵 C。矢量 TJ 包括所有晶体管结温。所需的状态变量数量由误差估计程序确定。

对于热分析，将低阶系统简化为瞬态热方程的状态空间表示形式，其状态向量为广义变量z，演化矩阵E和A，输入矩阵B和输出矩阵C。矢量Tj包含所有晶体管结温度。所需的状态变量数目由误差估计程序确定。

四、用于电热仿真的 MOR 矩阵

传统上，RC热网络是为瞬态热仿真而开发的。创建RC热网络的过程是半自动的。这意味着首先用户必须创建网络拓扑，这取决于热源的数量和结构的复杂性。然后，将传递函数参数与由有限元模型测量或计算得到的结构阶跃响应进行拟合，自动提取RC网络的参数。

使用模型简化可以更简单地解决热问题，因为传热偏微分方程的离散化会得到一阶常微分方程组。模型简化首先要用有限元程序创建一个精确的高维热模型。。

微系统内温度分布的 3 维传热方程示例如下：

这里，K是热导率，Cp是比热容，ρ是质量密度，T是温度分布，Q是发热率。

在空间上进行离散化，得到常微分方程组。

这里，-K 是由于附加的对流项，传导性矩阵从单纯传导热流的对称矩阵变为非对称矩阵，C是热电容（K和C是系统矩阵），T是离散化过程中节点处的未知温度，Fi是第i个热源对应的载荷向量，ui是输入函数，即第i个热功率如何随时间变化。

上述方程可以直接转换为类RC网络以用于联合电热模拟，但状态向量T的维数通常太高而无法在实践中利用这个机会。因此，首先应该推导出一个紧凑的热模型。

模型缩减的一个思路是找到一个低维子空间，以可接受的精度描述状态向量轨迹。

也就是说，假设误差向量å很小。矩阵V描述了从广义坐标z的低维子空间到未知温度的原始向量T的变换，它的列数等于低维子空间的维数。当找到子空间V时，投影得到低维常微分方程组。

这里

MOR4ANSYS 可用于自动生成降阶模型。它从ANSYS二进制文件中读取原始系统的系统矩阵，并执行Arnoldi算法以获得指定的最大阶数的简化模型。通过将结果与ANSYS 仿真进行比较来选择最佳顺序。结果是简化矩阵Kr和Cr、载荷向量Fr,i和变换矩阵V。

五、具体操作

1、将MOR矩阵转换为MAST模型

降阶热网络的演化：

我们可以将热MOR文件转换为Mast模型，其中状态空间公式 dX/dt=AX+BU 通常从 *.sml 文件中给出（已经进行了矩阵求逆）。

或者我们可以直接从MOR矩阵 mor.A、mor.B、mor.C、mor.E创建Mast模型，其中状态空间公式包括E矩阵，EdX/dt=AX+BU。本文采用这种方法。

输入向量U实际上对应于芯片上的有源器件产生的热流（而不是有源器件的温度）。有源器件的温度是状态空间公式的输出向量 Y (Y=CX)。

转换后的模型包括一个参考热引脚，该引脚将连接到提供环境温度偏移（例如 25°C）的本体温度源。

在此基础上，创建了脚本“mor”。要让此脚本生成 MAST 模型，需要设置以下输入。

※ MOR 矩阵文件

※ 模型名称

※ 输入端口列表

※ 输出端口列表

这些输入端口和输出端口的值通常可以在MOR矩阵给出的mor.B.names 和 mor.C.names 文件中找到。

2、将MOR模型转换为MAST的步骤：

第一步：下载 随附的mor.tlib和mor.tndx文件。

第二步：用A、B、C、E矩阵生成MAST模型的aim包。将上述两个文件复制到$INSTALL/lib/aim目录下。

第三步：下载并解压mor_model _example_simple.zip 文件。其中包含用于转换的“MOR_files”文件夹下的示例 MOR 矩阵以及用于电热仿真的 MOR 模型的仿真示例。

第四步：进入SaberRD命令窗口，运行以下命令，更改工作目录路径为MOR_files目录（cd D:/SaberExample/mor_model_example_simple/MOR_files）。

第五步：如下设置变量值并运行命令生成“mor_example.sin”：

设置模型 mor_example

设置输入 [list port1]

设置输出 [list port1 port2 port3 port4]

设置 E_file mor.E

设置 A_file mor.A

设置 B_file mor.B

设置 C_file mor.C

MOR:GenerateMAST **model **inputs **outputs **E_file **A_file **B_file $C_file

第六步：“*.sin”文件在 MOR 文件以给定名称保存的同一位置创建。检查模型是否存在任何差异。

第七步：为这个模型创建一个符号。

第八步：将此模型和符号复制到工作目录中，然后继续测试模型并进行电热仿真（在这种情况下，转换后的模型已经在测试文件夹中可用）。实际上示例“test_mor_simple.ai_dsn”和“test_mor_simple_electro_thermal.ai_dsn”已经提供，包含在“mor_model_example_simple”文件夹中以便理解。

第九步：将热流源或温度源相应地连接到每个端口并运行仿真以测试模型。分别使用提供的实验“test_mor_example.ai_expt”、“test_mor_electro_thermal.ai_expt”运行仿真并显示结果，如下所示。

第十步：你可以使用此aim包根据上述步骤从具有不同输入和输出数量的热MOR文件生成MAST模型。

3、使用降阶模型仿真节点处的温度

图4 测试 MOR2MAST 转换模型"test_mor_simple.ai_dsn原理图

在测试电路中，我们通过端口 1 将热量泵入网络。由于热网络在端口1有一个输入电阻，同时还有一些局部存储（分布式热电容），因此热量在整个网络中扩散，最终延迟到达其他端口并导致温度升高。

除了其他端口，热量还通过远处的环境温度散热片散逸，该散热片对应于FEA侧的恒温狄氏边界条件。这就是t_ref端口的作用，它充当温度偏移量。

如果我们不添加ref引脚，如果所有局部设备都是发热源，那么在这些节点处计算的温度将参考零而不是环境温度。一旦参考引脚连接到温度源，流经该温度源的热量就是通过边界表面辐射的能量。

图5 给定输入的测试模型结果

该模型现在可以与有源设备连接以运行电热仿真。该模型有 4 个热端口，其中一个用于连接代表 FEA 边界条件的环境温度源 (t_ref)。请注意，局部设备可以吸收或产生热量。像 MOSFET 或二极管这样的有源器件会产生热量。低于整体网络温度（包括环境温度）的散热器或温度源会吸收热量。您还会遇到没有明确的温度或热量驱动因素的情况。

MOSFET 或 IGBT 等有源器件根据器件中消耗的瞬时电功率 (v(t)*i(t)) 产生热量；这种热量将导致设备热连接处的温度升高，进而动态影响设备的电气特性及其产生的热量。电热系统成为一个闭环耦合，由仿真器解决逐次解决。

4、使用降阶模型来模拟电路应用中的结温的电热仿真

按照惯例，可以使用有源器件数据表中的 Zth 曲线来模拟结壳温度。环境温度升高的情况只能使用热模型来计算。

图6 PCB上有散热器的有源器件

图7 动态热MOSFET模型

动态热MOSFET模型允许自加热改变Rdson, Vth和其他温度相关的特性模型。这样可以实现闭环仿真，获得较高的精度。

下面的示例显示了用于检测给定应用的IGBT结温的仿真。通用 IGBT 模型是使用 SaberRD 的 IGBT 工具构建的。使用数据表曲线的 IGBT 模型也可以基于所使用的组件来构建。

该模型还提供了一个内置的 RC Cauer 网络来对数据表中的 Zth 曲线进行建模。仅使用 Zth 曲线的局限性在于它只给出了从结到外壳的温升，这里忽略了外壳到环境的温升。

图8 SaberRD的IGBT器件建模工具

下面的示意图用于使用和不使用 MOR2MAST 转换模型进行电热仿真，端口根据用于 FEA 的 PCB 模型连接。

图9 有和没有连接到IGBT的热MOR模型结果比较

热MOR仿真结果显示IGBT端口的温升高于没有PCB热模型的常规模型。这里MOR模型不能被解释为散热器，但可以是导致最坏情况温度的热源。

此示例是根据在线提供的随机矩阵创建的。它仅用于展示如何使用 MOR2Mast 转换模型连接回有源设备并使用Saber 进行电热仿真。