一文浅述电路系统中的谐振（中）

在上一篇中，我们建立了谐振电路系统的时域模型和频域模型，简单地分析了单管并联谐振电路实例中谐振网络的应用及其实现零电压（ZVS）开通的机理。在我的日常工作中，看到了有太多的同行对软开关概念及其实现方式非常感兴趣，但是一般的教科书本里的讲解只是在针对某个电路拓扑就事论事，各种公式，模态，图形看得让人眼花缭乱。这让很多从业人员望而生畏，不求甚解。所以今天这篇文章，我们就从软开关最基本的概念讲起，结合五个典型的电路，尽量避免复杂的公式推导，一起来看看软开关（特别是ZVS），究竟是怎么一回事儿。

一.什么是软开关

在对软开关基本概念做介绍之前，我们首****先看看硬开关在电路系统中存在的问题 。下面三张波形图及后文中全英文的图片引自南京航空航天大学任小永老师的 功率电子学 。

第1个问题：高频时的开关损耗问题

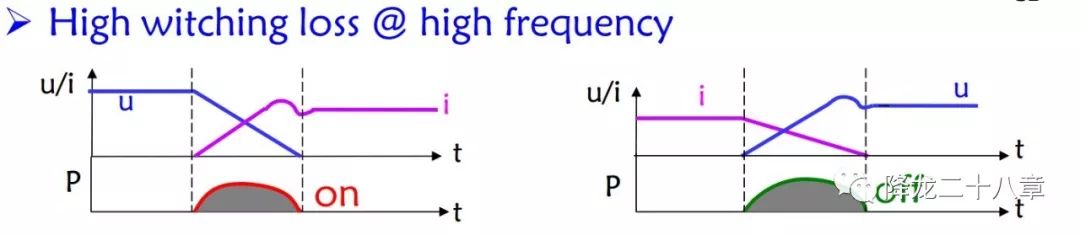
以IGBT为例（下文同），硬开关的开关过程中，器件Vce电压与沟道电流Ic(图中分别用u，i表示）的交叠时间内产生的损耗能量全部转化成了器件半导体芯片的热能，并且器件的损耗功率与开关频率成正比。因此当开关频率推向高频时，硬开关带来的开关损耗变大，器件温升变高，可能使得器件芯片结温超过规定的最高温度产生失效。

第2个问题：器件的安全工作区问题

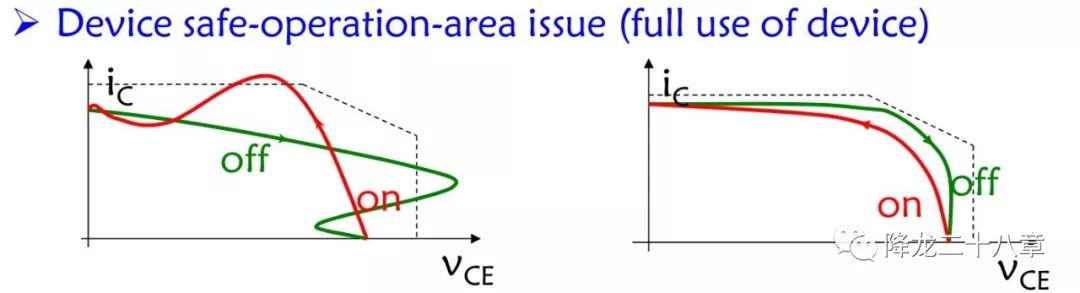
硬开关过程中，如果线路中的寄生电感电容参数较大，器件在开关过程容易发生振荡，使得其电压电流应力超过器件允许的安全工作区。为避免这一安全隐患，器件必须大幅降额使用，从而使得器件的利用率低（例如本来100V输入的场合，VDS产生了200V的震荡尖峰，就必须使用至少300V耐压的器件），这样就增加了器件的成本。

第3个问题：电磁干扰（EMI)问题

在硬开关过程中，器件的Vce电压的变化斜率dv/dt和Ic电流的变化斜率di/dt，都会给电路系统带来EMI噪声。这里我们不做过多的叙述（之前有读者希望我能写这方面的内容，但其实我也没有太多经验，不能误人子弟啊）

为了实现避免硬开关带来的这些问题，软开关技术应运而生：

如下图， 在Vce电压降到零后再开通器件，是零电压开通；在Ic电流降到零后再关断器件，是零电流关断 。图中驱动电压未给出，读者自行思考驱动波形。

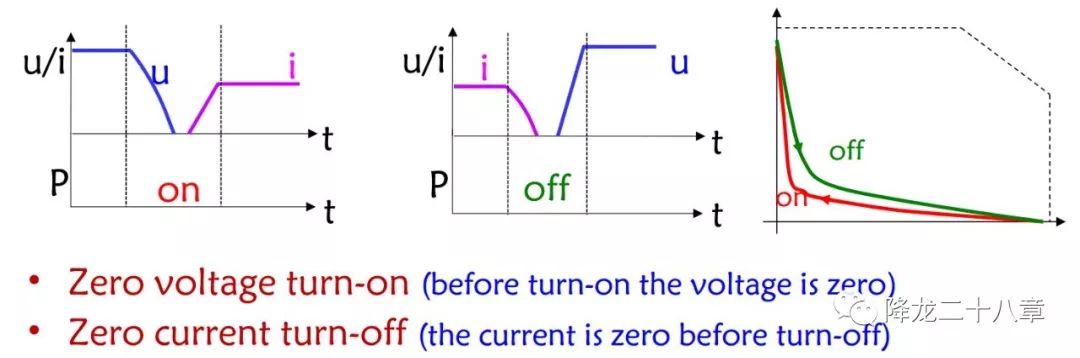
这里，我们需要知道， 软开关是一种技术， 包括 零电压开通（ZVS） 技术和零****电流关断（ZCS）技术 ，是为了优化电路某些方面性能而产生的技术，并不是一个具体的电路，更不是指某种特别的开关。

那么，怎样实现这个技术呢？

搭配谐振网络去实现。

上一篇我们提到的单管并联谐振电路就是一种实现方法。今天我们 再继续详细介绍几种零电压开通（ZVS)的实现方法 （零电流关断的方法请感兴趣的读者自行查阅相关资料）。在此之前，我们先看一些软开关技术的尝试，这些方法并未真正实现软开关，但可以给我们提供一些思路，我们姑且称其为弱化版的软开关技术。

二.弱化版ZVS技术

例1.Boost电路的断续模式

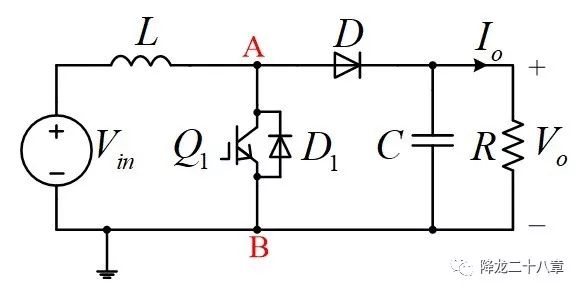
这里，我们考虑最基本的电力电子电路之一，Boost电路。其中Q1为IGBT，D1为与IGBT合封的二极管，我们知道，根据负载电流的大小和开关频率等条件，Boost电路可以工作在 连续模式、断续模式、临界连续模式 。在断续模式，Boost电路一共有三个模态：

模态1,开关管导通，电源电压直接加在电感L两端，电感电流上升，电感储能，此时开关管两端电压Vce=0（忽略饱和压降）

模态2，开关管关断，由于电感的能量不能突变，电感电流只能改变流通路径，转向二极管D的那条支路，迫使二极管D导通，给电容C充电的同时给负载提供能量，此时电感两端电压翻转变为负压（Vin-Vo<0)，电感电流下降，开关管两端电压Vce=Vo(忽略二极管压降）

模态3，由于电路工作在断续模式，电感电流下降至零后，一个开关周期还没有结束，此时会发生什么呢？

当电感电流降至零后，电感储能为零。此时似乎再没有电流传输路径了，但我们要考虑到，实际的开关器件都不是理想的开关，而是带有一定寄生参数的。这里，我们需要考虑到IGBT的结电容Coes和二极管的结电容Cd，此时电路模型变成下图：

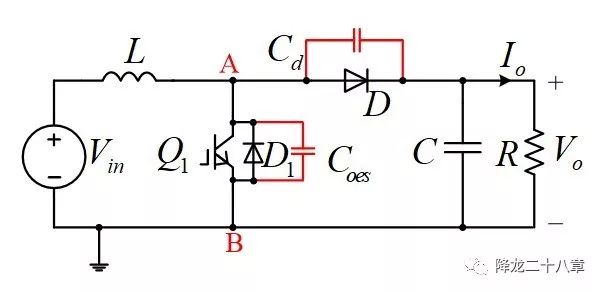
在一个开关周期内，输出电容C上的输出电压可以认为是不变的，因此可以把C及R等效为一个直流电压源。可以简化得到此时的谐振网络如下图

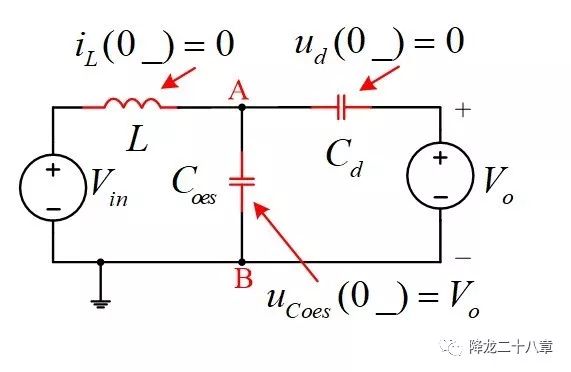
其中iL(0_),ud(0_),ucoes(0_)分别为电感电流刚下降至零时的状态量。这样，我们就可以用上一篇中提到的频域的方法或时域的方法求解模态3的Coes两端电压。根据图中的模型，我们得到的Coes两端的电压振动必然是一个谐振动，因为上面的模型没有考虑到线路中任何的寄生电阻。

当我们把各个元器件及线路的寄生电阻加上后，则电路模型可由下图表示。图中，R1，R2，R3分别为电源支路，开关管支路，二极管支路的等效寄生电阻。 这个电路模型才是符合实际的阻尼振动模型 ， 开关管寄生电容Coes的初始能量被逐渐消耗 ，如果开关周期足够长，那么最Coes两端的电压就会达到一个稳定值，这个稳定值即为输入电压Vin，二极管D两端的电压同样会稳定在Vo-Vin这个值。

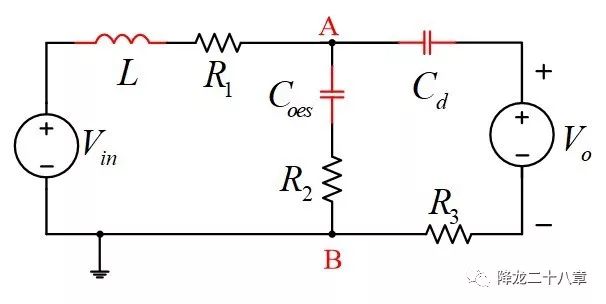
那么，我们能否利用这个电路断续时的谐振过程，去实现软开关呢？

很遗憾，答案是否定的。因为结电容中的储存的能量实在太小，不足以使得IGBT的VCE电压再次谐振到零。

但是我们可以退而求其次，找到一个与软开关接近的近似的解--谷底开通。在阻尼谐振过程中，当IGBT的Vce谐振达到谷底时，我们再开通IGBT。 在IGBT开通前，Vce电压被大大减小，虽然此时仍然是硬开关，但硬开关带来的损耗温升EMI问题都被大幅减小 ，何乐而不为呢？

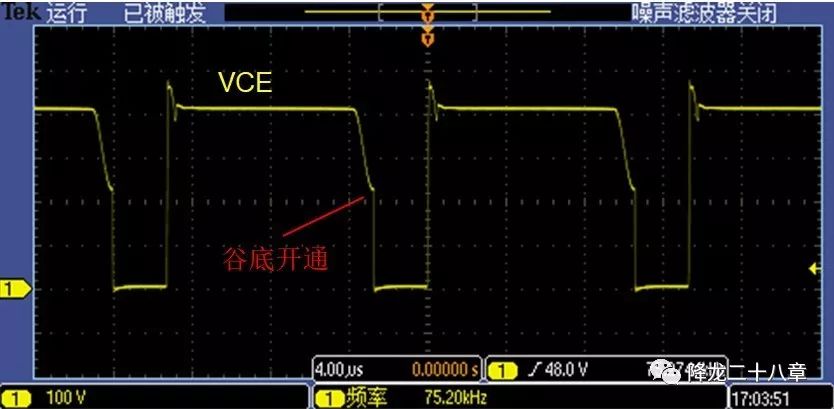
谷底开通技术被广泛使用在另一个基本电力电子电路中---反激(Flyback)电路。接下来，我们来介绍Flyback电路中的谐振。

例2.反激电路的断续模式谐振

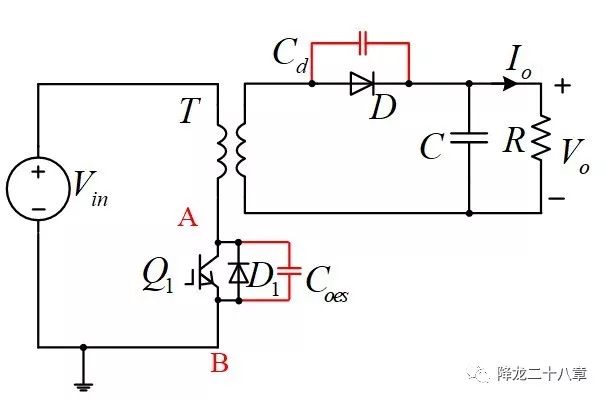
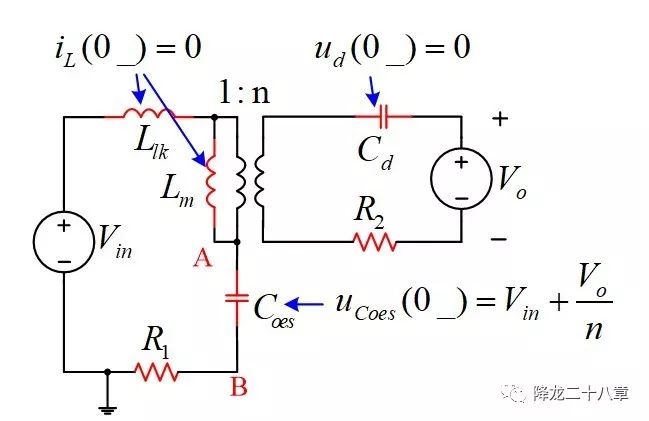
同样考虑反激电路的断续工作模态3：与Boost断续模式类似，上一个模态结束时，变压器中储存的能量刚好释放完，二极管D续流刚好结束，副边电流为零。此时输出电容及负载，副边二极管结电容Cd，原边开关管寄生电容Coes，变压器T，输入电压源，组成谐振网络如下：（考虑了线路中的寄生电阻，并应用变压器的漏感模型，同时忽略变压器的层间电容，匝间电容等寄生参数）

将图中变压器二次侧的电路折合到原边，则可得到如下模型：

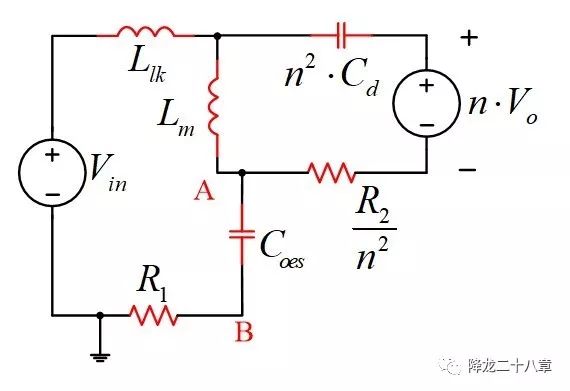
针对该模型，我们同样可以用上一篇中的频域方法，得到Coes电压的解析表达式。值得注意的是，电路模型中Coes和Cd都是随开关器件两端电压变化而高度非线性变化的，不能看成常数。篇幅有限，这里我们不做太多的运算推导，直接给出一张断续反激的Vce电压（实际是Vds)波形，让大家对这个谐振过程有个直观的认识。

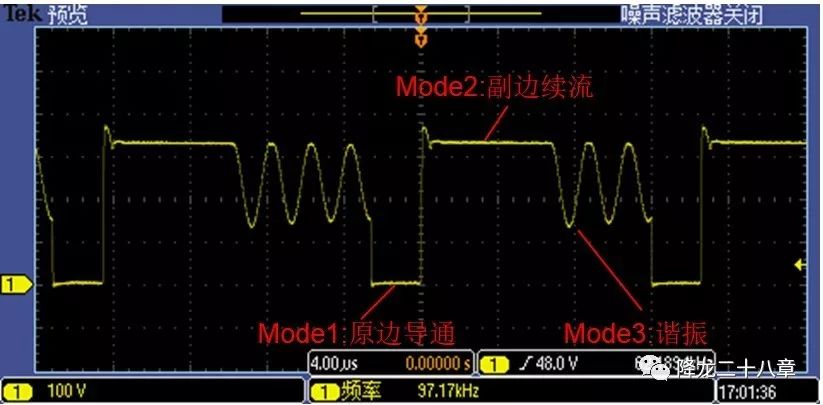
从上图可以看到，每个周期的开通点都在谐振波形的谷底处，这样大大减小了开通损耗。这种控制方式叫准谐振控制，是提高反激变换器效率的重要手段，其关键点在于寻找谷底。谐振过程是一个阻尼振动过程，选择第几个谷底作为开通点，则需要综合考虑输出电压稳压和输出功率连续调节，这里我们不做过多阐释。

总结前文中的两个电路，我们可以看到，为了实现零电压开通，必须想办法把IGBT器件的Vce电压降到零。如果谐振的初始能量不够，则难以通过谐振将IGBT的电压降到零。至此，我们找到了实现ZVS的第一个条件，足够的谐振能量。

接下来，我们来看ZVS的第二个条件。

三.感性换流支路

我们知道，电感电流不能突变，是指电感的储能是连续的。当线路中电感电流存在两条通路时，电流必定是先走阻抗更小的支路。但是当这条阻抗小的支路被阻断时，例如该支路中存在的有源器件被关断，为了维持电感能量的连续，那么电感电流只能通过另外一条支路流通。我们的基本电力电子电路，包括BUCK电路、Boost电路等，都是利用了这个思想。

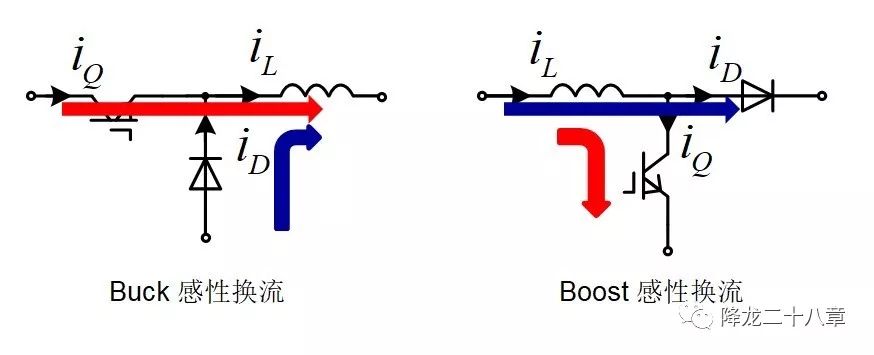
实现ZVS的器件，都是双向器件。所谓双向器件，即电流既可以从沟道 正向流通 ，也可以通过其寄生的 二极管 （或者IGBT合封二极管、或者外部并联的二极管）负向流通。

当器件的Vce电压（或Vds电压）被外部谐振手段降到零后，感性能量强制使得并联的二极管导通，此时器件的Vce电压被箝位在二极管的正向导通压降（可以认为是零），在并联二极管导通的过程中开通器件，即实现了器件的零电压开通（ZVS）。

我们以下图为例说明：

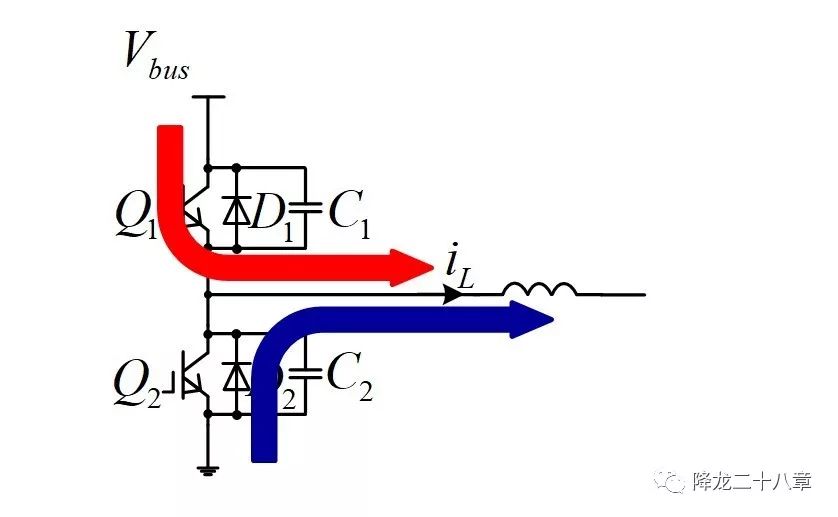
初始状态，Q1开通，Q2关断。正向的电感电流只通过Q1沟道导通（Q1沟道阻抗小)，当Q1关断，则可以通过谐振网络（图中没有表现出来）的方法，使得Q2的寄生电容C2的电压从Vbus降到零。这时，由于Q1已经关断，电感电流需要寻找另外一条路径导通，显然只能从Q2的并联二极管导通。在D2导通期间，给Q2发驱动信号，开通Q2，即实现了下管Q2的ZVS。

可见， 要实现ZVS，需要感性换流后开关管并联的二极管流通电流 。接下来我们再举几个实现了ZVS的电路例子，并分析第三个条件。

四.ZVS电路实例

前文中我们提过，需要谐振网络配合去实现软开关。这里，我们列举几个将谐振网络应用到电路中实现ZVS的例子。

1.半波准谐振ZVS

大家不要被这个奇怪的名字吓倒， 本质上这个电路是PWM电路和谐振电路结合的典型实例 。值得注意的是，这里的准谐振和反激电路的准谐振是两个概念，请不要混淆。相信大家已经有了PWM电路的基础后，再结合我前面所讲解的，来看这个电路会比较简单。（有兴趣的读者可以对比这个电路和我们上一篇中的电磁炉电路）

这个电路的拓扑图，模态分析及简单描述在下面图片中（同样引自南航任小永老师的PPT），这里我们还是针对这个电路详细分析。

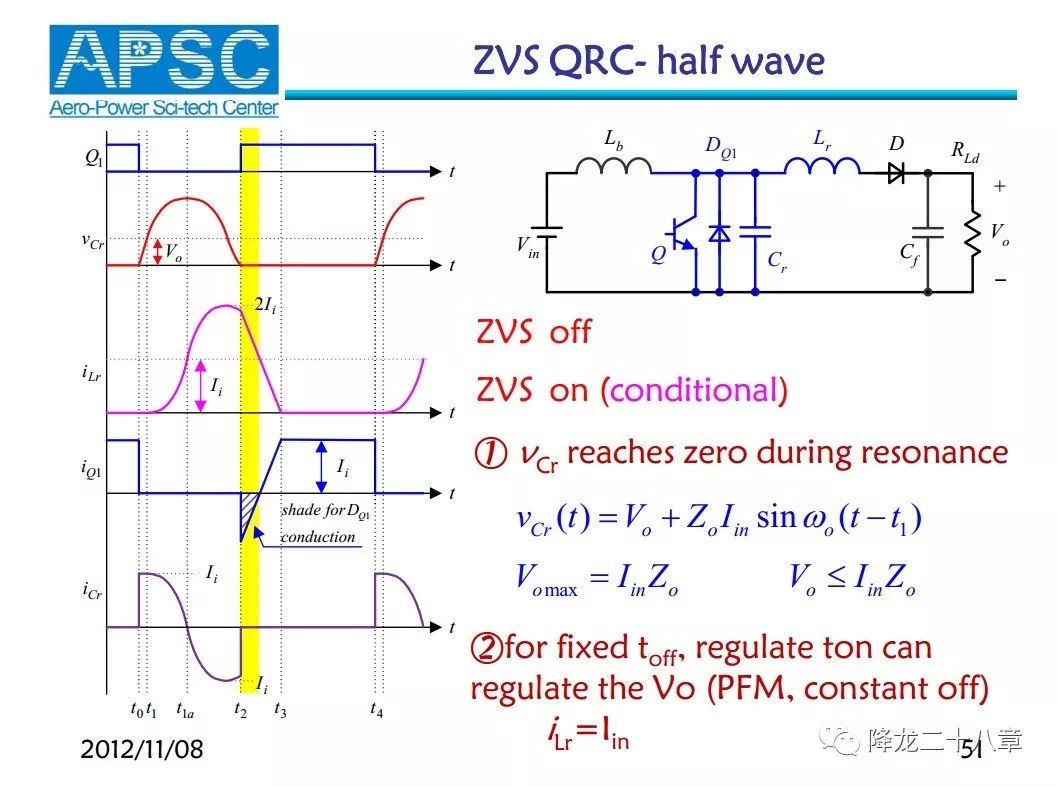
模态1，t0-t1：t0时刻，开关管Q刚关断时，谐振电容Cr的电压为零，谐振电感Lr的电流为零（这表示此时的谐振网络中没有初始能量），Cr电压远低于输出电压，二极管D处于截止状态。但此时电源的能量通过输入侧的大电感Lb（输入可以看做电流源），逐渐储存到谐振电容中，谐振电容电压Vcr被抬高，直至Vcr=Vo;

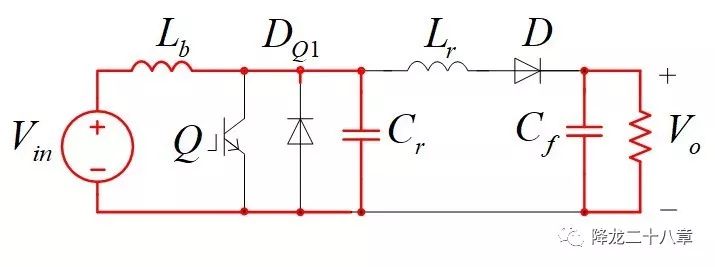
模态2，t1-t1a：t1时刻，谐振电容电压与输出电压相等，二极管D开始导通，此时，谐振网络形成，其等效电路如下：

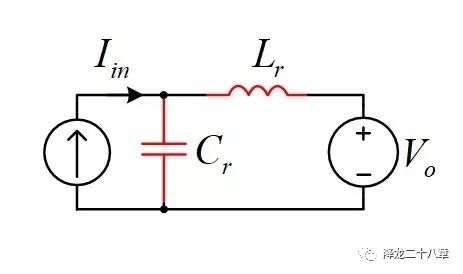
可以看到，虽然电路拓扑元件数较多，模态复杂，但是谐振网络形式却非常简单。模型中谐振电容的初始电压ucr(0_)=Vo。（ 感兴趣的读者可以写出此时电容电压和电感电流的表达式 ，作出其波形）。经过1/4的谐振周期后（t1a时刻），谐振电容电压达到最大值，谐振电感电流达到输入电流Iin。

下图为模态2与模态3的电流流通路径图

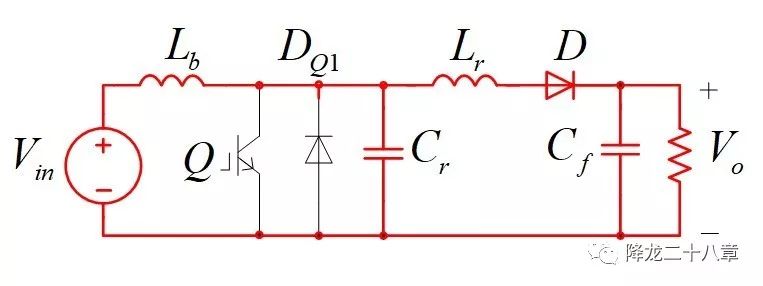
模态3，t1a-t2：谐振过程继续进行，此时的谐振电容电压开始下降，如果谐振能量足够大，谐振电压振幅大于输出电压Vo，则可以将谐振电容电压Vcr降至零。注意到，谐振电容与开关管Q并联，谐振电容电压降到零，意味着开关管Q的电压降到零。

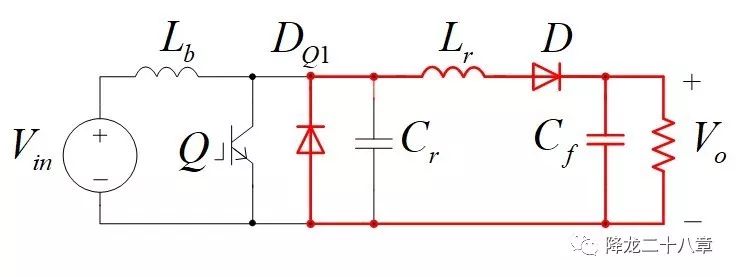
模态4，t2-t3：t2时刻，Vcr电压降到零，电感电流需要换流，从那条支路换？----二极管DQ1支路。 在二极管DQ1流通电感电流的过程中开通Q1时，便实现了ZVS。 那么，这个二极管导通过程持续多久呢？二极管DQ1导通后，谐振电感Lr两端电压被箝位在了输出电压Vo,故电感电流会线性下降。而谐振电感电流由两部分组成，输入电流Iin和二极管DQ1电流Idq1相加（KCL定律）。输入电流可以认为是恒流，所以二极管DQ1电流也是线性下降的，下降的斜率由输出电压Vo值和谐振电感感量Lr决定。这里我们先埋个坑，请读者思考：如果错过了二极管导通电感电流的时机，在二极管续流结束后再开通Q，会发生什么？

模态5，t3-t4：当谐振电感电流下降至零后，谐振网络中的能量全被传送到了输出侧。此时谐振电容电压为零，低于输出电压Vo，输出二极管D截止，谐振网络自然断开，输出与输入脱离。开关管Q已导通，输入电流通过开关管Q导通，为下一个周期的谐振做准备。

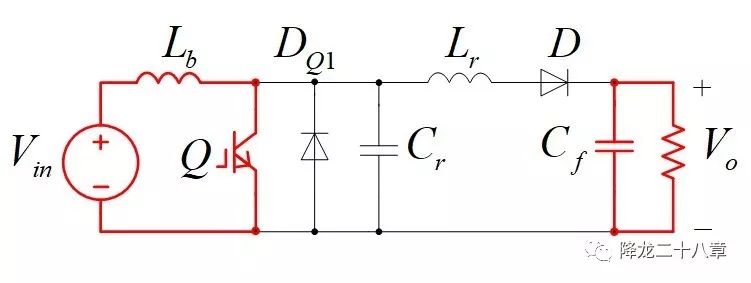
以上就是这个电路的模态分析。

这里，我们看到了前文中提到的实现ZVS的两个条件：

1）足够的谐振能量，使得谐振能将开关管Q的Vce电压降到零，在这个场合表现为谐振电压振幅必须大于Vo。

2）换流支路，DQ1必须存在。

接下来我们结合上一篇中提到的电磁炉并联谐振拓扑阐述 第三个条件 ：合适的开通时机。

2.单管并联谐振拓扑

上一篇中，我们提到了电磁炉应用的单管并联谐振拓扑，简单地介绍了其四个模态，并介绍了其ZVS实现情况。现在，电路参数设置已经满足了以上两个条件（能量和换流支路），下面我们来关注这个电路的ZVS实现情况。

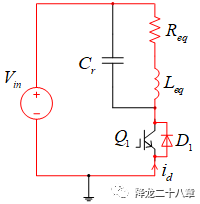
1）下图是正常ZVS时的情况，当Vce电压（蓝色）等于零时，开通器件，ZVS ON，橙色是IGBT电流，负值表示电流通过二极管流通，正值表示通过IGBT沟道流通。n_17为驱动信号。

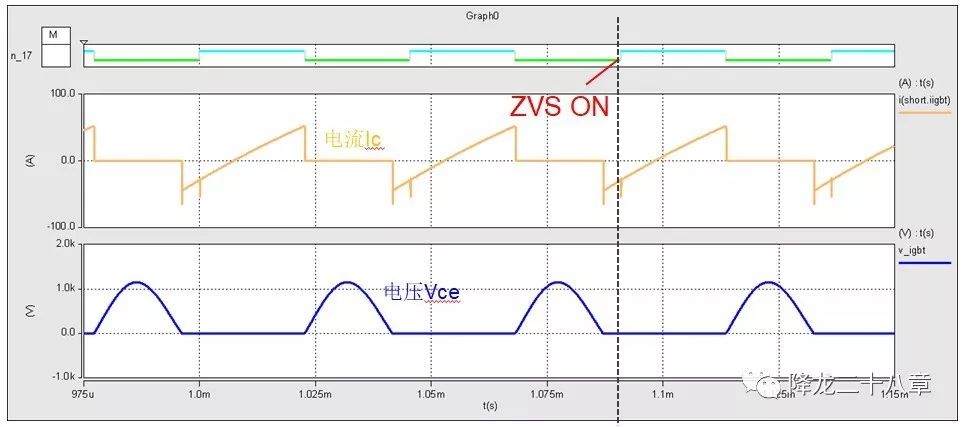
2）下图是未实现ZVS的典型情况，由于在二极管续流阶段未及时开通IGBT，导致谐振电容电压再次起振（阻尼振动），Vce电压不再为零，从而失去了实现ZVS的条件。

这样，我们可以看到， 实现ZVS，还需要找到合适的开通时间点 。

至此，我们阐述了实现ZVS的三个条件，不知道大家对软开关ZVS这种现象是否有了更深刻的理解呢？

我们回顾上文中列举的两个电路案例，其感性电流的换流情况都是 从外部谐振电容支路换到了二极管支路 。下面，我们再举一例从****开关管沟道换流到二极管支路的情况 。

3.移相全桥ZVS电路

移相全桥电路是电力电子技术中大功率场合的常用拓扑。四个功率半导体组成的桥式电路，既可以用于恒压输入场合，也可以用于恒流输入场合。在恒压输入场合，桥式电路使用移相控制的方式，能很方便地获得ZVS的条件。接下来我们针对这个电路做一点简单的分析。（这里我们还是引用任老师的PPT）

为了简化问题，我们只关注****两个关键模态 。

第一个关键模态如下图。

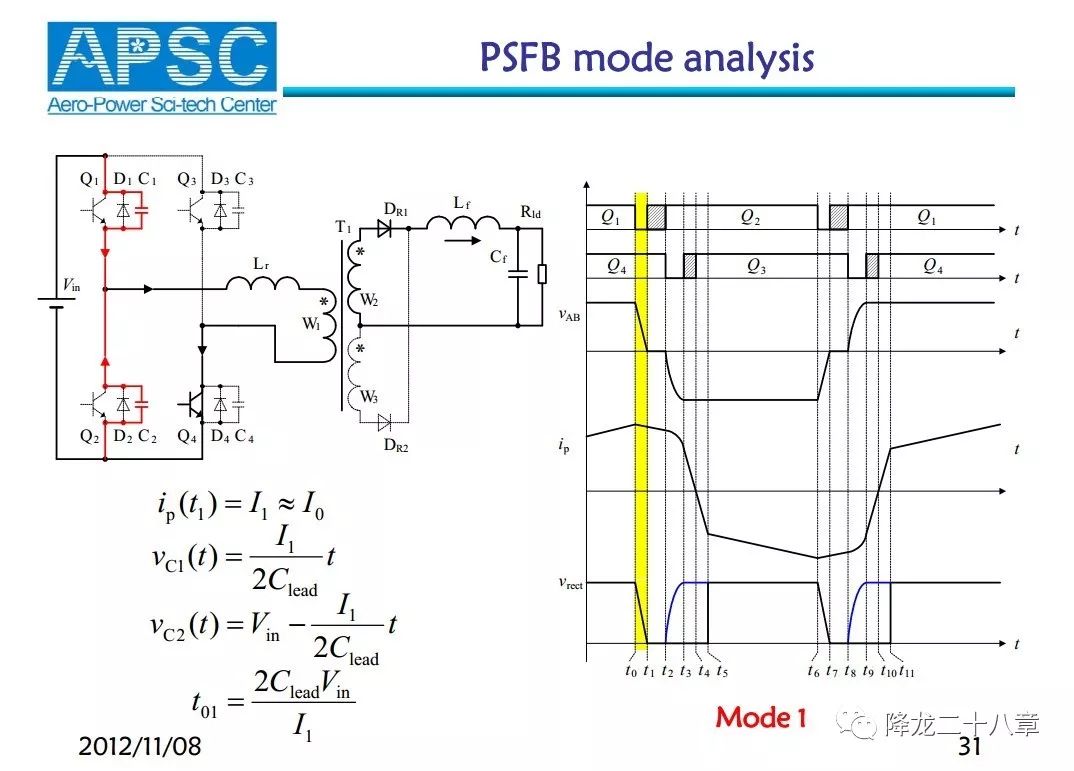
这个模态是指，Q1关断后，四个开关管中只有Q4的驱动电平为高，即只有Q4的沟道是导通的（在此之前，感性电流通过Q1和Q4的沟道流通）。此时由于电感Lr还在流通感性电流，这个感性电流迫使Q1和Q2的结电容充放电（本质上还是一个谐振过程，但电感能量相对电容能量大很多，故可以将电感电流看成恒流源），使得Q2的结电容的电压从Vin下降至零。只要Q1关断前电感Lr的电流足够大，那么Q2结电容电压必定可以被拉到零。此后，感性电流再通过Q2的并联二极管D2导通，提供了实现ZVS的条件。

我们把Q1，Q2所在的桥臂成为超前桥臂， 超前桥臂实现ZVS是相对容易的，因为此时原边还在向副边传递能量，电感电流与负载电流满足变压器变比关系，本质上谐振能量是来源于负载（可以等效成恒流源折合到原边）。 所以对于电压型移相全桥电路而言，重载更容易实现ZVS。

第二个关键模态如下图

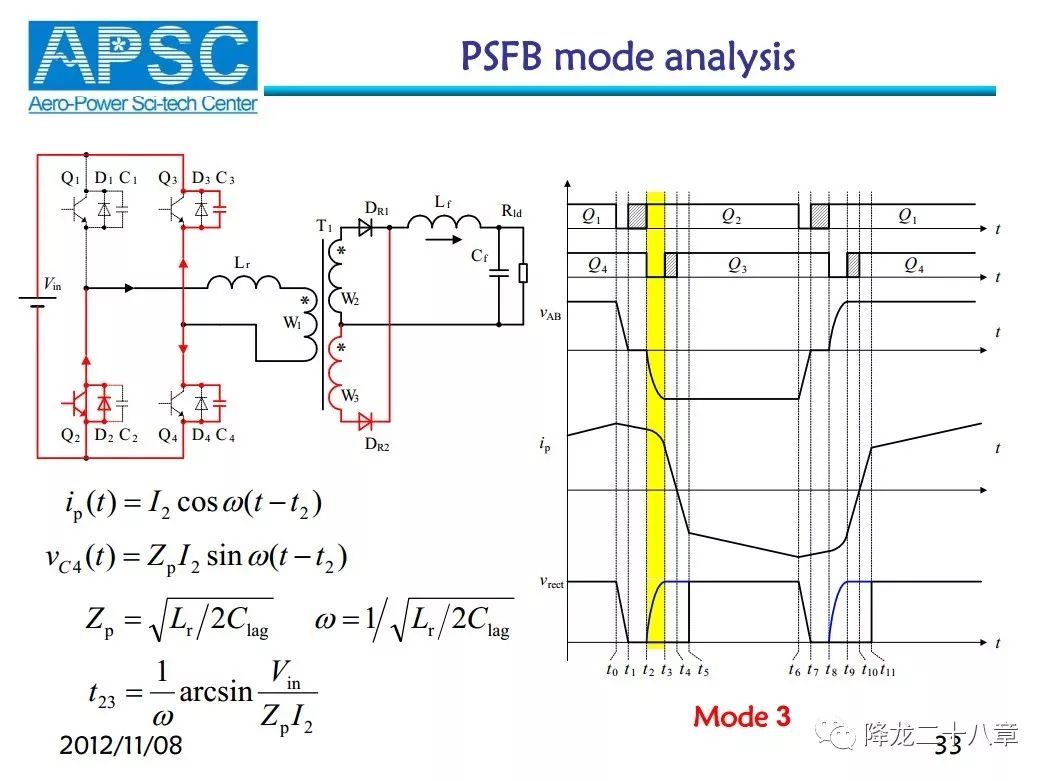
这个模态是指，Q4关断后，四个开关管中只有Q2的驱动电平为高，即只有Q2的沟道是导通的（在此之前，感性电流通过Q2和Q4的沟道流通，两个桥臂中点电压为零）。此时由于副边的二极管还处于换流阶段，副边两个二极管同时导通，变压器被短路。所以谐振网络是谐振电感Lr及C3，C4的两个结电容，谐振能量完全来源于此时电感的储能。如果能量足够大，便能将C3的电压降至零，从而D3导通，完成ZVS。但更多的情况是此时的能量不足，Q3依旧是硬开关。

Q3,Q4所在的桥臂称为滞后桥臂，滞后桥臂实现ZVS是不容易的，因为他们实现ZVS的能量来源是电感Lr的初始储能，没有依靠负载的能量。

以上移相全桥电路的例子，就没有利用外部的谐振电容，只是利用了开关管的寄生电容和变压器漏感（谐振电感)，并且感性电流从沟道换流到了寄生电容再换流到二极管，同样也能实现ZVS。

总结：

至此，我们一共列举了五个例子来阐述软开关ZVS与谐振的关系。

第一部分我们提到了Boost电路的断续状态和断续反激电路的准谐振控制，第二部分提到了给出了感性换流的概念，第三部分给出了真正实现ZVS的三个实例，包括半波准谐振ZVS电路，单管并联谐振电路和移相全桥电路，提炼出了实现ZVS的三个条件：

1）足够的谐振能量；

2）感性换流支路；

3）合理的开通时间点。

希望本文的梳理能让大家对软开关（特别是ZVS）这个概念有更深入理解，并将其应用到其他电路实例中，那么这篇文章的目的就达到了。