一文浅述电路系统中的谐振（下）

前两篇中，我们介绍了谐振电路系统的时域分析方法和频域分析方法，并结合了不同的电路实例，总结了软开关ZVS的实现条件。我们的思路是从最基本的电力电子电路出发，逐步将谐振和软开关的概念引入到PWM电力电子电路中，所以我们重点关心了电路的模态和波形等时域表现。我们从直观上对时域的模型更熟悉，但从电路分析的角度，模态和波形分析只是在某一个具体的频率条件下进行的。

对于谐振电路而言，如果只了解电路的时域表现，就仿佛是只看到了冰山一角 ，和频率相关的大部分知识都藏在海底。而今天我们需要做的，就是要让剩下的冰山，全部浮出水面。

一.再论欧姆定律

大家可能觉得很奇怪，欧姆定律这种初中生就知道的常识，为什么还要拿来这里说。这里，我们讨论的欧姆定律，不再从时间的角度考虑，而是从频率的角度考虑，它描述的是电压和电流的一种线性关系。比如，在直流稳态电路中，我们知道，要计算某段导体的电阻，只需要用这段导体两端的电压除以流经导体的电流即可得到。

那么，当我们在这段导体上施加的电压是交流电压，而且电压是以正弦波的形式交变，我们还能得到相同的结论的吗？如果把这段导体认为是理想的纯电阻，答案是肯定的。施加频率为f1的正弦波电压，就得到频率为f1的正弦波电流；施加频率为f2的余弦波电压，就得到频率为f2的余弦波电压。在任何频率下，电阻两端的电压都与流经电阻的电流成正比，这个比例系数，就是电阻值。

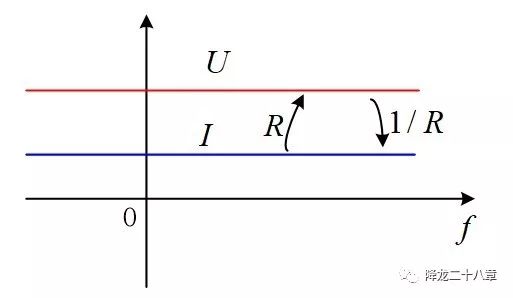
这样，在整个频域，电压和电流形成了一种映射，而且是一种线性映射，这就是欧姆定律在频域的本质。

但是实际上，任何导体都不可能是理想的纯电阻。

当我们把两端正弦波电压频率增高（比如到了100MHz），我们会发现流经导体的电流的相位和施加的电压相位有些偏差，学过电路理论的人应该都知道这是由于导体的高频感抗造成的。

在一些电工学的教材中，正弦稳态分析和阻抗的概念被引入。把电压和电流当做旋转矢量这种方法，与我们第一篇提到的简谐振动旋转矢量类似。

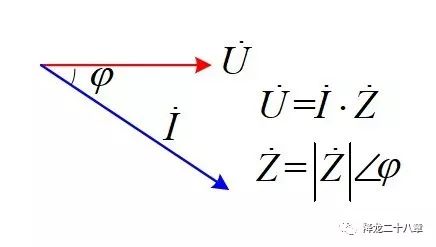
但稳态意味着只在某个频率点，我们之前提到，电力电子电路中存在大量的开关动态，一个开关（阶跃）动作，就意味着无数多个高频激励分量。这样，正弦稳态分析的方法不再适用，我们需要找到更广义的解法--频域阻抗。

在频域中，我们假定存在这样一个激励：激励电流Iin(f)=1，即激励电流由无穷多个频率下的单位激励合成，如果我们想要关心电路系统在任何频率下的电压响应，那我们就需要一个关于频率f的阻抗函数，这个阻抗函数不仅要包含在各个激励频率下的电压电流幅值的比例系数信息，还要包含了各个频率下电压电流的相位差信息。

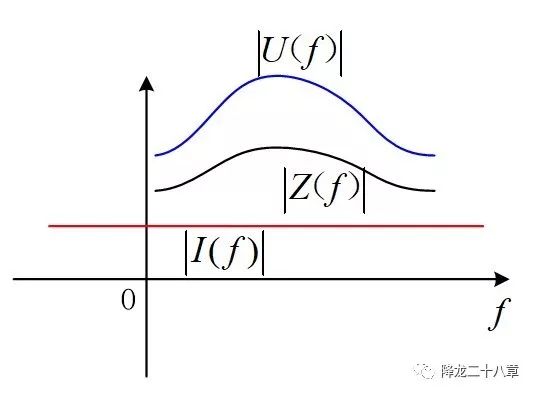
因此，我们需要引入频域阻抗（或者复阻抗）的概念。如果说正弦稳态分析中的阻抗是海面上我们看得到的冰山，那整个频域的频域阻抗就是包含了海底部分的整个冰山。

频域中，电感的阻抗和频率成正比，这是由电感的充放电关系决定的

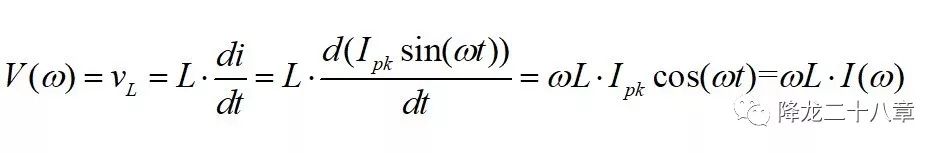
电容的阻抗和频率成反比，这是由电容的充放电关系决定的。

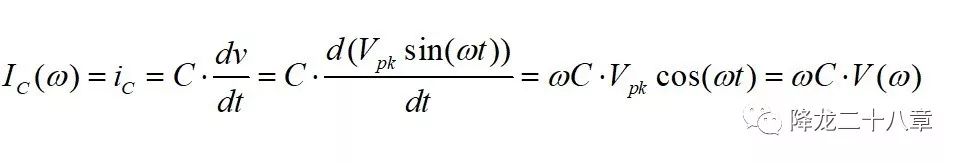
我们知道，谐振网络主要是由电感、电容和电阻三种元器件组成，这样我们可以把谐振网络等效成一个线性二端口网络。

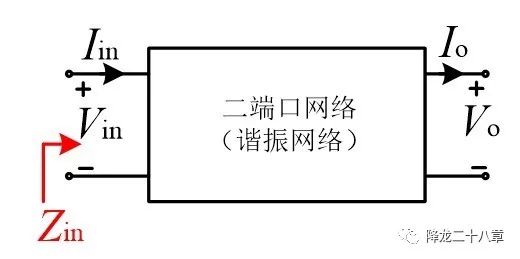
二端口网络的左侧认为是输入侧，一般接能量供给单元，例如电压源，电流源等，右侧认为是输出侧，一般接能量消耗单元，例如电阻（或者等效的电压源，电流源）。当负载接入后，从左侧看过去，可以认为输入电流和输入电压满足一定的函数关系：

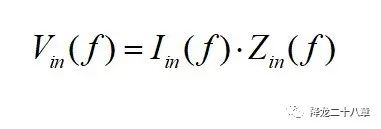
这里的Zin(f)即为这个二端口网络等效的输入阻抗。它反映了特定负载条件下，施加不同频率的激励（可以是电压，也可以是电流），二端口网络从输入端表现出来的外特性。

怎样量化这个阻抗呢？

从电路的频域模型入手。

比如一个简单的LCR网络，容易得到其频域模型，令初始状态为零，可以得到从输入电流到输入电压的传递函数。只需要将传递函数中的s，代换成2πjf,这里的f是频率，j是单位虚数。

这样根据频域模型得到的传递函数便有了物理意义，它表示系统在各个频率点的输入阻抗Zin(f）。各个频率的输入阻抗Zin(f)都是复数，它的幅值规定了输入电压幅值和输入电流幅值的比例，幅角定义了该频率下输入电压超前于电流的相位角。

二.正弦波等效分析

前文中我们讲到了谐振网络的输入阻抗概念，接下来我们便要将这个概念应用到谐振变换器中。以串联谐振DC/DC变换器为例，下图是该变换器的电路拓扑。

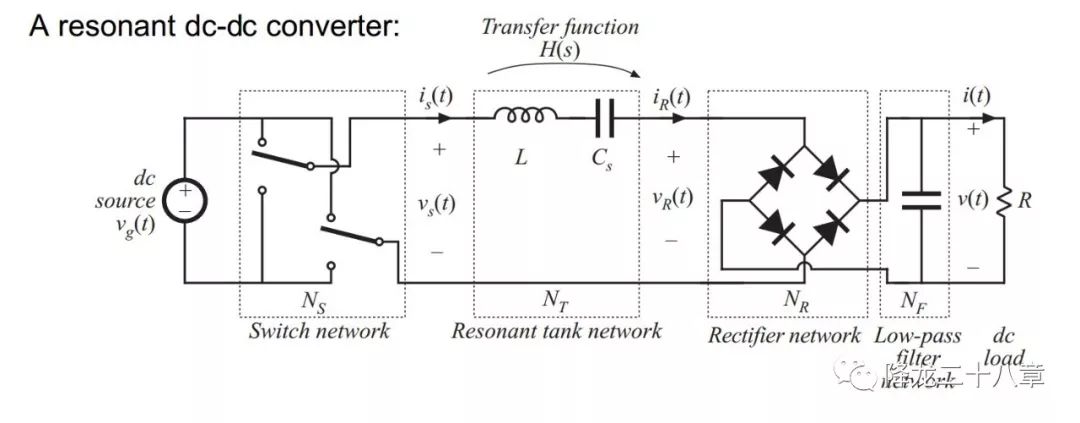
这是一种典型的谐振变换器电路，电路由四个二端口网络构成，开关网络，谐振网络（或者称谐振腔），整流网络，滤波网络。

从传递函数的角度来看，开关网络和整流网络都是含有开关器件的非线性网络，而谐振网络和滤波网络则是线性网络。我们的目的是要从频域分析整个电路的特性，所以对各个网络做单独的等效处理，将所有的非线性网络等效成线性网络。

首先关注开关网络。由于输入电压源的存在，开关网络的输出电压为方波电压。同时谐振系统具有选频特性，可认为谐振腔只对谐振频率的激励进行响应。 所以我们不妨假设开关网络的开关频率接近谐振频率 ，这样开关网络的方波输出电压中只有其基波分量被响应，其他频次分量都可忽略。

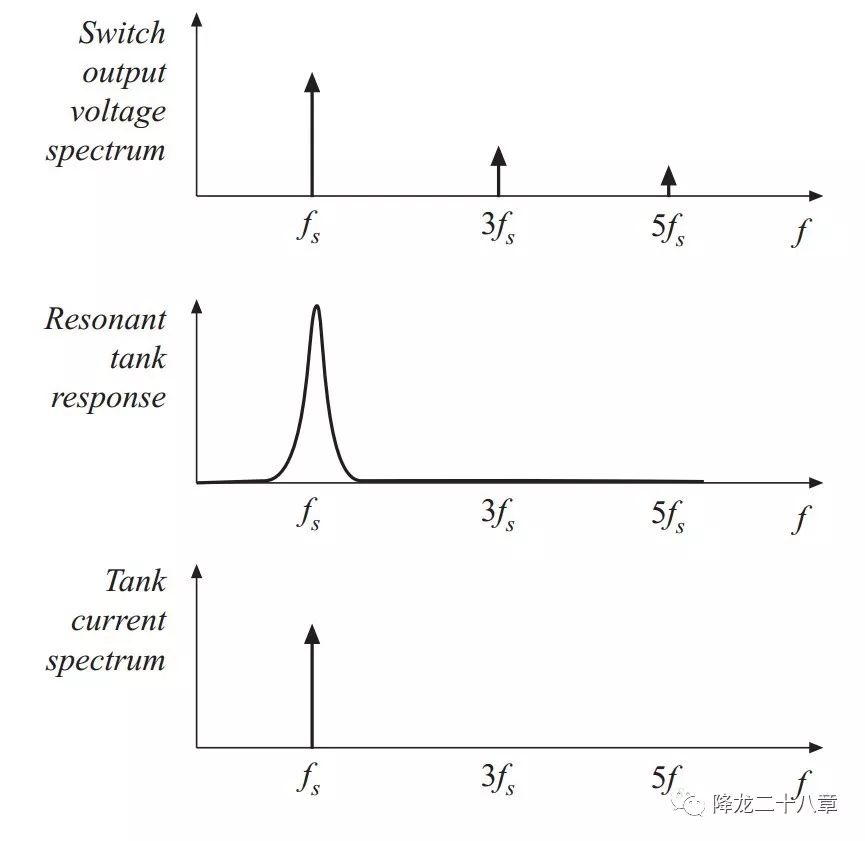
开关网络的输出方波电压做傅里叶分解后的基波电压如下

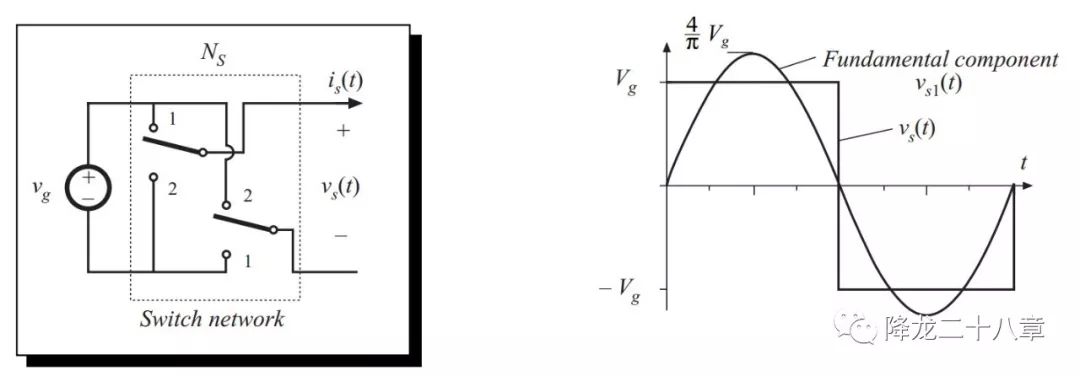
开关网络的输入电流波形如下

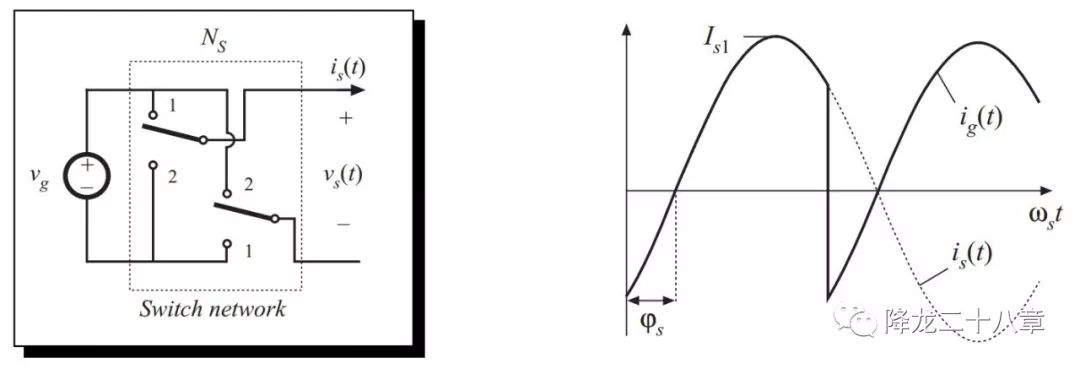
其中，ψs为谐振腔的响应电流（同时也是开关网络的输出电流）滞后于开关网络输出电压基波的相角，Is1为响应电流的幅值。

可以对开关网络输入电流求取一个周期内的直流分量

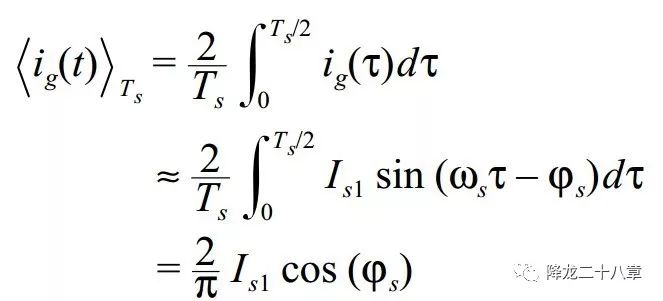
这样，我们可以把电源及开关网络等效成如下形式

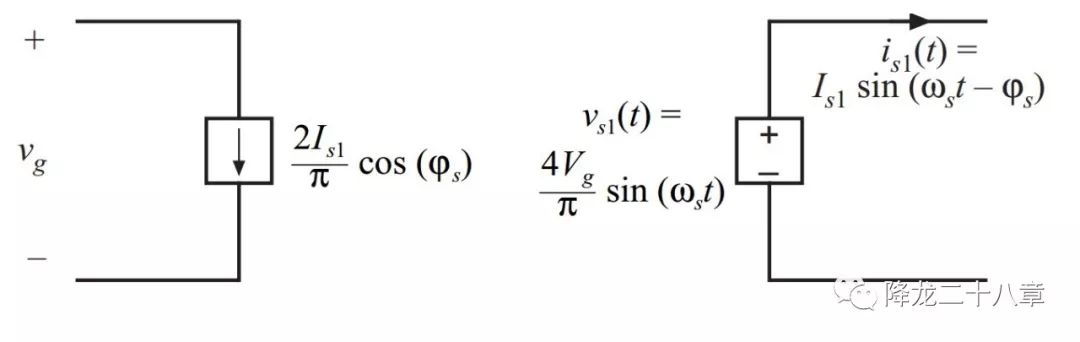
左边代表直流电源输出直流电，直流电负载即为开关网络输入电流的平均值。右边代表交流电压源给谐振网络输出交流电，交流电压源的幅值为开关网络输出方波电压的基波幅值，交流电频率为开关频率。

同样的方法，我们可以对整流网络和滤波网络等效，由于容性负载的存在，整流网络的输入电压为方波电压（V为输出直流电压）

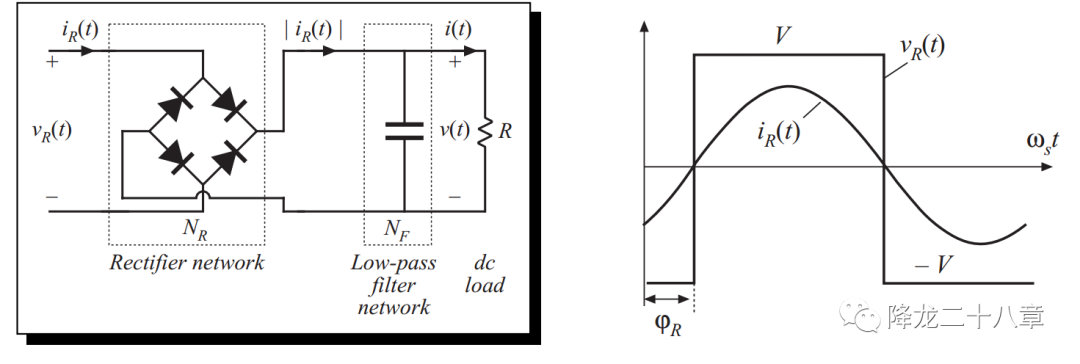
对整流网络的输出方波进行傅里叶分解，

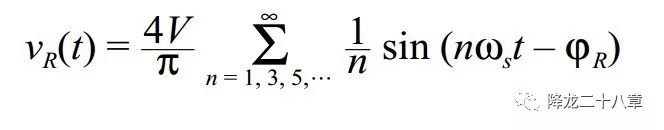
整流网络的输入电流为谐振网络的输出电流，（这里我们考虑的是LC串联谐振网络，谐振网络的输出电流与输入电流相等,is1=ir1,ψs=ψr,，如果是其他形式的谐振网络，则输入输出电流未必相等）：

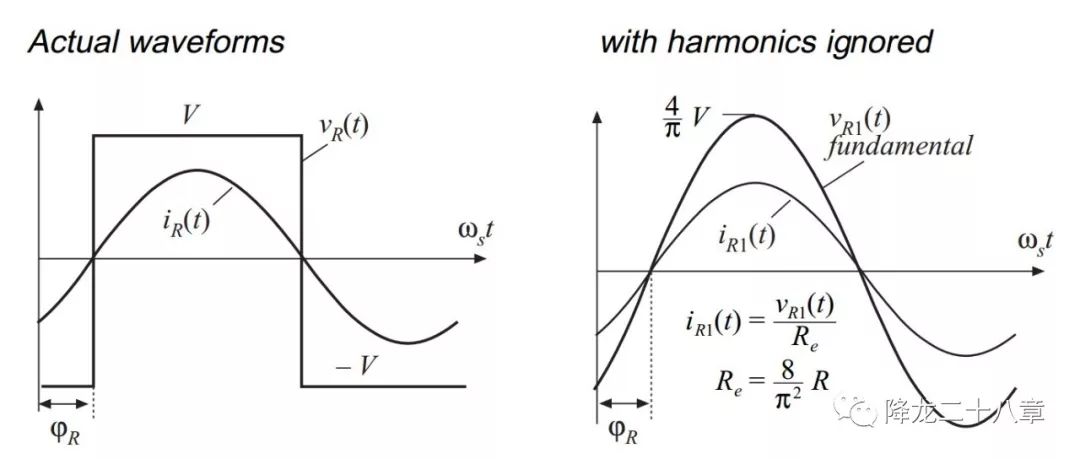
考虑整流网络的输入电压基波幅值与输入电流的幅值比例及相位关系，可以得到的整流网络及滤波网络（负载电阻为R）的等效输入阻抗，这个阻抗是一个纯电阻，可以表示为Re。

这样就可以得到由整流网络，滤波网络及负载电阻构成的等效电路如下图

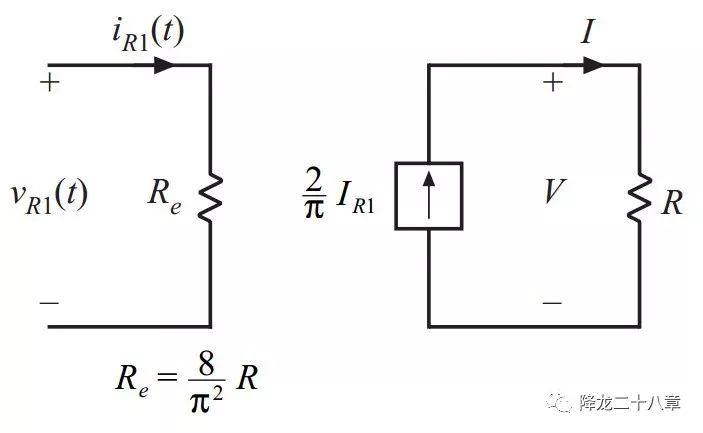
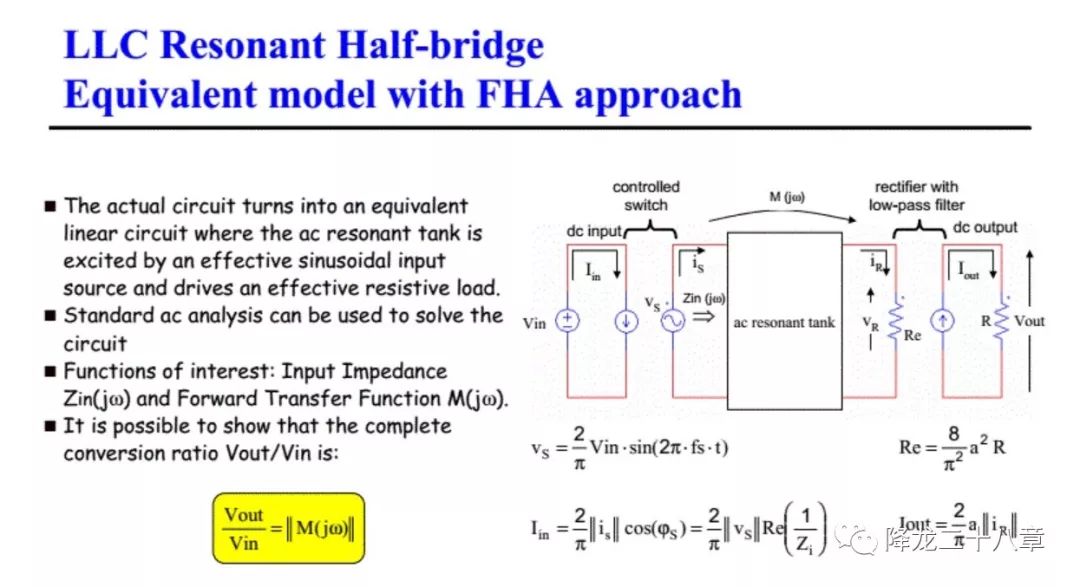
接下来，我们便可以对整个谐振变换器电路进行等效，非线性网络被等效成了线性网络。

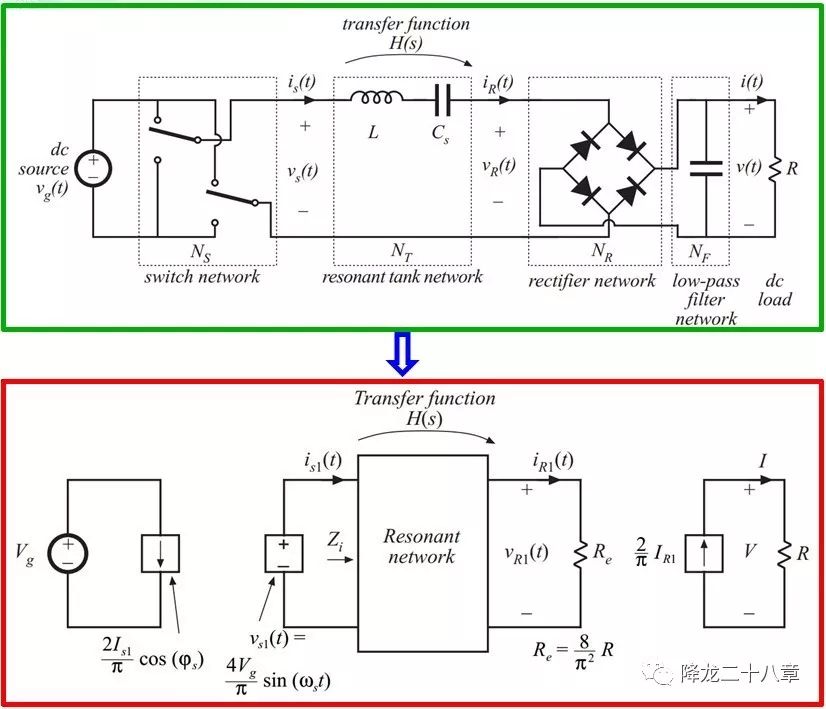
我们只需要关心等效后的谐振网络部分的频域特性，问题被大大简化。 这样的分析方法，被称为基波等效分析法 。这样，所有针对谐振变换器的分析工作，都可以围绕谐振网络的特性展开。

那么我们需要关心谐振网络的哪些特性呢？

1. 阻抗特性。分为输入阻抗和输出阻抗，输入阻抗的幅值决定了输入电流对输入电压的响应比例，这对于开关管的电流应力是决定性因素；输入阻抗的相角是实现开关管软开关的关键因素；对于输出阻抗，则决定了系统的阻抗匹配，当系统输出阻抗成纯阻性时，这时调节负载等效电阻Re，使其等于输出阻抗，Re变能获得最大的输出功率。
2. 增益特性。这个谐振变换器例子中的输出为电压源型负载，稳态的输出电压V与输入电压Vg的比例是这个电路的增益M，这个增益显然和谐振网络的输入输出电压传递函数H(s)有关。

以串联谐振变换器为例，输入输出电压增益M等于谐振网络输入输出电压传递函数H(s)的幅值（证明如下图），

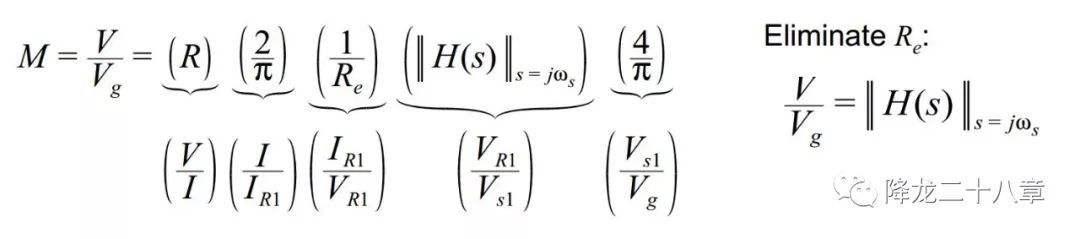
下图为串联谐振变换器的谐振网络输入输出电压传递函数。

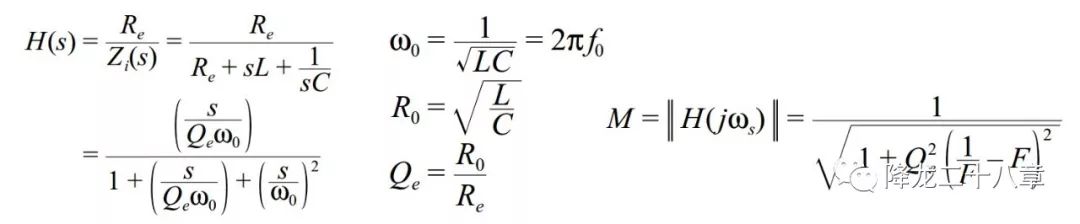
除了公式表示以外，还可以通过曲线图表示增益特性和阻抗特性

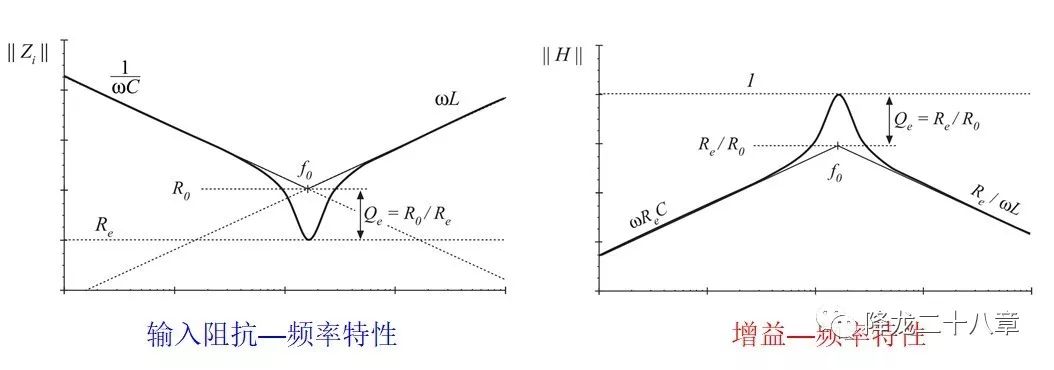
以上两点就是阻抗特性和增益特性分析谐振变换器的 两大利器 。可以看到，这两个特性都是和开关频率相关的，可以写成开关频率的函数，这就是典型的频域分析。

值得注意的是，传递函数这种频域函数只有在把自变量s换成了2πjf时才具有明确的物理意义。并且，传递函数是基于零初始状态的条件得到的，当系统的初始条件不可忽略时，传递函数的方法便不再适用，这时再采用时域微分方程结合电路模态分析是一种解法，但更多的时候，使用状态空间的方法会更简洁，有兴趣的读者可以参考现代控制理论的相关内容，这里不再赘述。

三.LLC电路实例

前文中，我们以串联谐振变换器为例，给出了谐振变换器的频域分析方法--基波等效分析法。这部分内容都是在从数学的角度建立模型，说白了就是空洞洞的理论。现在，我们便将这一理论应用到一个非常典型的实际变换器中，毕竟，实践是检验理论的唯一标准嘛。

提起LLC谐振变换器，相信大家都有所了解。业内有非常多的产品和研究工作就是基于LLC谐振变换器的，所以今天我们不再对它的电路模态这些细节做详细的介绍了。

我们把前文提到的两大利器应用到这个电路里面，让大家理解这个变换器最基本的道理就Ok。

如果看官们对LLC变换器的相关知识感兴趣，我给各位推荐两份资料，第一份是意法半导体（ST）制作的LLC分析文档，在百度文库上可以查到；第二份是一篇博士论文，题为Investigation of High-density Integrated Solution for AC/DC Conversion of a Distributed Power System。

首先，我们来看全桥LLC谐振DC/DC变换器的电路拓扑结构

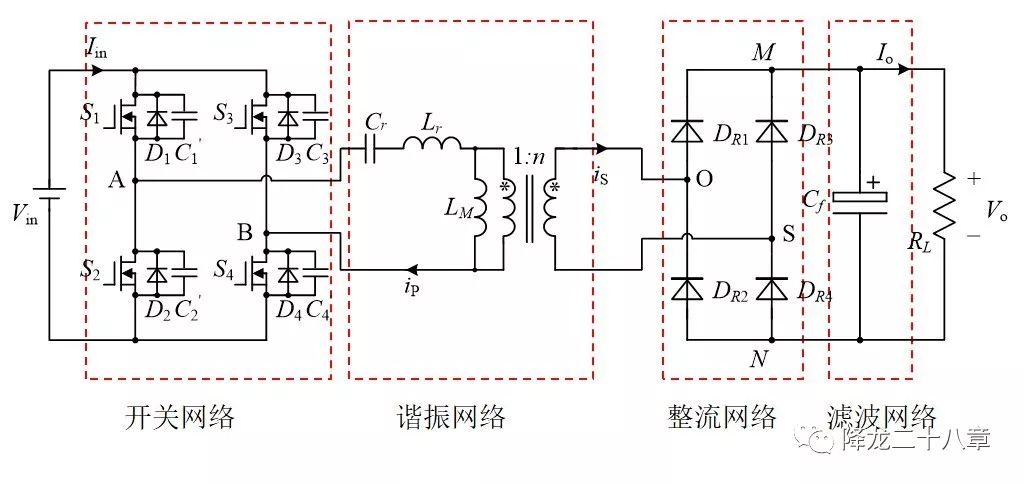
可以看到，这个变换器的结构与前文中的串联谐振变换器一样，可以分为开关网络，谐振网络，整流网络和滤波网络四个二端口网络。不同的是，这个电路拓扑的谐振网络是一个带变压器的二端口网络，并且有三个谐振元件，谐振电感，谐振电容，变压器励磁电感。

由于结构与上文分析的一致性，我们可以把上文中的分析方法应用到这个LLC拓扑中，同样关注谐振网络的频域特性。

和上一篇一样，我们再看看LLC谐振变换器的ZVS条件。

我们知道，谐振网络的输入电压基波与输入电流存在相位角，这个相位角就是输入阻抗在基波频率点的相位角。

那么这个相位角对于开关网络意味着什么呢？

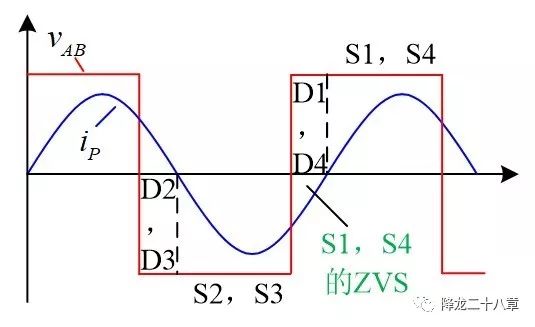
如下图，红色为方波输入电压，蓝色为原边的谐振电流，图中表现的是电流相位滞后于电压相位的情形。当VAB为负向输入电压时，表示2，3管导通，要么是2，3管的沟道导通电流，要么是2，3管的寄生二极管导通，可根据电流方向区分。当2,3管同时关断后，考虑死区时间，1，2，3，4管都是处于关断状态。如果此时的谐振电流为负值，便会给2，3管结电容充电，给1，4管结电容放电，如果能量足以将1，4管结电容电压降至零，再经1，4管的寄生二极管续流，便具备了实现软开关ZVS的条件。

接下来是电流超前于电压的情况。如下图，在VAB为负输入电压时，2，3管先由沟道导通负向电流，再由寄生二极管导通正向电流。电流从沟道换向二极管的过程，电流从峰值降到零，再变为负向，是一个自然换流的过程，此时即使S2,S3的驱动为高，电流也不再通过沟道流通。二极管续流一段时间后，S2，S3驱动变低，关断S2,S3，这就实现了S2,S3管的ZCS。关断S2,S3后，经过短暂的死区时间后再开通S1,S4。S1,S4开通时，二极管S2,S3还流通正向电流，但其电压迅速上升至输入电压，强制S2,S3关断，这时D2,D3会产生严重的二极管反向恢复问题，而此时S1,S4已开通，相当于桥臂形成直通，如果能量足够大，就有损坏器件的风险。另外，反向恢复过程还伴随较严重的电压震荡问题，不仅增加了损耗，而且可能超过器件的安全工作区导致失效。 所以ZCS的情况需要尽量避免。 这部分内容在我推荐的第一份资料里有详细的介绍，大家可以参考。

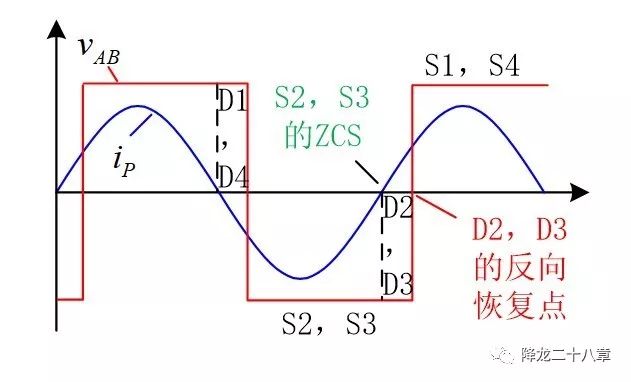
一般的LLC谐振变换器设计，会规定感性区和容性区，就是从输入阻抗的角度考虑的，因为感性区意味着电流相位滞后于电压相位，可以实现ZVS。而容性区则意味着电流相位超前于电压相位，是ZCS区，需要避免。

上文中我们讨论了输入阻抗特性对于开关网络ZVS的实现的作用，下面我们讨论增益特性对系统的影响。

下图是LLC变换器的归一化增益曲线，所谓归一化，就是将横坐标的开关频率fs换成了开关频率与谐振频率的比值fn。另外，我们把励磁电感Lm与谐振电感Lr的比例记为k，谐振网络特征阻抗与等效电阻Re的比值记为Q，可以得到增益函数是关于fn,k,Q的函数M（fn,k,Q)

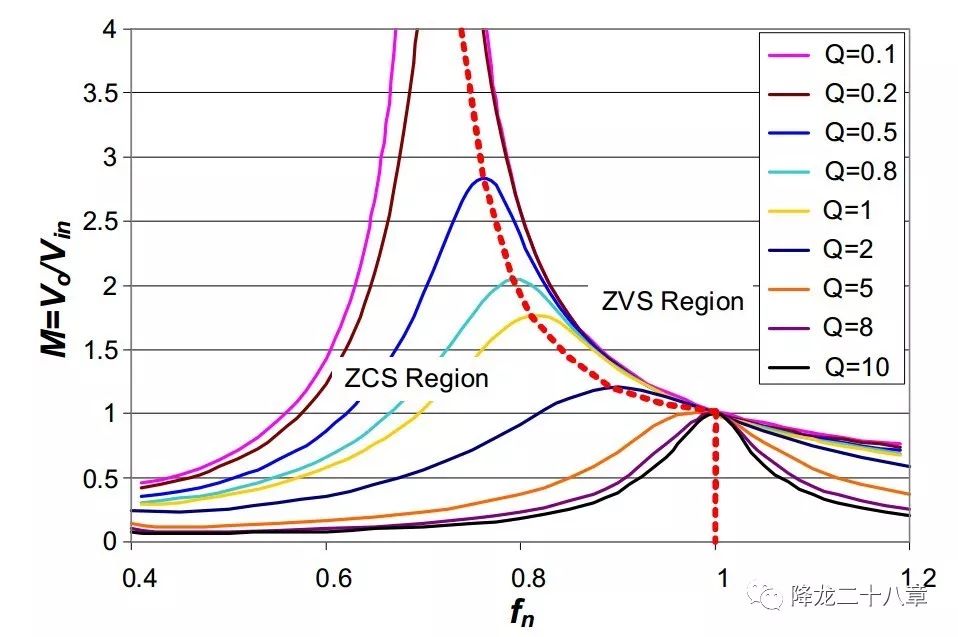
图中红色虚线为输入阻抗的纯阻性曲线，曲线的右边意味着感性区和ZVS，右边意味着容性区和ZCS。

值得注意的是，这个曲线是在某个特定的k下得到的，也就是说，改变励磁电感与谐振电感的比例，增益曲线的形状也会变化。

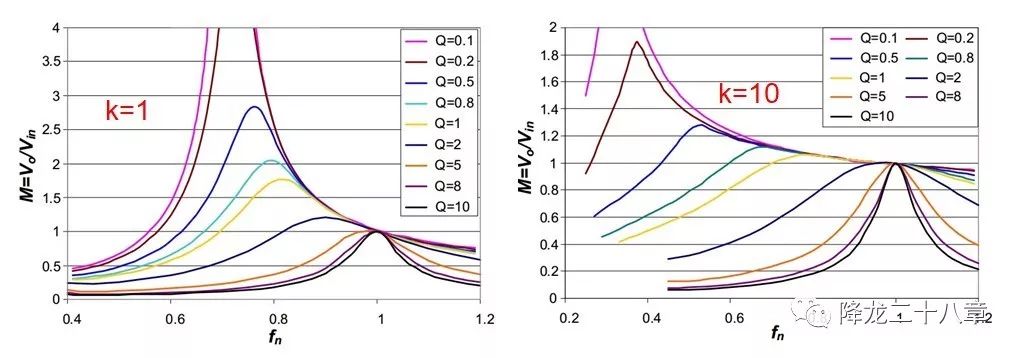
从图中可以看到，当k值变大后，增益曲线变“平坦”，这意味着要获得相同的增益变化范围，k值大的谐振网络需要的频率变化范围比k值小的谐振网络需要的频率变化范围更大。这即是我们所说到的敏感性，LLC谐振变换器的增益对开关频率的敏感性是和k值相关的。

在一些恒流输出场合，比如3.3kW的恒流输出的车载充电器，经过PFC整流后的母线电压是380V-420V直流，要通过LLC谐振变换器转化成70V-120V/30A的直流电压电流给电池供电，再比如中大功率恒流型LED驱动电源，同样PFC后的直流母线电压需要转化成20-48V的直流电压。这些场合输出电压变化范围宽，需要的电路增益变化范围较大，而控制器的开关频率变化范围是有限的。这时可以使用k值较低的谐振网络，使得开关频率的变化范围在控制器的输出能力之内。

但如果k值过小，会有什么问题？

k值较小，意味着励磁电感相对于谐振电感较小，励磁电流相对于谐振电流不可忽略。变换器进入轻载时，励磁电流带来的磁芯损耗较大。另外，原边电流中激磁电流的成分多，同时也增加了高频线损。下图为励磁电感较小（k=2)的一个例子，红色为桥臂中点电压VAB，黄色为原边电流ip。

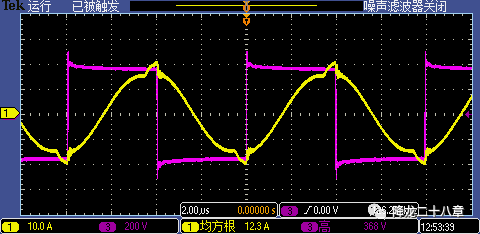
事实上，当我们规定了电路需要的最低增益，谐振频率和允许的最高开关频率后，我们可以定量地计算得到k值，具体参考ST的LLC文档。但在电路调试的过程中也会看到k值的影响，不止是在损耗和效率方面，k值对控制电路，电压应力等都是非常重要的。我们往往会对k值有一个预期，根据工程师经验，可以大概给出一个特定场合应用的k值范围。至于合不合理，就要看工程师的道行了。感兴趣的读者可以继续深入地分析k值对电路方方面面的影响。

对于LLC的具体设计，我提到的两篇文档中都有足够详细的内容，所以我不再多说。文档中提到的都是恒压输出的应用场合，感兴趣的读者可以思考恒流输出应用场合的设计有何异同。我们只提示大家一个方法，就是 寻找设计的边界条件 ，比如增益边界，最高开关频率，最大功率范围（空载到满载），ZVS实现条件。 如果弄清楚了各个边界与我们提到的Q值，k值等频域参数的关系，设计就迎刃而解了 。

总结

以上，我们把频域的分析方法应用到了串联谐振拓扑和常用的LLC拓扑中，重点关注了基波分析法的由来和阻抗特性，增益特性在变换器中的体现，希望大家看了之后看清谐振变换器的本质，不再被这些复杂的公式和流程吓倒。