控制上是怎么描述稳定性？如何判断一个系统是否稳定呢？

稳定的概念广泛存在于各个领域，大到飞机火箭桥梁建筑，小到生活中常见的各类电子产品生活用品，只要涉及到“可控”的要求，一定会谈到稳定性（Stability）。科学上，稳定性这种说法被归到了自动控制原理的范畴。

今天我们就带大家一起看看，控制上是怎么描述稳定性这件事情，希望能为大家的工作提供一些参考。

稳定性的概念涉及到很多理论知识，但太多的公式会把人绕晕，所以我们接下来多放图，只在必要的地方放入公式。如果大家很感兴趣，后面我们再从理论给出严格的推导。

首先，我们看下图，哪种颜色的球的状态当前是稳定的呢？

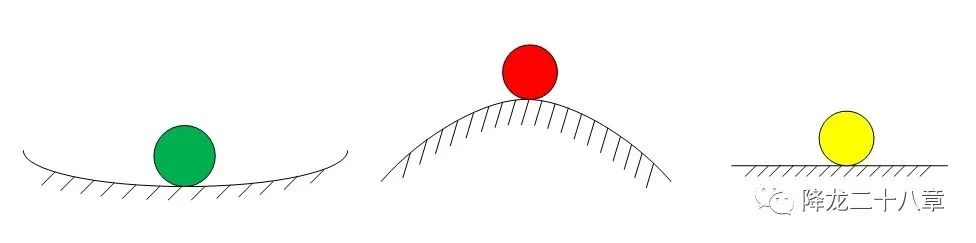
凭直觉，我相信大家都能猜到答案是绿球。

那么为什么认为绿球是稳定的呢，因为支撑它的地面是凹陷的。你给他一个小扰动，他最终还能回到原来的位置。不难发现，小球的稳定状态是由底面的结构决定的，与施加给小球的扰动无关。

稳定性是系统自身的性质，与系统的输入输出无关。

如何判断一个系统是否稳定呢？

时域到频域的映射，是通过拉普拉斯变换完成的。这样的拉式算子模型不仅可以存在于电路系统中，实际上，拉氏算子对任何经典线性控制领域的系统都是适用的。

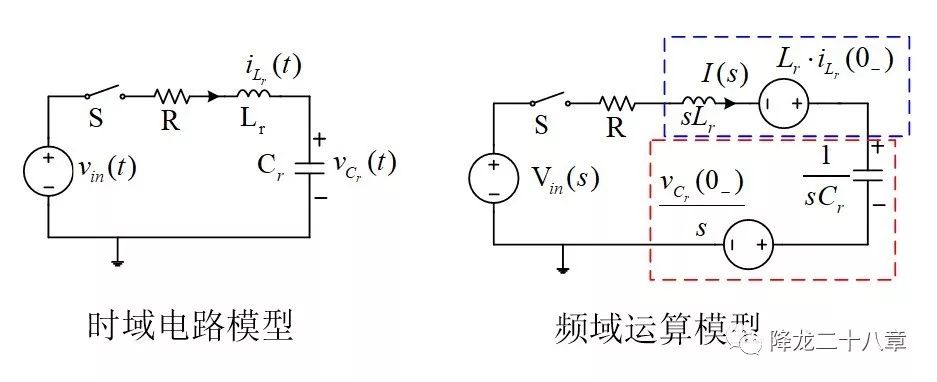
经典控制理论给出的方法是从系统的特征方程入手。这样的方法是基于：任何含有n个独立的一阶常系数微分方程的方程组，最后都可以将其转化成一个n阶微分方程 。特征方程就是这个方程。拉氏算子，只是一个微分符号。

例如，一个二阶LCR系统，其电容充放电关系和电感充放电关系构成的微分方程组就能构成一个二阶微分方程。

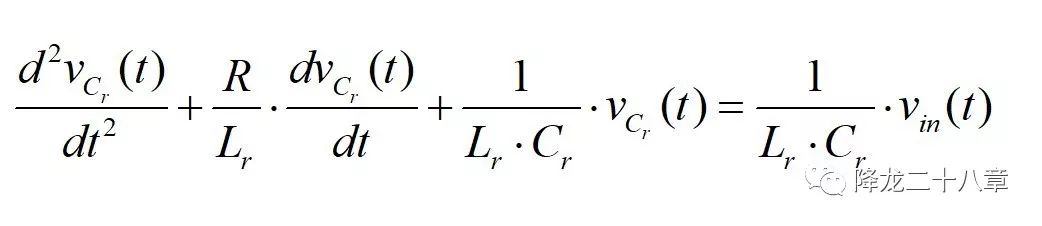
经典控制的所有理论，都是基于常系数线性微分方程的理论。但是单纯的微分方程，不具备任何物理意义。

因此控制理论中引入了极点的概念。

最简单的极点，就是一阶惯性环节的极点。在电路中，一阶惯性环节一般是由电阻和电容组成或者由电阻和电感组成。考虑下面这样一个电路：

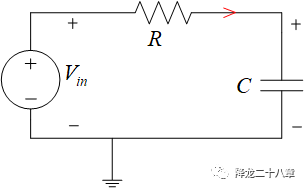
假设初始状态电压源输入为5V，且电路达到稳定，电容C的电压为5V，电阻电流为零。这时，我们给输入电压一个幅值为1V，脉宽为1ms的脉冲扰动。考虑上升沿的过程，由于电容电压不能突变，故电阻R两端形成5V的电压差，产生了电流，流进电容C（给电容充电）。

由于电容C的电荷量增加后其两端电压也增加，这样左边的电压源电压与右边的电容电压越来越小，充电电流越来越小，不久后就会形成一个新的稳态，即输入和电容电压均为6V，电流为零。下降沿亦是同理，电压最终回到5V。

我们对这种简单的一阶RC环节的系统方程可以说非常熟悉了，完全可以根据RC参数直接写出电容电压的表达式。从系统的特征方程出发，我们可以看到，这个系统仅存在一个极点，并且这个极点是在复平面（s平面）的负实轴上的。这个极点和RC常数相关。但这里我们不关心解析的结果，只关心这个过程对应的物理概念。

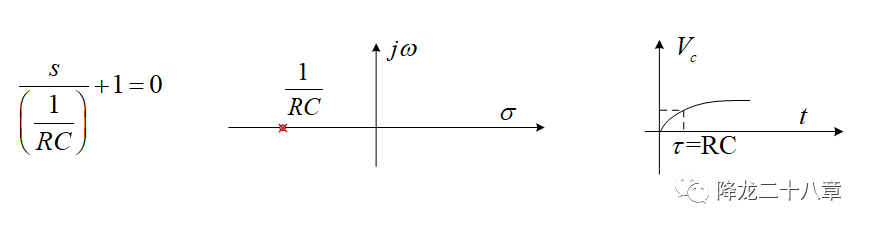
现在的问题是，这个RC系统中输出能够跟踪输入的最重要条件是什么？

--是电容的充放电特性。

怎样理解？因为给电容通正电流时，电容两端电荷积累，其电压升高，反过来再减小了电阻上的压差，从而减小电流，这本质上是一种负反馈。

倘若上图右边的元件不是电容元件，而是一种通入电荷，电压变低的特殊元件，那么这个负反馈就成了正反馈，不再具有收敛特性。

所以，一阶RC系统的负半平面的单极点至少具备这两个物理意义：

1）具有收敛特性，对应的是能量的损耗。

2）极点离虚轴越远，延时效果越差，离虚轴越近，延时效果越好。

经典控制系统一般考虑单输入单输出情况，因此可以认为一个复杂系统由多个子系统级联而成，系统的传递函数的分母都可以化成单个极点的乘积。因此，经典控制给出结论：系统稳定的充要条件是所有极点都在s平面的负半平面。

线性系统如果产生了正半平面极点，必定是不稳定和发散的。前文中的特殊元件是一个例子，还有其他一些反馈机制，也能形成不稳定和发散，这里不再举例。

"所有极点位于负半s平面"这样的稳定性判据虽然直观，但是涉及的计算量却是极大的，特别是当系统阶数比较高的时候，求取极点谈何容易！