

SaberRD的稳态分析验证概述
电子说
1.4w人已加入
描述
SaberRD—Stability Analysis
仿真可以大大减少通过测量进行稳态分析的工作量,但由于大多数电路模拟器缺乏在实际电路上进行交流分析的能力,实验室方法仍然流行。
SaberRD中的稳定性分析,对于了解系统在不同运行条件下的响应是非常重要的。与实验室测量相比,模拟能够更早地进行稳定性分析(减少时间和成本,仿真方法的灵活性)。一个系统可以是非线性的也可以是线性的,根据系统类型的不同,有周期交流分析、交流分析和零极分析等是在SaberRD中可以使用波德图(Bode plot)和极点-零图(Pole-Zero plot)验证系统的稳定性。
01
SMPS设计
频率分析
- 所面临的挑战
- 交流分析产生的频率响应电路线性化在一个偏置点。对于像滤波器和放大器这样的线性电路非常适用。
- 但是现在的设计包含了开关和数字设备,它们不是在一个偏置点上操作的,AC分析结果不是很有帮助。
- 解决方案
- 平均模型 → 交流分析
- 周期交流分析(Periodic AC Analysis)
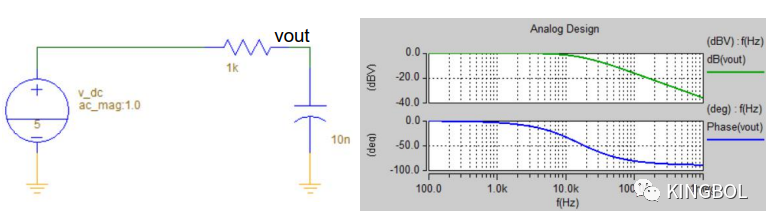

(线性)交流分析
- 频率响应是通过在单个偏置点附近线性化电路来确定的
- 该系统在频域进行解析求解
- 快速执行
- 同时计算所有信号
- 缺点:仅限于线性和平均模型设计
- 仿真分析
- 开关电源具有周期性的工作点,但无偏置点。
- 由于系统方程在工作点附近的线性化,交流分析不能计算切换系统的频率响应。



平均模型
- 非常有价值的长时域模拟,不关注小时间常数和高频影响(如电源管理分析)
- 使用时间连续方程
- 没有开关和数字电路
- 重要的建模工作

- 仿真分析:应用平均建模技术对时间连续方程转换模型进行描述



周期性交流分析(PAC分析)
- 通过对电路在小幅度正弦扰动下的时域仿真,得到了电路的频率响应
- 利用时域结果的傅里叶积分提取感兴趣信号的振幅和相位
- 也适用于非线性周期设计
- 不需要平均模型
- 缺点:限制选择的输出信号
- 仿真分析
- 保持原来的开关模式设计
- 选择小幅度扰动信号ac_mag(线性分析理论)
- 运行周期性交流分析;利用时域结果,通过傅里叶分析计算频率响应


02
PAC仿真分析
PAC分析
PAC分析内部算法
- 时域分析达到稳态
- 在稳态下注入扰动干扰
- 傅里叶计算
- 生成直方图
- 得到计算的波德图

PAC分析仿真设置
设置界面
- 输入源:选择用于交流扰动的通用源
- 输出信号:选择感兴趣的输出信号
- 开始频率:指定分析的开始频率
- 结束频率:指定分析的结束频率

- 输入源:PAC源连接在注入扰动的节点上
- 输出信号:需要频率响应的信号
- 开始和结束:频率需要响应的频率
- 点数:分析中使用的频率点的数目
- 延迟:直到系统达到稳态的时间或将-trip赋值为0

多频扰动:
- 仅从一次瞬态分析得到的频率响应,它叠加了所有扰动频率应用
- 适用至开关频率(奈奎斯特频率)的一半
- 无差错控制
- 比单频扰动快
- 参数含义:
- Ramp:多正弦扰动包络线从0上升到其最终值的时间间隔(秒)
- Settle:在多正弦斜坡结束和傅里叶分析开始之间的时间推移(秒)。这种时间的流逝允许在注入扰动后达到稳态。
- Acquire:执行FFT的周期1/fbegin的整数。大于默认值可用于过滤噪声
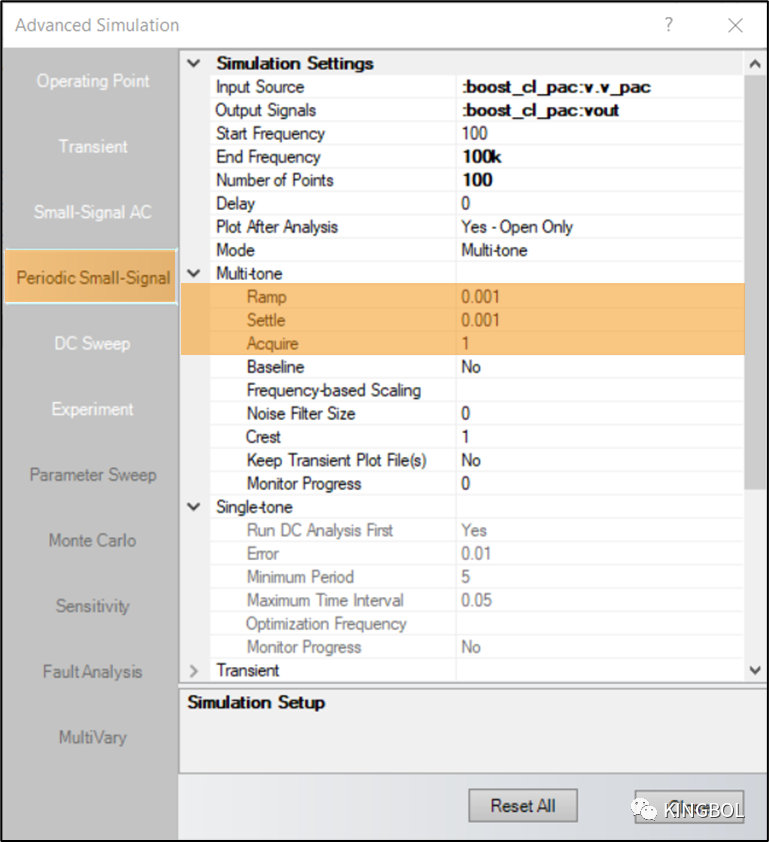
- Baseline:指定是否在没有多音扰动的情况下执行额外的瞬态分析
- Frequency-based:应用于单个正弦扰动作为频率的函数(例如,-freqscale freq1 scale1 freq2 scale2…)
- 噪声滤波器尺寸:用于减少波德图抖动的窗口平均滤波器的阶数。平均窗口的宽度是过滤器值的两倍
- Crest:对多正弦谐波分量的相位进行实数随机化,以减小波峰因子对大信号稳态的影响


单频扰动
- 从许多瞬态分析得到的频率响应
- 工作频率高于奈奎斯特频率(开关频率的一半和倍数除外)
- 误差控制
- 并行化可以提高性能多核网格/云计算
- 高效使用运行时附加组件产品
- 错误:傅立叶级数系数的收敛精度(减小-pac误差提高精度)
- 最低周期:每个频率点运行的最小周期数
- 最大时间间隔:傅立叶级数系数收敛的最大时间间隔
- 优化频率源幅值:为最佳信噪比而优化的频率

注意事项:
- 周期交流分析依赖于瞬态分析;建议“周期交流分析”中的TR设置与“瞬态分析”中的相同
- 周期性AC分析只能识别通用源
- 只支持一个交流电源.
- 频率增量限制为日志步长
- 过滤减少了博德图上的点的数量
- 扰动只应在设计处于稳态时启动
- 扰动的振幅是一种权衡,大到足以高于模拟噪声下限,小到足以避免扰动稳态操作(饱和效应)
03
PAC实现稳态分析
SPMS设计
稳定性分析开关模式电源设计一个闭环电源的工作流程设计:
- 1.在闭环路径中增加扰动源
- 2.运行定期AC分析
- 3.计算总体开环传递函数
- 4.应用稳定性测量
稳定性测量准则
- 增益交叉频率:
- 频率在增益=0dB时下降
- 应该小于开关频率的一半
- 相位差
- 相位差在增益=0dB和-180°之间
- 最好在45°-60°之间
DC-DC升压逆变器实例
设计设置

- 3型补偿器用于电压控制
- 多正弦扰动源连接在节点vout和vfb之间
- 摄动幅度:1mv
- 整体开环传递函数:
TF=Vout/Vfb
仿真设置

- 扰动来源:输入源:v.v_pac
- 感兴趣的信号输出信号:vout和vfb
- 启动频率:100hz
- 结束频率:99.9 kHz (100 kHz)
- 指定频率范围:100点
- 稳态时间延迟:40毫秒
- 校准的瞬态分析设置:时间步长:1n;截断误差:0.0005
仿真结果

应用稳定性分析

- 增益交叉频率:5233.3(小于开关电源频率的一半)
- 相位差:51.259°(不超过180°)
04
总结
Saber稳态分析的优势
- Saber提供PAC分析:一个强大的解决方案,以测试开关电源设计的系统稳定性
- 减少实验室的构建和测试
- 尽早发现问题灵活性,更容易假设降低成本缩短设计周期,减少平均建模工作量
- 降低成本
- 加快完成时间
- 提高品质
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
SaberRD外部模型导入功能—IBIS TOOL2023-12-06 2831
-
微分型单稳态触发器的Multisim分析2012-08-06 6909
-
正弦稳态分析2008-12-04 1098
-
非稳态导热的分析解视频教程2009-07-05 536
-
均匀传输线正弦稳态分析2009-07-27 1735
-
第7章正弦激励下电路的稳态分析2017-03-01 840
-
阻抗和导纳及正弦稳态电路的分析和功率的概述2018-07-25 2082
-
电动汽车背景及动力电池安全事故和电池验证性测试及数据分析概述2018-11-12 2372
-
控制系统的稳态特性稳态误差分析详细课件免费下载2018-11-22 1108
-
什么是稳态?浅谈PCBA设计中稳态热分析的目的2021-02-17 4217
-
什么是稳态?浅谈稳态热分析的目的2021-01-14 10562
-
FPGA中复位电路产生亚稳态概述与理论分析2020-10-25 3115
-
正弦稳态电路的分析学习课件免费下载2020-11-03 947
-
正弦交流电路的稳态分析2021-06-19 1581
-
亚稳态的分析与处理2023-06-21 5091
全部0条评论

快来发表一下你的评论吧 !

