计算中常见的RMS和RSS，你真的了解吗？

　　均方根值（RMS）和平方和的根值（RSS）是两个相关的概念，它们在数学上有相似之处，也有各自的适用范围，但绝不能混为一谈。

　　想象一个场景，我们在时间T1时刻对某个负载电阻施加电压E1。在此过程中会有一些功率耗散。该功率为P=E1²/R。然后，在T2时刻，我们施加E2，得到E2²/R，然后在时间T3时刻，我们施加E3，得到E3²/R，以此类推。

　　如果我们将时间标记保持紧密间隔，并且对从T1到Tn的时间执行同样的操作，我们将获得E1到En的平方和，即E1²+E2²+E3²+…+En²，这是传递到该电阻R的功率之和。获得该总和后，我们将该总和除以n以获得平均值，我们可以将其称为“平方和”的平均值。接下来，我们取“平方和”平均值的平方根，这样我们就找到了施加在R上的电压的RMS。

　　如果我们一直重复、重复、再重复施加电压的序列，那么RMS值就是稳定地施加到R上的电压，其功率输出和热效应与我们一直在讨论的电压施加序列相同。适用的计算公式也是我们非常熟悉的：

　　

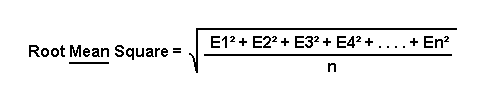
　　“平方和的根”也就是RSS，与RMS看起来很相似，但概念截然不同。RSS的计算公式如下：

　　

　　这两个概念之间的区别在于我们是否将总和或平方和除以“n”。 RSS与功率水平无关，但在微波系统分析中确实有应用。

　　所有微波系统都是由一些级联设备组成的，在每个设备间的接口处，都会存在一定驻波比（SWR）。如果每个设备的功率都是无损的，那么级联中的SWR就会产生一个复合系统的总驻波比，这个驻波比名义上是这些单个SWR的乘积。

　　很不幸的是，当我们试图估算出最坏情况下总驻波比的计算结果时，如果将其作为单个SWR的乘积，所得出的数字可能会高得离谱。在这种情况下，有时会决定将总驻波比的最坏情况估计为各个SWR的RSS。

　　请看图1中的图示：

　　

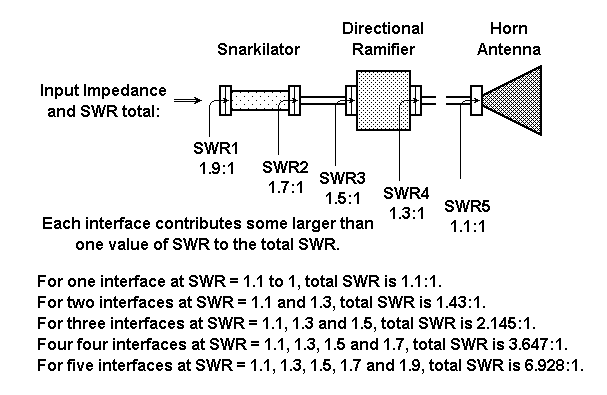
　　图1 设置总驻波比是设备间SWR的乘积。资料来源：John Dunn

　　只是编造一些可笑的设备名称，显示了1到5个设备间接口的计算，然后将这些值与图2中的RSS进行比较。

　　

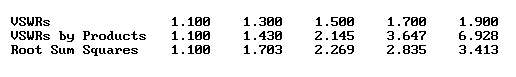
　　图2 1到5个设备间接口的乘积与RSS的比较。资料来源：John Dunn

　　总驻波比的RSS并不总是小于SWR乘积的计算结果，但有时会小于。对于图示的设备间SWR，RSS结果对于具有四个和五个接口的情况较小。

　　SWR为6.928:1的可能性非常小，因此在现实世界中，这样的结果可能会被视为不切实际。相比之下，3.413:1的SWR很可能是现实世界中最坏情况下SWR值的真实测量值。

　　我的客户不仅接受了这种解释，而且实际上也一直坚持这样计算。