

网联自动驾驶车辆通过信号交叉口的速度轨迹优化方案
描述
文章摘要
以网联自动驾驶汽车(Connected Autonomous Vehicle,CAV)为研究对象,研究了CAV车队通过城市信号交叉口的速度轨迹优化控制策略。基于最优控制理论,采用CAV的自动驾驶模型描述车间相互作用,以所有CAV车辆在行驶过程中的总油耗为优化目标,根据信号灯的配时信息建立模型约束,通过优化CAV头车的速度轨迹,保证整个CAV车队在绿灯相位下快速通过交叉口并实现油耗最小。
为了对该优化控制进行高效求解,采用离散Pontryagin极小值原理建立最优解的必要条件,利用基于神经网络训练的弹性反向传播(Resilient backpropagation,RPROP)算法设计了数值求解算法。多个典型场景的仿真结果显示:整个CAV车队均能在不停车的情形下通过信号交叉口,避免因在红灯时间窗到达停车线造成的停车、启动等过程,总油耗量最高可减少69.74%。该控制方法利用网联自动驾驶技术的优势,显著改善了城市交通通行效率和燃油经济性。
所提方法
1.CAV速度轨迹优化模型
本文采用C.Letter提出的自动跟车算法描述CAV的驾驶行为,见下式。
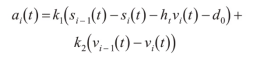
式中: i =1,2,…, n ;a**i ( t )为第i辆车t时刻的瞬时加速度,m/s ^2^ ;s**i ( t )为第i辆车t时刻的瞬时位移,m;v**i ( t )为第i辆车的瞬时速度,m/s;h**t为期望车头时距,s;d0为最小安全车间距,m;k1和k2为模型参数。
以CAV车队每1辆车的位移和速度作为状态变量(维数为2 n ), x =[s1v1s2v2 … snv**n ] ^T^ ,以CAV头车的加速度 u ,m/s ^2^ ,为优化控制变量,可以建立CAV车队行驶的状态方程模型 x ˙( t )= *f * [ *x* ( *t* ), *u* , *t* ],见下式。
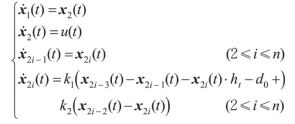
为了计算车辆在行驶过程的油耗量,需要建立油耗模型。车辆油耗模型有很多,考虑到该模型计算量会随着CAV车队车辆数增加而增加,为了提高计算效率,笔者采用欧洲环保局(European Environment Agency,EEA)开发的基于平均速率的COPERT油耗模型,见下式。
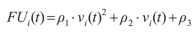
式中:ρ1 ,ρ2 ,ρ3为COPERT模型参数。
以所有CAV车辆的总油耗为优化控制的目标函数,见下式。
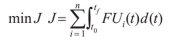
式中:t0和tf分别为控制初始时刻和终端时刻,s。
利用V2I通信,CAV获取交叉口的信号配时,假设距离当前时刻最近的绿灯相位时段[tg1 ,tg2 ],建立系统约束见下式。
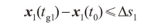
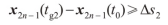
上式通过对CAV车队头车在tg1时刻的位移以及尾车在tg2时刻的位移进行约束,保证了CAV车队的所有车辆均能在绿灯相位时段[tg1 ,tg2 ]通过交叉口。
考虑汽车的能力限制,行驶的速度需要满足约束,见下式。
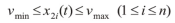
式中:vmin为最低车速,m/s,vmax为最高车速,m/s。
综上,式(2)和式(4)~(7)为基于最优控制的CAV速度轨迹优化模型,通过优化CAV头车的速度轨迹,便可以保证CAV车队所有车辆均能在绿灯相位下高效地通过交叉口,同时最小化所有车辆的燃油消耗总量,提高燃油经济性。
2 基于RPROP的求解方法
2.1最优解的必要性条件
为了在计算机上实现对上述最优控制问题的高效求解,对其进行离散化处理,接着通过惩罚函数法将不等式约束进行处理,通过引入拉格朗日乘子,将其转化为无约束的最优控制问题,最后利用离散系统Pontryagin极小值原理建立最优解的必要条件。
以Δt为离散步长,以[0,tg2 ]为优化控制周期,共K个离散时刻,kg1对应绿灯时间窗的开始时刻tg1 ,绿灯时间窗的结束时刻tg2为控制结束时刻 K 。采用差分法对CAV车队动态模型进行离散化,得到如下形式。
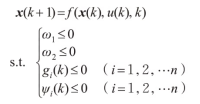
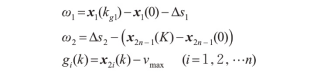
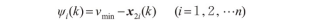
根据模型约束,构造如下惩罚函数:
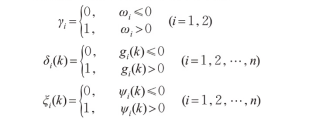
引入惩罚因子构造离散最优控制的增广目标函数:
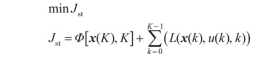
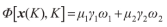
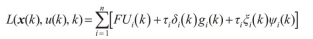
式中:为惩罚因子。
构造Hamiltonian函数,见下式。
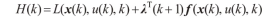
利用Pontryagin极小值原理建立最优解的必要条件。
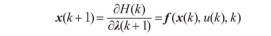
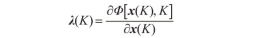
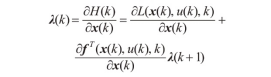
2.2基于RPROP的求解算法
采用基于神经网络训练的弹性反向传播算法(RPROP)方法,构造梯度方向,设计求解算法。其基本思想为:从某个初始值开始,根据Pontryagin极小值原理(见2.1节)得到梯度方向,并根据历史梯度信息动态更新搜索步长以加快求解速度,设计基于RPROP的求解算法。
离散化系统极小值的条件:
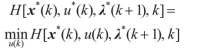
在搜索解的过程中,RPROP方法根据梯度符号决定搜索的方向,并根据搜索过程的结果动态调整搜索步长,可以保证求解的快速性。虽然RPROP方法无法保证收敛到全局最小值,但在实际应用中往往能获得比较满意的最优解。
梯度值 h ( k )可根据Hamiltonian函数见下式。
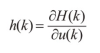
建立控制向量的迭代公式,见式(17)。
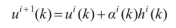
仿真实验
通过仿真实验,验证本文所设计的CAV速度轨迹优化策略。为了便于对比分析,分别将优化控制前、后的结果进行对比分析。在仿真过程中,假设交叉口停车线上游550 m处,有5辆车形成的CAV车队,初始速度为10 m/s,初始加速度0 m/s ^2^ ,V2I的最大通信距离为350 m(A点),也就是说:一旦CAV进入ICU可通信范围,即可与路侧基础设施进行通信。
初始时刻信号灯为绿灯相位,绿灯时间窗为[0,30 s],仿真结果见图1。
由图1可见,在该场景中,车队初始时刻以10 m/s的速度行驶。在没有采取优化控制的情况下,CAV车辆继续匀速行驶,错过了第1个绿灯相位(时间窗为[0 s,30 s]),在红灯相位时间到达停车线,唯有停车等待下1个绿灯相位。采取本文设计的速度轨迹控制策略后,CAV一旦进入ICU的通信距离,就可接收到ICU广播的信号配时信息,开始进行轨迹优化。CAV头车在优化过程中,不仅考虑本车,而且考虑整个车队的通行效率,于是CAV头车开始加速,使车队所有CAV车辆无需停车等待,均能在第1个绿灯相位通过交叉口。
由于优化过程中考虑了燃油经济性的优化,故加速过程中并未出现较大幅度的变速(整个运动过程中,0 m/s ^2^ ≤ a ≤2.93 m/s ^2^ ),经过COPERT模型的计算,总油耗量减少了69.74%。可见,通过本文设计的轨迹优化控制策略,CAV头车及时地根据信号配时信息进行轨迹优化,保证车队所有车的行驶效率,避免了因在红灯时间窗到达停车线造成的减速、停车、加速行为,显著减少了燃油消耗量。
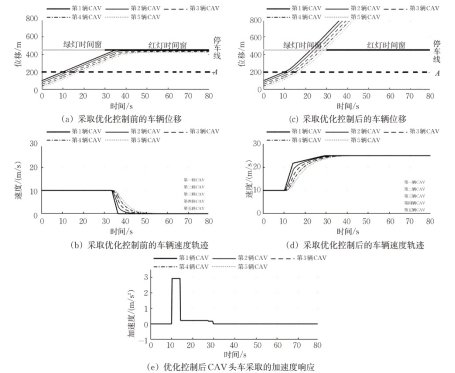
图1 场景1仿真结果对比图
阅读心得
本文构建了基于最优控制的CAV车辆通过信号交叉口的速度轨迹优化控制模型,并利用离散系统Pongryagin极小值原理建立最优解的必要条件,采用RPROP算法方法设计了求解方法,在保证求解质量的同时提高了求解速度。
仿真结果显示,CAV根据基于V2I通信获得实时信号配时信息,提前对自身速度轨迹进行调整,保证所有CAV车辆在绿灯相位时间窗无停车通过信号交叉口,避免因在红灯时间窗到达停车线造成的减速、停车、启动加速等过程,显著减少了所有车辆的总油耗,提高了通行效率。由于本文只考虑了CAV在单车道行驶的情况,在未来的研究中,将进一步研究CAV在多车道的行驶情况,考虑CAV的换道行为,对CAV的速度轨迹进行优化。
-
FPGA在自动驾驶领域有哪些应用?2024-07-29 8168
-
细说关于自动驾驶那些事儿2017-05-15 7013
-
自动驾驶的到来2017-06-08 7301
-
如何让自动驾驶更加安全?2019-05-13 3616
-
实现全自动驾驶尚需要众多技术革新之一智能网联汽车介绍2019-07-12 2800
-
从辅助驾驶到自动驾驶: 感知型车辆建立在底层高质量的传感器数据基础之上2020-06-16 2444
-
UWB定位可以用在自动驾驶吗2020-11-18 3605
-
网联化自动驾驶的含义及发展方向2021-01-12 4818
-
自动驾驶车辆中AI面临的挑战2021-02-22 2546
-
信号交叉口模糊逻辑自适应控制2009-07-30 464
-
RFID原理简介及其在交叉口车流量检测系统中的应用2017-10-30 1068
-
一种新型交叉口排队长度均衡控制方法2021-03-12 819
-
实现道路交叉口无信号灯控制2022-08-12 1866
-
业内首个穿越垂滑与服务车道交叉口的自动控制信号灯系统顺利交付2023-07-18 1694
-
交叉口的信号指示会对自动驾驶汽车产生什么影响?2025-08-24 1452
全部0条评论

快来发表一下你的评论吧 !

