深入浅出地讲解经典轴承故障数据集

冬至子 2023-12-06 6628

电子说

1.3w人已加入

描述

1 数据集解读

1.1 振动信号数据通常以时域显示

轴承

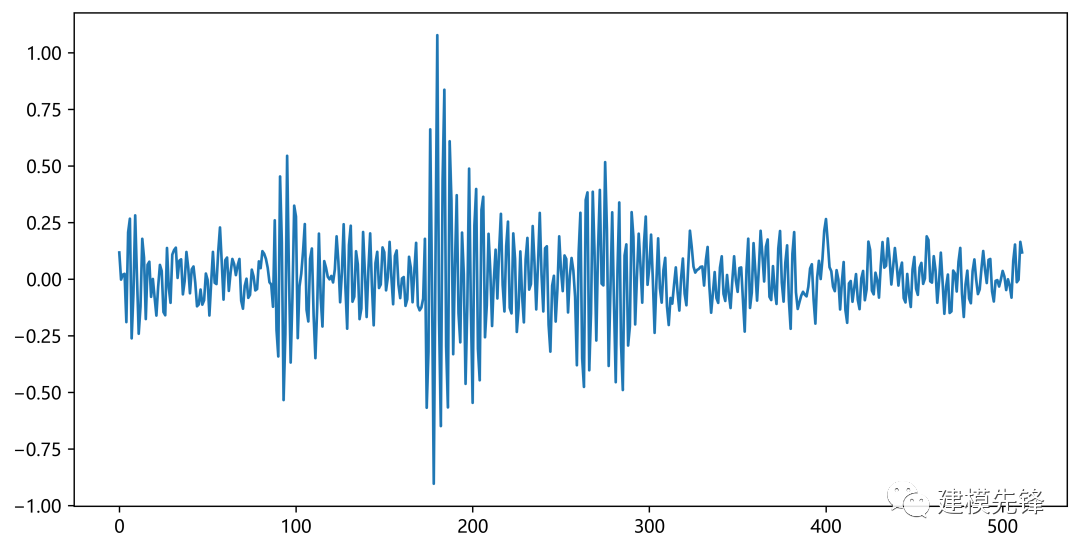
在轴承故障数据集振动信号的时域表示中，通常将时间作为横轴，振动信号的幅值作为纵轴。具体来说：

  • 横轴（X轴）代表时间： 时间是指振动信号采集的时刻或时间序列中的时间点。它表示了信号采集的顺序和时间间隔。横轴上的单位通常是秒（s）或毫秒（ms），取决于信号采集的频率和持续时间。
  • 纵轴（Y轴）代表振动信号的幅值： 振动信号的幅值表示了在特定时间点或时间段内的振动强度或振幅。它反映了振动信号的能量或振幅大小。在轴承故障数据集中，纵轴（Y轴）代表的是轴承的振动信号的幅值，以加速度（Acceleration）作为单位。纵轴上的数值表示轴承在特定时间点或时间段内的振动加速度值。

振动加速度是指物体在振动过程中的加速度变化，它是描述振动强度和振动频率的重要指标之一。在轴承故障数据集中，通过对轴承进行传感器测量，可以获取到轴承在运行过程中产生的振动信号，其幅值通过加速度来表示。

通过时域显示，我们可以观察到振动信号随时间的变化情况，包括振动的周期性、幅值的变化、脉冲或波形的形状等。这有助于分析信号中的特征、频率成分、周期性或随机性等，并对振动信号的特征进行故障诊断、频谱分析、波形分析等进一步处理和解释。

1.2 凯斯西储大学轴承数据集 描述的是什么数据？

该数据集是一个常用的轴承故障数据集，用于故障诊断和预测的研究。该数据集包含了来自不同故障模式和工作条件下的轴承振动数据。

数据集描述的是在旋转机械系统中使用的轴承的振动信号数据。轴承是旋转机械中的重要组件，常常承受着高速和高负荷的工作环境，因此容易发生故障。自身内部的缺陷有很多种像在加工生产时产生的或者在组装过程中导致的形变，外部环境所导致的故障也有很多种例如变形、磨损、裂变等。通过监测轴承的振动信号，可以获得关于轴承运行状态的信息，进而进行故障诊断和预测。

1.3 实验平台介绍

该实验台如图所示，其组成为：

  • 一个1.5KW（2马力）的电动机（图左侧）；
  • 一个扭矩传感器/ 译码器（图中间连接处）；
  • 一个功率测试计（图右侧）；
  • 电子控制器(图中没显示) 。

待测轴承：

  • 基座数据
  • 电机驱动端
  • 电机风扇端

1.4 以上三个不同位置的振动数据的区别解读

通过在电机壳体的 驱动端 、风扇端和基座上放置加速度计，可以获取到三个不同位置的振动数据。这些数据的区别在于它们所测量的振动信号反映的是不同的物理现象和特征，因而可以提供不同的信息用于故障诊断和监测。

  • 驱动端数据： 位于电机壳体的驱动端的加速度计测量的是电机驱动端的振动信号。这个位置上的振动信号主要受到电机转子的旋转和传动系统的激励影响，因此可以提供关于电机传动系统和驱动端的故障信息，例如轴承故障、齿轮啮合故障等。
  • 风扇端数据： 位于电机壳体的风扇端的加速度计测量的是电机风扇端的振动信号。这个位置上的振动信号主要受到风扇叶片的旋转和风扇系统的激励影响，因此可以提供关于风扇系统的故障信息，例如风扇叶片失衡、风扇轴承故障等。
  • 基座数据： 位于电机底座的加速度计测量的是整个电机系统的振动信号。这个位置上的振动信号受到电机整体结构和运行状态的影响，可以提供关于整个电机系统的故障信息，例如电机不平衡、底座松动等。

因此，通过收集不同位置上的振动数据，可以综合分析不同位置所提供的故障特征，从而更全面地了解电机系统的健康状况和故障状态。这有助于提高故障检测的准确性和针对性，以便及时采取适当的维护和修复措施。

1.4 官网数据集介绍

这是西储大学轴承数据中心网页下载数据的界面

轴承

  • DE - 驱动端加速度计数据
  • FE - 风扇端加速度计数据
  • BA - 基座加速度计数据
  • time - 时间序列数据
  • RPM - rpm during testing 转每分钟

第一个数据集：正常基线数据

轴承

Motor Load (HP) 的中文意思是电机负载（马力）。它表示施加在电动机上的功率或负载，通常以马力（HP）为单位进行衡量。它代表电机所执行的工作量或所生成的功率。在0、1、2和3马力的电机负载工况工作条件下记录振动加速度信号数据。

Motor Speed (rpm)：近似电机转速（rpm）

在不同负载和转速下一共有四组正常的数据，数据文件为Matlab格式。用Python读取第一个数据集结果如下：

data=loadmat('97_0.mat')
data

{'__header__': b'MATLAB 5.0 MAT-file, Platform: PCWIN, Created on: Mon Jan 31 15:28:20 2000', 
  '__version__': '1.0', 
  '__globals__': [], 
  'X097_DE_time': array([[ 0.05319692],        [ 0.08866154],        [ 0.09971815],        ...,        [-0.03463015],        [ 0.01668923],        [ 0.04693846]]), 
  'X097_FE_time': array([[0.14566727],        [0.09779636],        [0.05485636],        ...,        [0.14053091],        [0.09553636],        [0.09019455]]), 
  'X097RPM': array([[1796]], dtype=uint16)}

数据为字典格式，包括了创建版本信息、驱动端、风扇端、RPM转速信息等

**第二个数据集：**12k 驱动端轴承故障数据

采样频率为12 kHz，数据收集在12,000次/秒。

轴承

故障直径（Fault Diameter）：指轴承或其他机械部件上出现的故障或损伤的直径尺寸。故障直径通常用来描述故障的大小和程度，对于故障诊断和预测维护非常重要。单位为英寸，1英寸=25.4mm

  • 0.007英寸=7 mils =0.177 8 mm
  • 0.014英寸=14 mils =0.355 6 mm
  • 0.021英寸=21 mils =0.533 4 mm
  • 0.028英寸=28 mils =1.016 mm

Motor Load (HP)电机负载和Motor Speed (rpm)电机转速同上。

轴承

在轴承中，"Inner Race"（内圈）、"Ball"（滚珠）和"Outer Race"（外圈）是三个重要的组成部分，它们一起构成了轴承的基本结构。下面是它们的具体含

  • Inner Race（内圈）：内圈是轴承的一个环状部件，通常位于滚珠或滚子之内，与轴相配合。内圈通过与滚动体接触，在轴上旋转，承受和传递轴向和径向负荷。
  • Ball（滚珠）：滚珠是轴承中的滚动体，它们通常是小球状的物体，可以在内圈和外圈之间滚动。滚珠在轴承中起到支撑和传递负荷的作用，减少摩擦和滑动。
  • Outer Race（外圈）：外圈是轴承的另一个环状部件，位于滚珠或滚子的外部。外圈与内圈和滚珠配合，提供轴承的外部支撑和固定。

这三个部分共同工作，形成了轴承的基本结构，以支撑和传递轴上的负荷，减少摩擦，并使轴承能够平稳运转。它们的材料和设计会根据不同的应用和轴承类型而有所差异，以满足特定的负荷和工作环境要求。

驱动端和风扇端轴承外圈的损伤点分别放置在3点钟、6点钟、12点钟三个不同位置。所以外圈的损伤有三个数据集。

用Python读取第一个数据集IR007_0结果如下：

data = loadmat('105.mat')
data

{'__header__': b'MATLAB 5.0 MAT-file, Platform: PCWIN, Created on: Mon Jan 31 13:49:59 2000', 
'__version__': '1.0', 
'__globals__': [], 
'X105_DE_time': array([[-0.08300435],        [-0.19573433],        [ 0.23341928],        ...,        [-0.31642363],        [-0.06367457],        [ 0.26736822]]), 'X105_FE_time': array([[-0.40207455],        [-0.00472545],        [-0.10663091],        ...,        [ 0.31598909],        [ 0.35091636],        [ 0.03307818]]), 
'X105_BA_time': array([[ 0.06466148],        [-0.02309626],        [-0.08852226],        ...,        [ 0.09648926],        [ 0.08405591],        [-0.02015893]]), 
'X105RPM': array([[1797]], dtype=uint16)}

数据为字典格式，包括了创建版本信息、驱动端、风扇端、基座RPM转速信息等

查看一下驱动端数据条数

data1['X105_DE_time'].shape
(121265, 1)

将近12万条，也就是采集了近10秒的数据

第三个数据集：48k 驱动端轴承故障数据

驱动端轴承故障还包含采样频率为48 kHz 的数据，数据收集在

48,000次/秒。

轴承

其分析同上。区别是采样频率不同，故障直径（Fault Diameter）少一种。

第四个数据集：风****扇端轴承故障数据

风扇端采样频率为12 kHz 的数据，数据收集在12,000次/秒。

轴承

其分析同上。区别是对象和采样频率不同，故障直径（Fault Diameter）也少一种。

上述四种数据集下载后如下

轴承

2 数据集分类与制作

2.1 数据集分类解读

凯斯西储大学轴承数据集包含了以上四种不同故障模式的振动数据，包括内圈故障、外圈故障、滚动体故障。数据集提供了不同工作条件下的实验数据，包括不同转速、载荷和工作时间等参数。每个故障模式都有多个不同工况的样本，按照不同条件约束，其分类形式有多种。

当然，如果需要处理这些数据，来进行故障诊断和分类任务，并不是需要网站中的所有数据，可以只选择我们需要的，比如选择驱动端+0HP的故障数据。

以 12k Drive End Bearing Fault Data 举例说明：

轴承

首先，有四种故障类型 ，只取前三种，因为0.028没有外圈故障。

轴承

其次，比如0.007文件，只取前三类，因为第三种负载 和第四种负载差不多。

轴承

最后 ，外圈故障 只取Outer Race _6，即6点钟的数据集，因为每个文件都有，而且数据差别也不大。

综上：三种直径数据和三种故障数据，所以每个工况共有3*3+1（正常数据）=10种数据。所以根据工况的不同可以把数据分为A、B、C三种。每个工况有10种数据。如下：

  • 正常0hp 为一类
  • 0.007 0hp 内圈 滚珠 外圈
  • 0.014 0hp 内圈 滚珠 外圈
  • 0.021 0hp 内圈 滚珠 外圈

2.2 数据集处理与制作

第一步，数据读取：

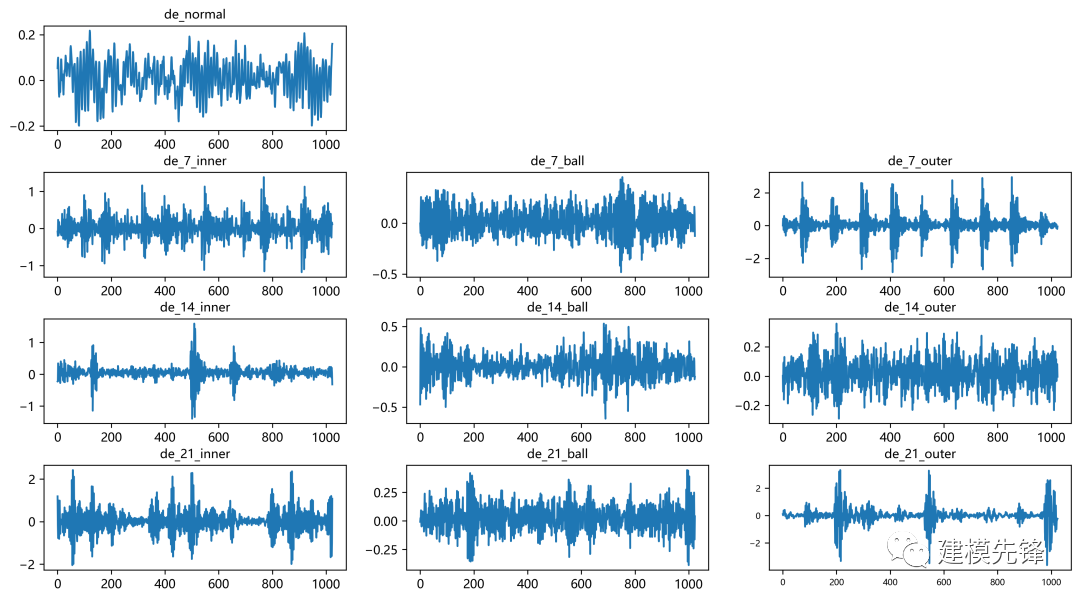
十类数据集，每类数据集中只获取DE_time数据，Python读取数据如下所示：

# 采用驱动端数据
data_columns = ['X097_DE_time', 'X105_DE_time', 'X118_DE_time', 'X130_DE_time', 'X169_DE_time',
                'X185_DE_time','X197_DE_time','X209_DE_time','X222_DE_time','X234_DE_time']
columns_name = ['de_normal','de_7_inner','de_7_ball','de_7_outer','de_14_inner','de_14_ball','de_14_outer','de_21_inner','de_21_ball','de_21_outer']
data_12k_1797_10c = pd.DataFrame()
for index in range(10):
    # 读取MAT文件
    data = loadmat(f'E:codeingVscodeProjectsDeepLearning故障诊断data_deal_1797{file_names[index]}')
    dataList = data[data_columns[index]].reshape(-1)
    data_12k_1797[columns_name[index]] = dataList[:119808]  # 121048  min: 121265
print(data_12k_1797_10c.shape)
data_12k_1797_10c

把数据生成后放在一张表格里（矩阵形式）10列不同分类故障数据标签，一共将近12万行数据，如下图所示

轴承

然后保存为CSV形式，以便后续处理。

data_12k_1797.set_index('de_normal',inplace=True)
data_12k_1797.to_csv('data_12k_1797_10c.csv')

对10分类数据时序图数据可视化，二维图像辨识度比较高。

轴承

第二步，制作数据集：

数据集的切分方式也多种多样，切分步长也具有多样性，下面按照固定的参数设置进行数据的切分：

  • 步长 window_step：512 （每个样本长度为512个点）
  • 重叠率 overlap_ratio：0.5（切分相邻两个样本重叠率）

怎么理解重叠率呢？举例如下：

轴承

切分样本点后，按照7：2：1划分训练集、验证集、测试集，最后保存数据：

轴承

3 基于Python的故障诊断和分类的研究思路

3.1 关于轴承故障类型分类的方法探讨

第一类是对一维故障数据进行分类

  • 一是直接对一维故障数据，添加分类标签进行处理，送进CNN、LSTM等网络进行分类；
  • 二是先对一维故障数据做一些处理或者去噪，然后再进行分类；

第二类是把一维故障数据转换为图像进行分类

  • 一是转换为二维时序图进行分类；
  • 二是转换为时频图像进行分类；
  • 三是基于格拉姆角场(GAF)转换为二维图像进行分类；

3.2 重点介绍关于轴承故障数据时频图像分类的方法

滚动轴承发生故障时，其振动信号往往具有非线性、非平稳性特点。相比传统的时域和频域分析方法，在处理非线性、非平稳信号时，时频分析方法更加有效。

时频分析方法采用时域和频域的二维联合表示，可以实现非平稳信号局部特性的精确描 述，具有时域和频域等传统方法无法比拟的优势，已经被广泛地应用于机械故障诊断领域。

常用的时频分析方法有：

  • 傅里叶变换（Fourier Transform，FT）
  • 短时傅里叶变换（Short Time Fourier Transform，STFT）
  • 小波变换（Wavelet Transform，WT）
  • 连续小波变换（CWT）

下面以连续小波变换（CWT）作为轴承故障数据的处理方法进行讲解：

第一步，Python中连续小波变换（CWT）介绍

导入相关包，pywt 用于小波变换

import numpy as np

import matplotlib.pyplot as plt

import pywt

import pandas as pd

加载轴承数据集 驱动端故障数据

data3 = loadmat(r'21_2.mat')
data_list3 = data3['X222_DE_time'].reshape(-1)
data = data_list3[0:512]

设置连续小波变换参数 设置采样周期为 1/12000，总尺度为 128，小波基函数选择 'cmor1-1'

sampling_period  =1.0/12000
totalscal = 128    
wavename = 'cmor1-1'

计算小波基函数的中心频率 fc

fc = pywt.central_frequency(wavename)

然后根据 totalscal 计算参数 cparam

cparam = 2 * fc * totalscal

通过除以 np.arange(totalscal, 0, -1) 来生成一系列尺度值，并存储在 scales 中

scales = cparam / np.arange(totalscal, 0, -1)

轴承

生成时频图

轴承

第二步，生成时频图像数据集

轴承

如图所示为生成的图像数据集

轴承

第三步， 定义数据加载器和VGG网络模型

制作数据标签，保存数据

轴承

定义VGG网络模型

轴承

第三步，设置参数，训练模型

30个epoch，准确率将近90%，继续调参可以进一步提高分类准确率

轴承

打开APP阅读更多精彩内容
声明：本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人，不代表电子发烧友网立场。文章及其配图仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。 举报投诉

全部0条评论

快来发表一下你的评论吧 !

下载APP
|投诉反馈|电子发烧友网
© 2021 elecfans.com
湘ICP备2023018690号
×
20
完善资料，
赚取积分