设计双边射频放大器以实现最大增益的方法

本文要点

设计双边射频放大器可以实现最大换能器增益，并需要考虑晶体管的反向增益。

单边品质因数（U）可以评估晶体管的反向增益是否可以忽略不计。

如果U小于0.1，则可以使用单边方法来设计放大器，误差小于约±1dB。

本文概述

本文介绍了设计双边射频放大器以实现最大增益的方法。在单边设计方法中，可以使用单边品质因数（U）来评估晶体管的反向增益是否可以忽略不计。如果U小于0.1，可以使用单边方法来近似实际增益。然而，当U较大时，需要采用双边设计方法来考虑晶体管的反向增益。在双边设计中，需要同时共轭匹配输入和输出端口以实现最大增益。最大增益的单边设计实际上是双边方法的一种特例，其中晶体管的反向增益被设置为零。公式和图表可用于计算和优化放大器的性能。 

本文探讨了双边射频放大器的设计，以实现最大换能器增益，并解释了如何评估射频放大器是双边放大器还是单边放大器。

不同的射频放大器有不同的性能要求。例如，实现最大输出功率可能是位于发射器输出处的功率放大器的主要关注点，但放置在射频接收器前端的低噪声放大器 (LNA) 的设计可能会侧重于提供可接受的功率水平。功率增益与尽可能最小的噪声。LNA 之后出现的其他放大级可能旨在实现最大增益。

在本系列的上一篇文章中，我们学习了如何设计具有指定增益的单边射频放大器。在本期中，我们将重点关注设计双边射频放大器以实现最大换能器增益。然而，首先，我们将学习如何确定设备是否是双边的。

单边品质因数

使用单边器件，可以独立设置输入和输出匹配部分的增益，这大大简化了设计方程。实际上，晶体管并不是完全单边的，但如果S 12足够小，我们仍然可以使用单边方法，而不会产生重大错误。

但什么才算是“足够小”的S 12呢？我们可以使用单边品质因数（U）来评估晶体管的反向增益是否可以忽略不计。单方面品质因数由下式给出：

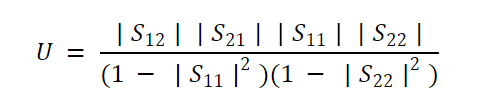
等式 1。

请注意，U是所有 S 参数的函数，而不仅仅是S 12。因此，U也与频率相关。

当我们忽略晶体管的反向增益并假设S 12 = 0 时，我们通过放大器的单边传感器增益 ( G TU ) 来近似放大器的实际传感器增益( GT )。通过显示这两个增益项的比率与U的关系，方程 2 使我们能够估计通过将S 12近似为零而获得的计算单向增益与电路表现出的实际增益之间的差异。

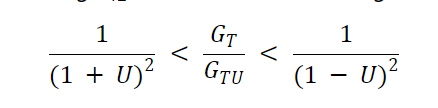
等式2。

由于与U的这种关系，当S 12 ≠ 0时，所有 S 参数都会对误差幅度产生影响。图 1 提供了以 dB 为单位的误差与单边品质因数的双对数图。

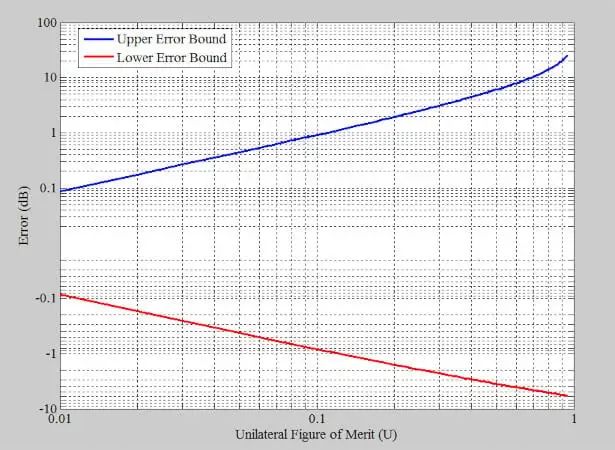
图 1.单边增益计算误差与单边品质因数。图片由 Steve Arar 提供

我们可以看到，随着U变大，误差迅速增加，因此对于较高的U值使用单边近似可能不是一个好主意。然而，如果U小于0.1，则单边方法的误差小于约±1dB。当晶体管为单向晶体管 ( S 12 = 0) 时，公式 1 产生U = 0，使传感器增益等于单向传感器增益（零误差）。

示例1：计算误差

图 2 绘制了具有小但非零S 12的晶体管的单边品质因数与频率的关系。如果我们将S 12近似为零，实际增益与设计的单边增益会相差多少？

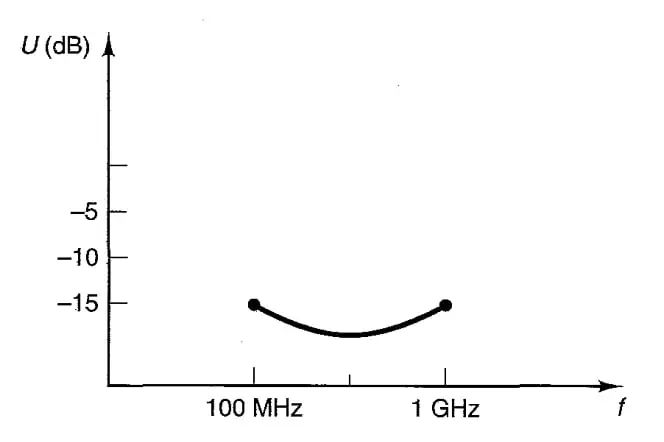
图 2.具有小型非零S 12 的晶体管的单边品质因数与频率的关系。图片由G. Gonzalez提供

上图显示U小于 –15 dB（或线性项 0.03）。使用公式 2，我们可以找到误差界限的精确值；或者，我们可以使用图 1 的方程图作为图形解。根据图1，本例中单边法的误差小于±0.3 dB。

值得一提的是，公式 2 只给出了最坏情况的误差。实际误差可能要小得多。即使在这种情况下，这个方程仍然非常有用——它可以帮助我们快速找到最大误差的极限。

双边设计法

当单边设计的误差过大时，就需要采用双边设计的方法，这样可以兼顾晶体管的反向增益。考虑图 3 中的基本单级放大器。

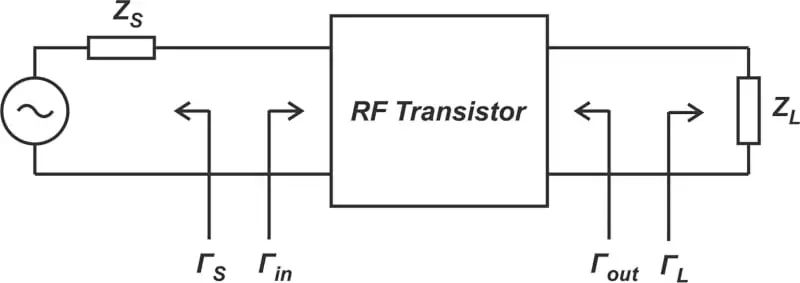
图 3.单级放大器。图片由 Steve Arar 提供

放大器具有其组件晶体管的 S 参数，因此其性能是其源端和负载端接（Г S和 Г L ）的函数。使用单边方法，我们只需设置 Γ S = S 11 * 和 Γ L = S 22 * 即可获得最大增益。当晶体管是双边的时，我们仍然需要在输入和输出端口提供同时共轭匹配以获得最大增益，以便：

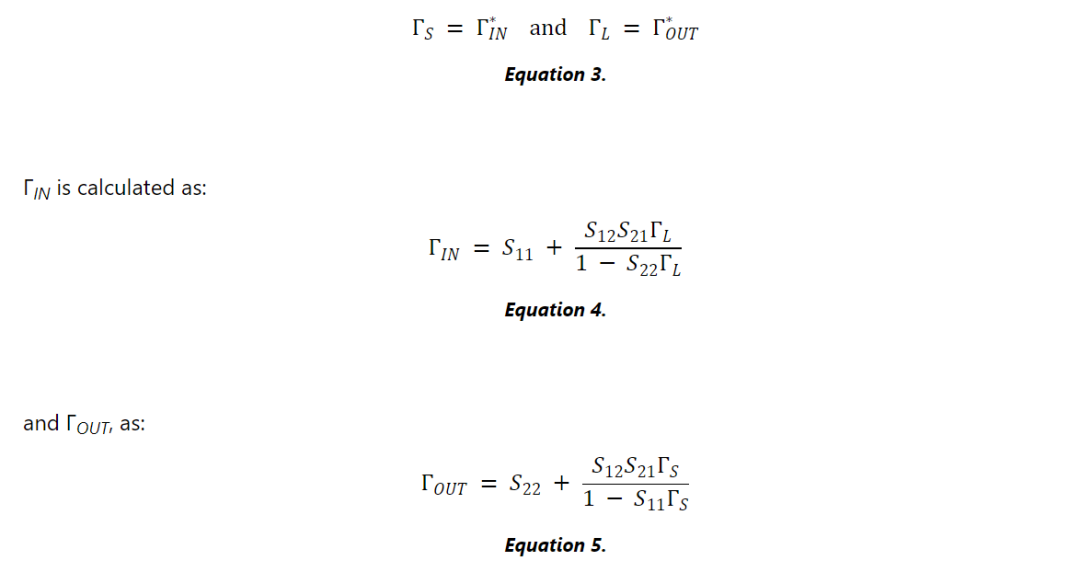
双边设计变得更加复杂的是双边设备的输入和输出端口之间存在交互。因此，方程 3 中提供的两个条件是耦合的，并且必须同时求解方程 3 中的两个表达式才能找到适当的 Г S和 Г L。

最大增益的单边设计实际上是双边方法的一种特例，其中S 12设置为零，解耦输入和输出方程，并且将Γ IN和Γ OUT分别简化为S 11和S 22。

双边放大器中同时共轭匹配的Г S和 Г L可以使用以下两个方程找到：

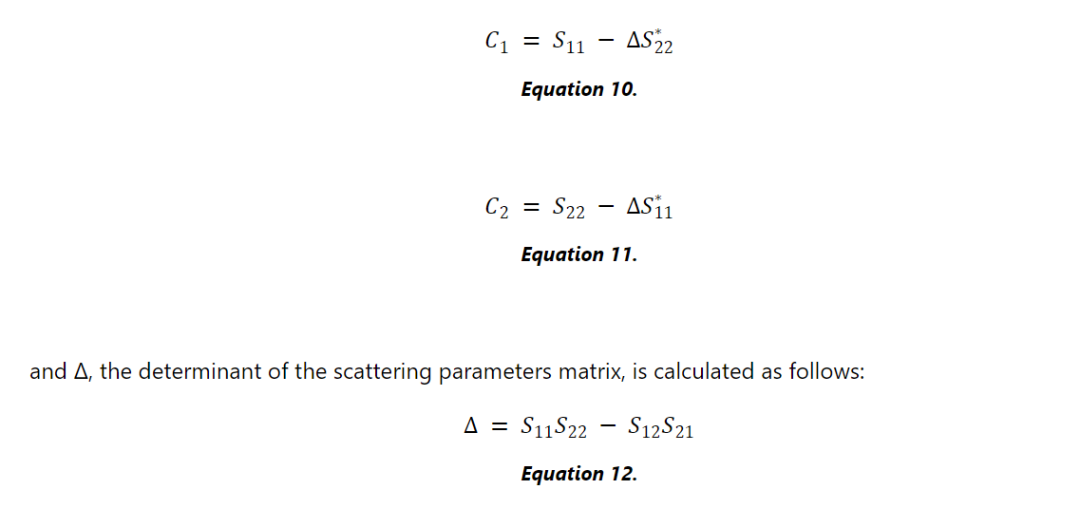
上述方程对于无条件稳定的设备是有效的。无条件稳定的器件始终可以共轭匹配以获得最大增益。如果设备可能不稳定，我们可以稳定它，然后找到同时共轭匹配条件的终止点。同时共轭匹配设备的最大传感器增益 ( GT ,max ) 由下式给出：

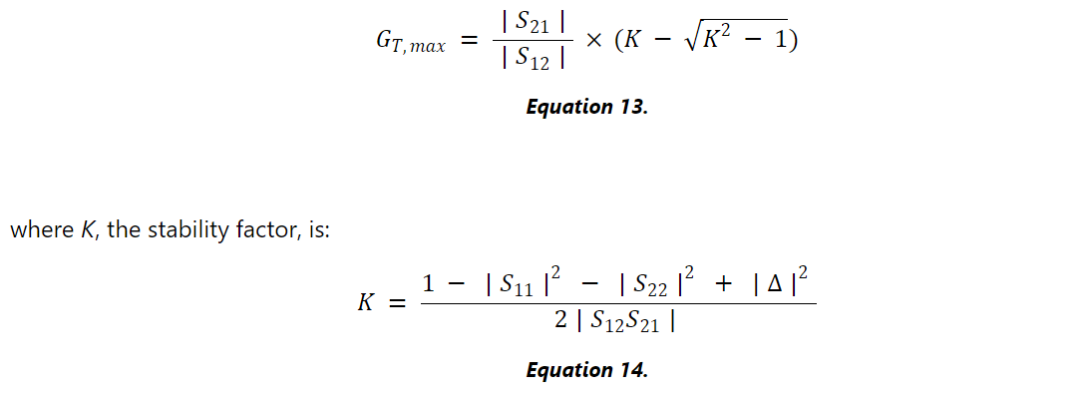
最大稳定增益

最大稳定增益 (MSG) 定义为K = 1 时的G T,max值。从公式 13 可以得出：

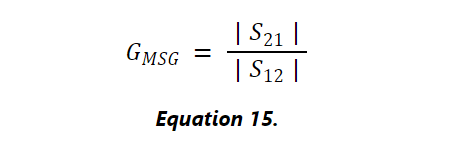
K = 1 代表临界稳定性，G MSG是我们将潜在不稳定的设备稳定到该点后获得的增益。这个增益量可以让我们比较不同器件在稳定工作条件下的增益。晶体管数据表通常在晶体管稳定的频率点提供 GT,max，在器件可能不稳定的频率点提供G MSG 。数据表通常还会以G MSG和GT ,max与频率的关系图的形式提供此信息，如图 4 所示。

请注意，在同时共轭匹配条件下，可用增益 ( G A ) 和传感器增益 ( G T ) 相等。在图 4 中，该增益项标记为 MAG（最大可用增益）。该图表明该器件在低于约 1.5 GHz 时可能不稳定。

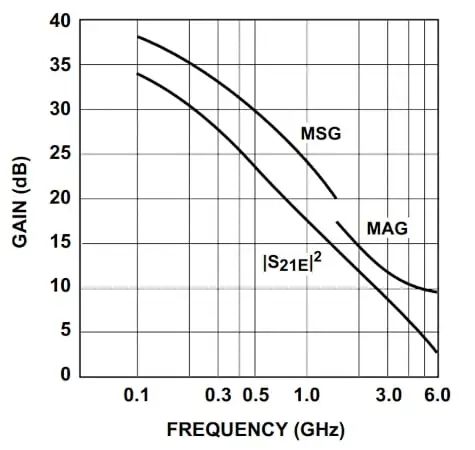
图 4. RF 晶体管数据表中的典型 MAG（ GA ,max 或GT ,max ）和 MSG 曲线。图片由惠普提供

实际上，可实现的 MSG 可能比公式 15 提供的值小 2 到 3 dB。这是因为实际设计并未在稳定性边界使用该器件，而是稍微使其过度稳定。实际增益降低的另一个原因是匹配网络等中使用的组件不可避免的损耗。

示例 2：计算最大传感器增益

假设晶体管的Z 0 = 50 Ω，其 S 参数如下表所示。

表 1.示例晶体管的 S 参数。

f (GHz)	小号11	S 21	S 12	S 22
0.8	0.440∠–157.6	4.725∠84.3	0.06∠55.4	0.339∠–51.8
1.4	0.533∠176.6	2.800∠64.5	0.06∠58.4	0.604∠–58.3
2.0	0.439∠159.6	2.057∠49.2	0.17∠58.1	0.294∠–68.1

我们的目标是确定f = 1.4 GHz 时的最大传感器增益。我们将通过查找该频率下同时共轭匹配条件的Г S和 Г L值来实现此目的。

首先，我们看看是否可以考虑设备单边。如果我们使用公式 1 计算f = 1.4 GHz时的单边品质因数，我们得到的值为U = 0.12。这意味着单边近似的误差较大，需要采用双边方法。

接下来，我们需要验证晶体管是否无条件稳定。为此，我们使用方程 12 和 14 来计算 Δ 和K；如果 |Δ|< 1 并且K大于 1，则设备在该频率下无条件稳定。在 f = 1.4 GHz 时，晶体管确实是无条件稳定的，因此我们可以找到满足同时共轭匹配条件的Г S和 Г L值。如果晶体管仅在f = 1.4 GHz 时无条件稳定，我们仍然可以使用双边设计方程，但我们必须检查获得的 Г S和 Г L值是否处于所有频率下的稳定工作区域。但是，您可以验证该晶体管对于表 1 中的所有三个频率都是无条件稳定的。 

对于可能不稳定的设备，另一种选择是首先稳定设备，然后将双边设计方程应用于新稳定设备的 S 参数。在f = 1.4 GHz时应用公式 6 和 7 ，我们得到 Г S = 0.83 ∠ –177.66 和 Г L = 0.85 ∠ 57.51。代入K = 1.12，| S 21 |=2.8，并且| S 12 |=0.06 代入方程 13 得出最大换能器增益GT ,max = 28.73，即 14.58 dB。使用Z史密斯圆图可以轻松确定匹配网络。

对于输入匹配部分，我们在史密斯圆图上找到 Γ S ，并通过沿常数 | Г S |旋转 180 度找到其相关的归一化导纳 ( y S ) 。圆圈。y S点的归一化导纳约为 10 + j 2，如图 5 所示。

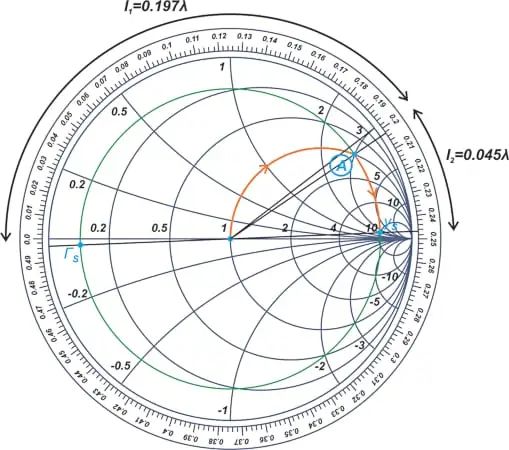
图 5.史密斯圆图显示示例晶体管的常数Γ S圆。 图片由 Steve Arar 提供

从现在开始，我们将史密斯圆图解释为Y史密斯圆图。我们想要一个从图表中心（或 50 Ω 终端）到y S的电路。常数 | Г S |的交点 与 (1 + jB ) 圆的圆被标记为点A，并且电纳为j 3 。

为了产生这种电纳，我们向 50 Ω 终端添加一个长度为l 1 = 0.197λ 的并联开路短截线。然后，我们添加一条长度为l 2 = 0.045λ 的串联线，以沿着常数 |Γ S |行进。绕y S。输出匹配部分可以类似的方式设计；图 6 中的史密斯圆图显示了详细信息。

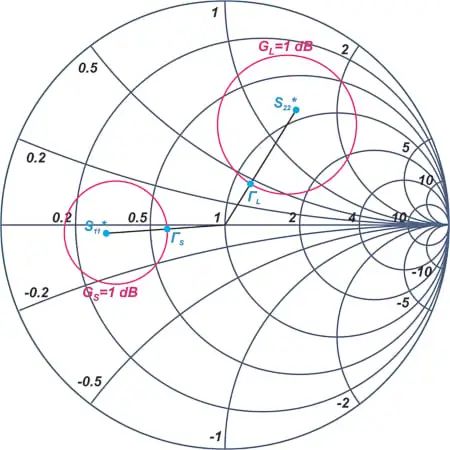
图 6.史密斯圆图显示示例晶体管的常数Γ L圆。 图片由 Steve Arar 提供

图 7 显示了最终的输入匹配部分。正如您所看到的，我们需要一个长度为l 3 = 0.203λ的开路短截线和一条长度为l 4 = 0.214λ 的串联线。

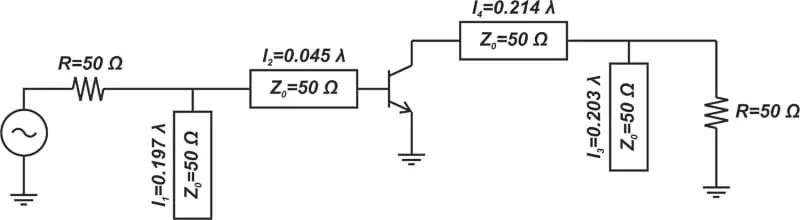
图 7. RF 放大器的输入匹配部分。图片由 Steve Arar 提供

图 8 显示了放大器的模拟增益，该增益非常接近 G T,max = 14.58 dB 的计算值。

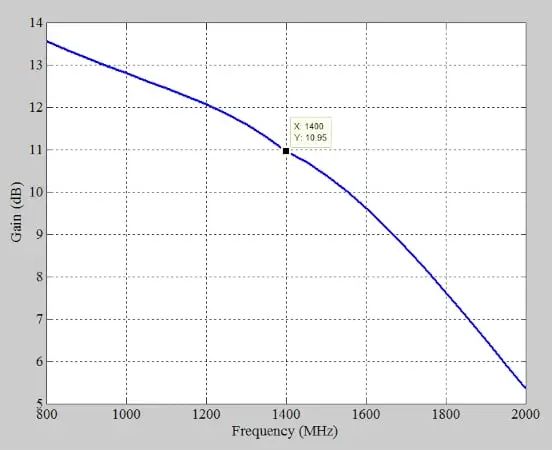
图 8.示例 RF 放大器的模拟增益。图片由 Steve Arar 提供

图 9 显示了放大器的输入反射系数。输入与 50 Ω 源阻抗匹配良好。

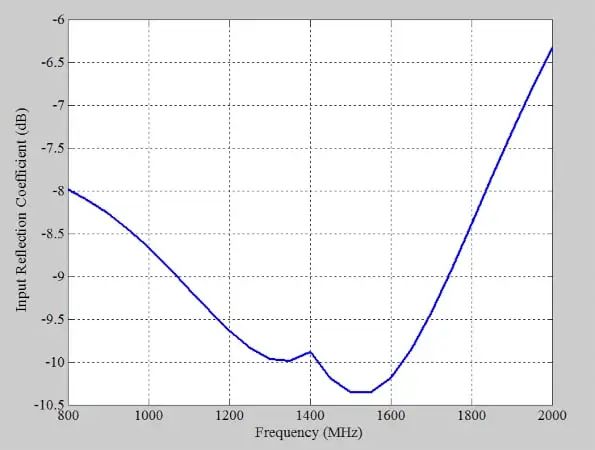
图 9.放大器的输入反射系数。图片由 Steve Arar 提供

在上述模拟中，软件提供了 0.8、1.4 和 2 GHz 的 S 参数。任何其他所需频率点的S参数可以通过插值获得。

概括

我们在本文中介绍了很多材料。以下是主要要点：

单边品质因数U使我们能够评估晶体管的反向增益是否可以忽略不计。

如果U小于0.1，则单边法的误差小于约±1dB。

对于较高的U值，建议使用双边设计，以考虑器件输入和输出端口之间的相互作用。

无条件稳定的器件始终可以设计用于同时共轭匹配，从而最大化增益。

如果器件可能不稳定，我们可以使用稳定技术来稳定器件，然后找到同时共轭匹配条件的终止点。

　　审核编辑：汤梓红