

卡尔曼滤波算法的基本原理
描述
卡尔曼滤波(Kalman Filter)是一种递归的、自适应的滤波算法,广泛应用于估计系统状态和观测过程中的噪声。它最初在1960年被提出,被认为是控制理论和信号处理领域中最重要的发展之一。卡尔曼滤波器在许多领域,包括导航、机器人、金融和通信系统中都有广泛的应用。
1,基本原理:
卡尔曼滤波器的核心思想是融合系统的动态模型和实际的观测数据,通过对过程和测量噪声的估计,提供对系统状态的最优估计。其基本原理可以分为两个步骤:预测(Predict)和更新(Update)。
预测(Predict):
在预测阶段,卡尔曼滤波器使用系统的动态模型,以及先前的状态估计来预测系统的下一个状态。这一过程基于系统的状态方程和控制输入,考虑系统的动态演变。预测的结果是对系统状态的先验估计,其中考虑了系统的动态行为。卡尔曼滤波的状态方程通常表示为:
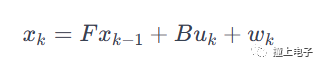
其中,Xk是系统状态向量,F 是状态转移矩阵,B 是输入矩阵,Uk是控制输入向量,Wk是过程噪声。
更新(Update):
在更新阶段,卡尔曼滤波器使用实际的测量数据来校正先前的状态估计。这一过程基于测量方程和测量噪声,考虑了观测到的系统输出。更新的结果是对系统状态的后验估计,其中融合了测量信息。
卡尔曼滤波的测量方程通常表示为:
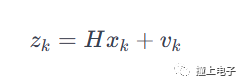
其中,Zk是测量向量,H是测量矩阵,Vk测量噪声。
2,状态估计的迭代过程:
卡尔曼滤波是一个迭代的过程,其更新步骤依赖于预测和测量的相互作用。以下是卡尔曼滤波的迭代过程:
初始化: 首先,需要初始化卡尔曼滤波器的状态估计(X0)和协方差矩阵(P0)
预测: 使用系统的状态方程进行状态的预测,并更新状态的协方差矩阵。这一步考虑了系统的动态演变和过程噪声。其中,Xk是先验状态估计,Pk是先验协方差矩阵,Q是过程噪声协方差矩阵。
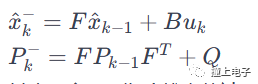
测量更新: 使用测量方程将预测的状态与实际的测量数据进行比较,从而校正状态估计,并更新协方差矩阵。这一步考虑了观测到的系统输出和测量噪声。其中,Kk 是卡尔曼增益,R是测量噪声协方差矩阵,Xk 是后验状态估计,Pk 是后验协方差矩阵。
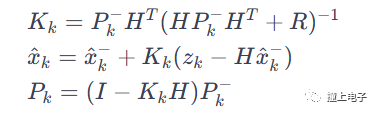
重复: 重复预测和测量更新步骤,将后验状态估计作为下一步的先验状态估计,持续迭代。
3,关键概念:
卡尔曼增益: 卡尔曼增益是一个关键的概念,它决定了预测和测量更新之间的相对权重。卡尔曼增益越大,系统对测量数据的依赖性越强,反之亦然。
协方差矩阵: 协方差矩阵描述了状态估计的不确定性。通过在迭代过程中更新协方差矩阵,卡尔曼滤波器能够动态调整对状态估计的信任程度。
过程噪声和测量噪声: 过程噪声和测量噪声是卡尔曼滤波中的两个关键参数,它们用于描述系统动态模型和测量过程中的不确定性。适当估计和调整这些噪声是卡尔曼滤波器性能的关键。
4,示例代码:
#include < stdio.h >
// 定义状态向量的维度
#define STATE_DIM 2
// 定义测量向量的维度
#define MEASURE_DIM 1
// 定义卡尔曼滤波器结构体
typedef struct {
// 状态估计向量
float x[STATE_DIM];
// 状态协方差矩阵
float P[STATE_DIM][STATE_DIM];
// 过程噪声协方差矩阵
float Q[STATE_DIM][STATE_DIM];
// 测量噪声协方差矩阵
float R[MEASURE_DIM][MEASURE_DIM];
// 状态转移矩阵
float F[STATE_DIM][STATE_DIM];
// 测量矩阵
float H[MEASURE_DIM][STATE_DIM];
} KalmanFilter;
// 初始化卡尔曼滤波器
void kalmanFilterInit(KalmanFilter *kf, float initialX, float initialP);
// 卡尔曼滤波预测步骤
void kalmanPredict(KalmanFilter *kf, float controlInput);
// 卡尔曼滤波更新步骤
void kalmanUpdate(KalmanFilter *kf, float measurement);
int main() {
// 初始化卡尔曼滤波器
KalmanFilter kf;
kalmanFilterInit(&kf, 0.0, 1.0);
// 模拟输入数据
float controlInput = 0.1;
float measurementNoise = 0.5;
// 模拟10次迭代
for (int i = 0; i < 10; ++i) {
// 预测步骤
kalmanPredict(&kf, controlInput);
// 模拟测量
float trueMeasurement = 2.0 * kf.x[0] + measurementNoise;
// 更新步骤
kalmanUpdate(&kf, trueMeasurement);
// 打印结果
printf("Iteration %d - True Value: %f, Estimated Value: %fn", i + 1, trueMeasurement, kf.x[0]);
}
return 0;
}
// 初始化卡尔曼滤波器
void kalmanFilterInit(KalmanFilter *kf, float initialX, float initialP) {
// 初始化状态估计向量
kf- >x[0] = initialX;
kf- >x[1] = 0.0;
// 初始化状态协方差矩阵
kf- >P[0][0] = initialP;
kf- >P[0][1] = 0.0;
kf- >P[1][0] = 0.0;
kf- >P[1][1] = initialP;
// 初始化过程噪声协方差矩阵
kf- >Q[0][0] = 0.001;
kf- >Q[0][1] = 0.0;
kf- >Q[1][0] = 0.0;
kf- >Q[1][1] = 0.001;
// 初始化测量噪声协方差矩阵
kf- >R[0][0] = 0.01;
// 初始化状态转移矩阵
kf- >F[0][0] = 1.0;
kf- >F[0][1] = 1.0;
kf- >F[1][0] = 0.0;
kf- >F[1][1] = 1.0;
// 初始化测量矩阵
kf- >H[0][0] = 1.0;
kf- >H[0][1] = 0.0;
}
// 卡尔曼滤波预测步骤
void kalmanPredict(KalmanFilter *kf, float controlInput) {
// 预测状态估计
kf- >x[0] = kf- >F[0][0] * kf- >x[0] + kf- >F[0][1] * kf- >x[1] + controlInput;
// 预测状态协方差矩阵
kf- >P[0][0] = kf- >F[0][0] * kf- >P[0][0] * kf- >F[0][0] + kf- >F[0][1] * kf- >P[1][0];
kf- >P[0][1] = kf- >F[0][0] * kf- >P[0][1] * kf- >F[0][1] + kf- >F[0][1] * kf- >P[1][1];
kf- >P[1][0] = kf- >F[1][0] * kf- >P[0][0] * kf- >F[0][0] + kf- >F[1][1] * kf- >P[1][0];
kf- >P[1][1] = kf- >F[1][0] * kf- >P[0][1] * kf- >F[0][1] + kf- >F[1][1] * kf- >P[1][1] + kf- >Q[1][1];
}
// 卡尔曼滤波更新步骤
void kalmanUpdate(KalmanFilter *kf, float measurement) {
// 计算卡尔曼增益
float K[STATE_DIM][MEASURE_DIM];
float S;
// 计算卡尔曼增益
S = kf- >H[0][0] * kf- >P[0][0] * kf- >H[0][0] + kf- >R[0][0];
K[0][0] = kf- >P[0][0] * kf- >H[0][0] / S;
K[1][0] = kf- >P[1][0] * kf- >H[0][0] / S;
// 更新状态估计
kf- >x[0] = kf- >x[0] + K[0][0] * (measurement - kf- >H[0][0] * kf- >x[0]);
kf- >x[1] = kf- >x[1] + K[1][0] * (measurement - kf- >H[0][0] * kf- >x[0]);
// 更新状态协方差矩阵
kf- >P[0][0] = (1 - K[0][0] * kf- >H[0][0]) * kf- >P[0][0];
kf- >P[0][1] = (1 - K[0][0] * kf- >H[0][0]) * kf- >P[0][1];
kf- >P[1][0] = -K[1][0] * kf- >H[0][0] * kf- >P[0][0] + kf- >P[1][0];
kf- >P[1][1] = -K[1][0] * kf- >H[0][0] * kf- >P[0][1] + kf- >P[1][1];
}
卡尔曼滤波的优势在于它能够提供对系统状态的最优估计,同时适应于线性和高斯噪声的系统。然而,卡尔曼滤波也有一些限制,例如对非线性系统的适应性较差,且需要对系统动态模型和噪声参数进行良好的估计。
-
卡尔曼滤波在机器人导航中的应用2024-12-16 1859
-
卡尔曼滤波算法c语言实现方法2024-01-17 4934
-
卡尔曼滤波的原理和C代码2023-12-07 4732
-
卡尔曼滤波算法对比其他的滤波算法有什么优点?2023-10-11 822
-
卡尔曼滤波器的基本原理2022-03-21 6761
-
卡尔曼滤波简介2022-02-28 2135
-
卡尔曼滤波的基本原理及应用2020-05-05 1470
-
基于SOM降阶卡尔曼滤波算法在组合导航上的应用2017-11-05 1363
-
LabVIEW一维卡尔曼滤波算法2017-10-21 11451
-
卡尔曼滤波算法2016-12-17 1120
-
图书分享:卡尔曼滤波算法的几何解释2015-06-11 13546
-
卡尔曼滤波2013-07-04 3058
-
卡尔曼滤波算法的改进方案2011-06-14 1767
全部0条评论

快来发表一下你的评论吧 !

