为什么天线阵列中相邻两个天线之间的距离常使用半波长？

我们回顾一下信号到达角度的计算：

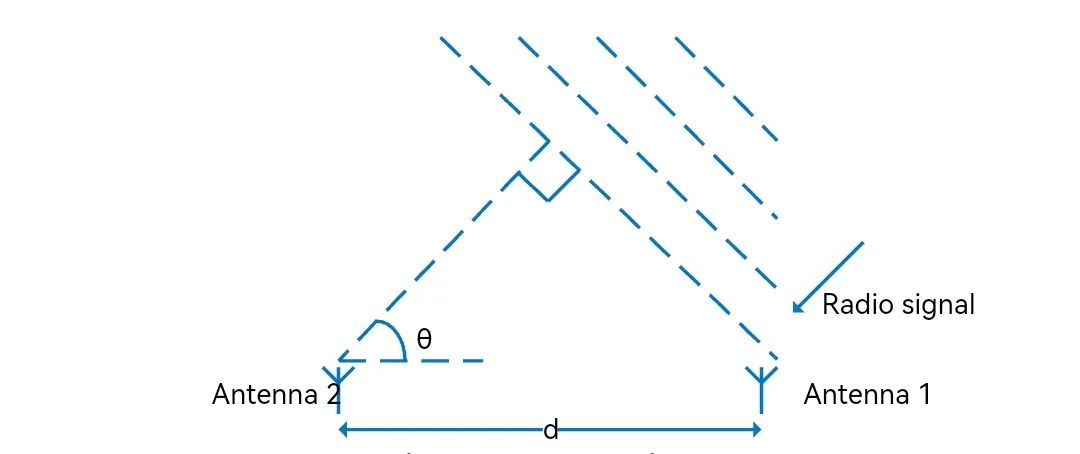
如信号到达角度为θ，两根天线距离为d，两根天线上信号到达的时间差:

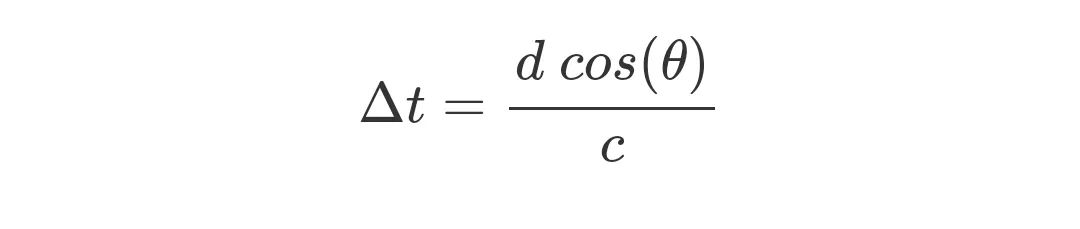
由于时间差产生的相位差:

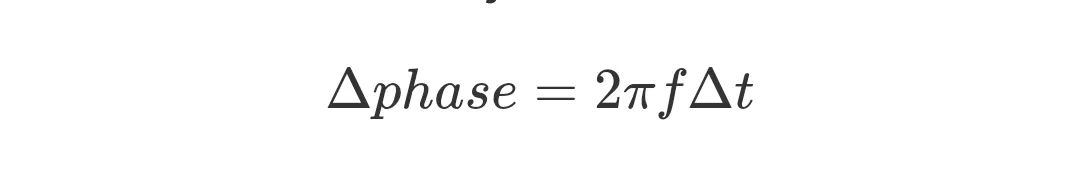
通过测量相位差，可以得到信号到达角度:

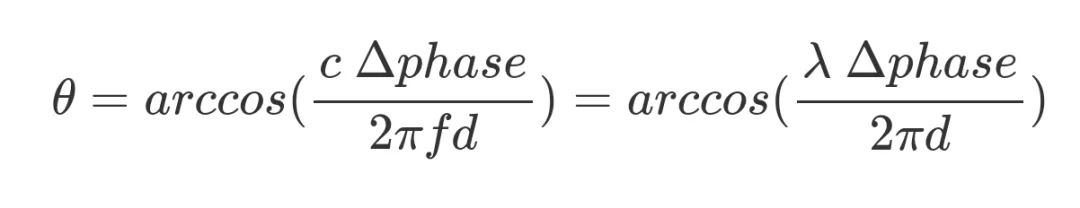
由于相位差是在-π到π之间，所以要求: 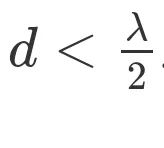那么当 d 不是λ/2 时，会出现什么样的情况呢？ 我们一直使用天线之间的距离d等于半波长。但有时候，阵列可能无法实现精确的N/2间隔，例如当空间受到限制时，或者当同一阵列必须在各种载波频率上工作时。 下图演示了d在λ/2和4λ之间改变示意图。我们删除了极坐标图的下半部分，因为下半部分和上半部分对称。

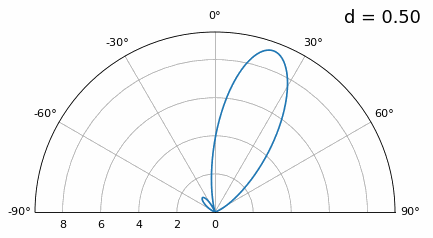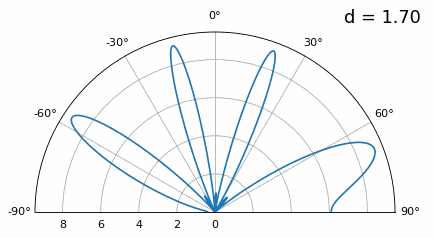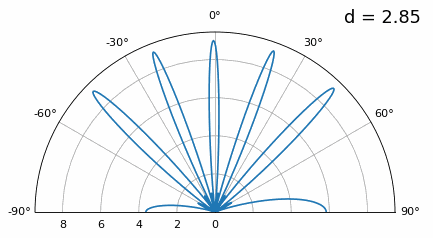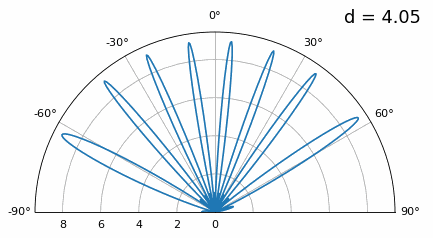
  如你所看到的，除了我们之前讨论的180度歧义之外，我们现在还有额外的歧义，并且随着d变高(额外/不正确的波瓣形成)，情况会变得更糟。这些额外的波瓣被称为光栅波瓣，它们是“空间混叠”的结果。 现在，当 d 小于 λ/2 时会发生什么，例如当我们需要将阵列拟合在狭小空间中时？让我们重复相同的模拟：

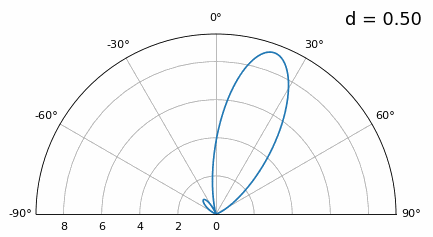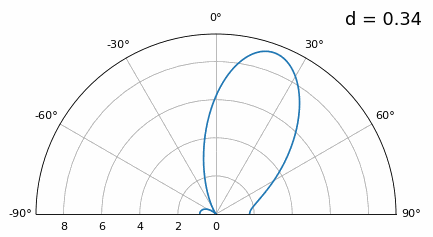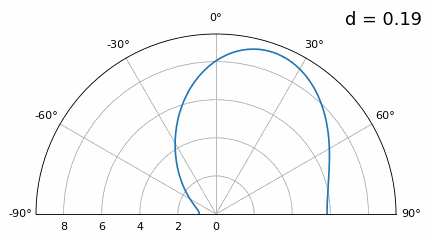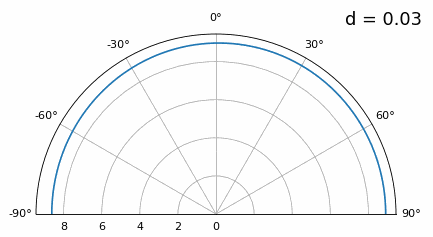
  虽然主瓣随着 d 变低而变宽，但它的最大值仍然是 20 度，并且没有光栅瓣，因此理论上这仍然有效（至少在高 SNR 下）。为了更好地理解当 d 变得太小时会发生什么，让我们重复实验，但有一个来自 -40 度的额外信号：  

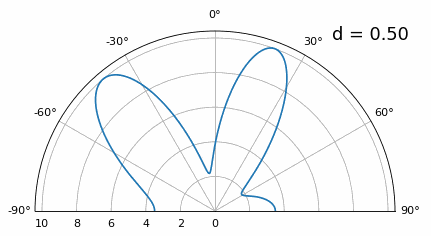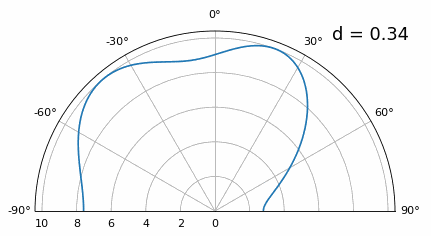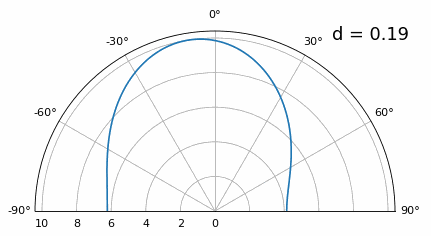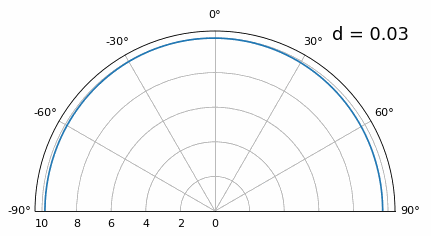
  一旦我们低于 λ/4，两条不同的路径之间就没有区别了，数组的性能很差。   波束形成技术方法非常简单，但其准确性通常不是很好，虽然有一些波束成形技术可以提供比传统波束成形更精确的波束，但仍要求保持 d 尽可能接近 λ/2 。