

大规模神经网络优化:超参最佳实践与规模律
描述
从理论分析入手把握大规模神经网络优化的规律,可以指导实践中的超参数选择。反过来,实践中的超参数选择也可以指导理论分析。本篇文章聚焦于大语言模型,介绍从 GPT 以来大家普遍使用的训练超参数的变化。
规模律研究的是随着神经网络规模的增大,超参数、性能是如何改变的。规模律是对模型、数据、优化器关系的深刻刻画,揭示大模型优化时的普遍规律。通过规模律,我们可以用少量成本在小模型上验证超参数的选择和性能的变化情况,继而外推到大模型上。
在 LLM 中规模性常常变换模型大小和数据规模,进行大量调参而保持优化器不变。故对于大模型优化器而言,规模性是其性能很好的展现(性能上限)。设计更好的优化器(用更少的数据达到相同的性能)就是在挑战现有的规模律。


神经网络规模律
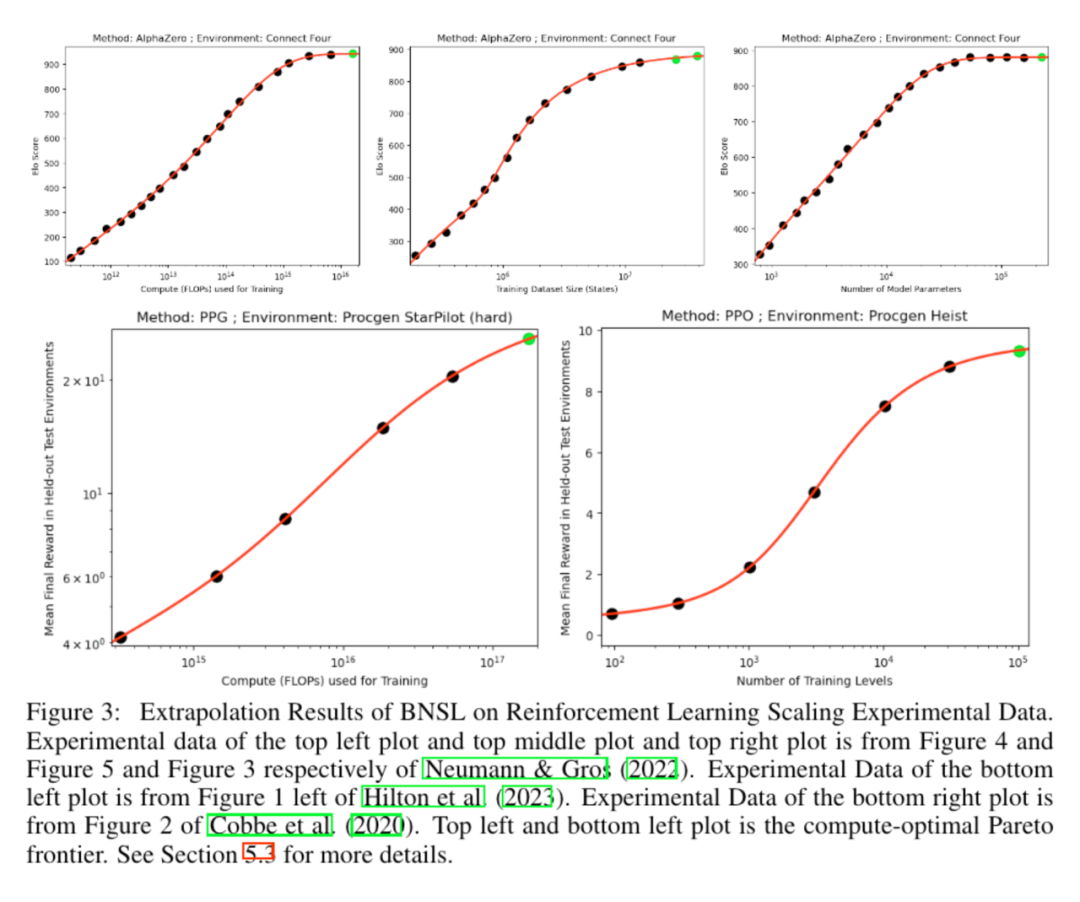
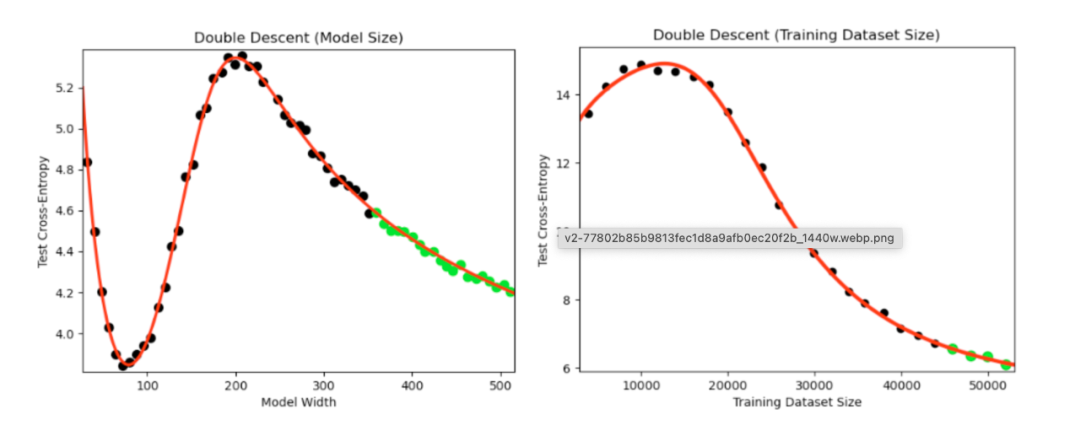
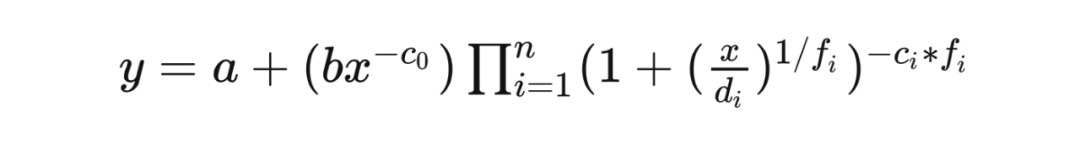
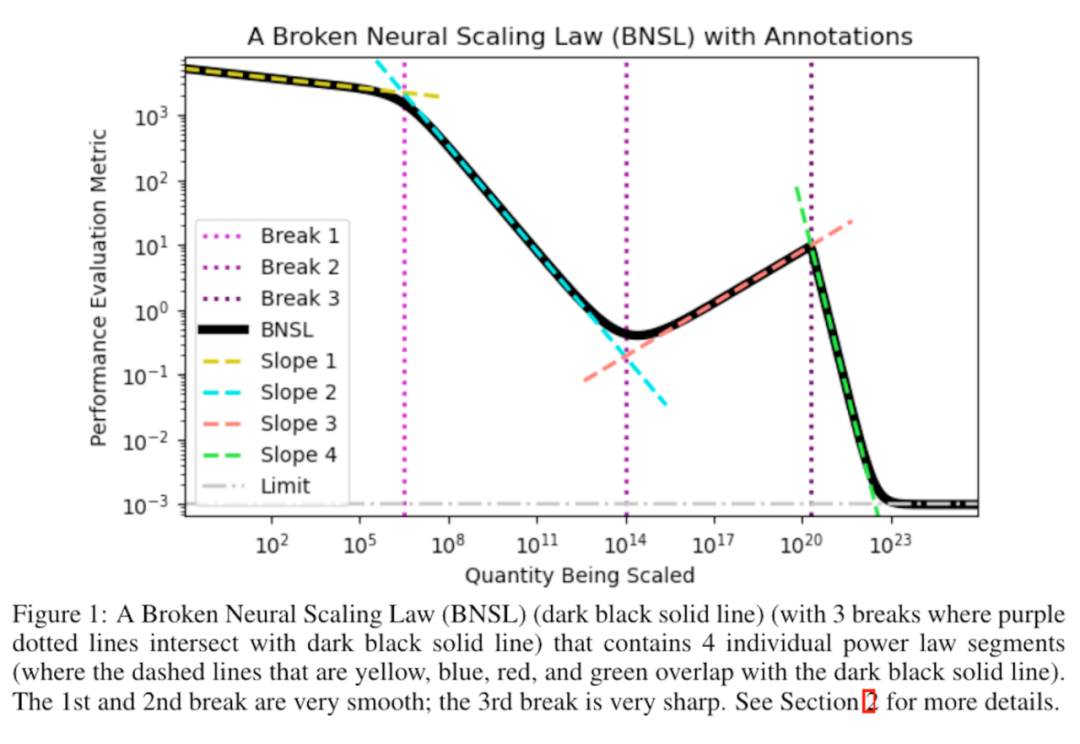

大语言模型规模律
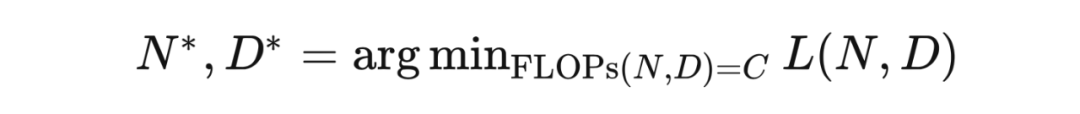
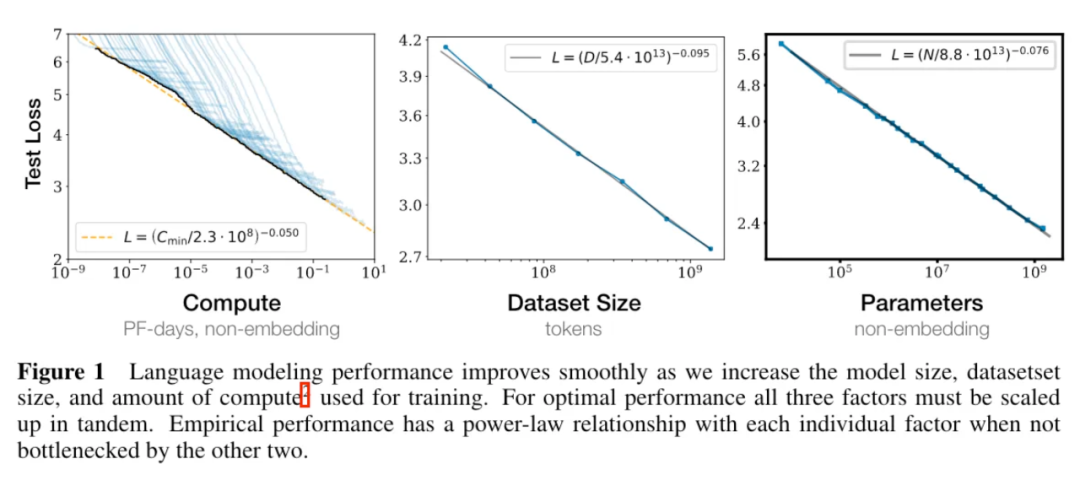
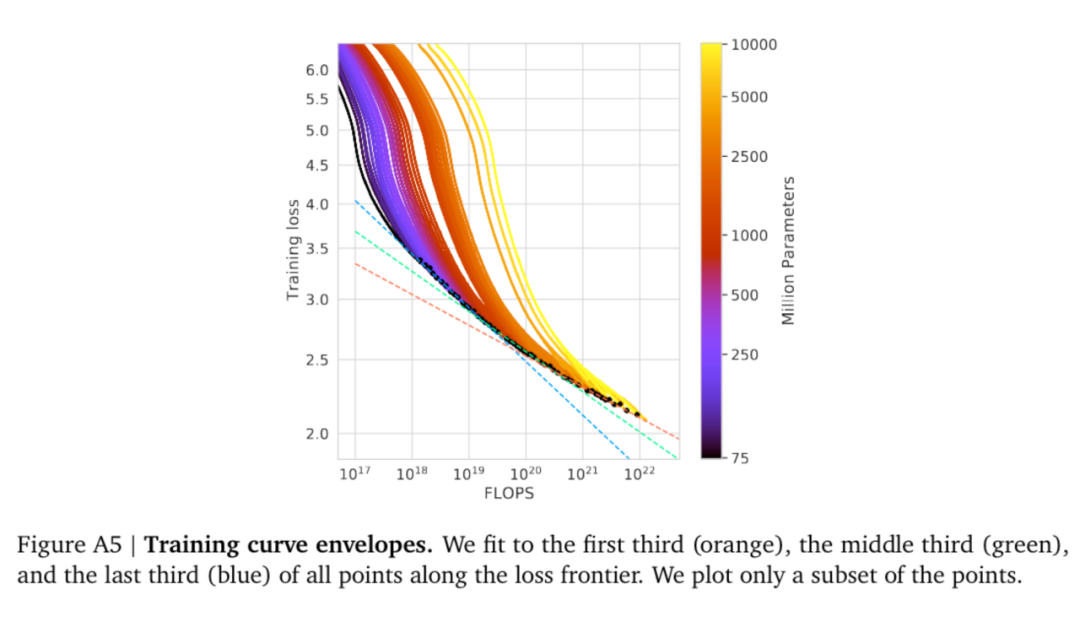
对不同的 没有尝试使用不同的学习率调整策略(正确的学习率调整策略对训练影响很大) [KMH+20] 使用的 较小。规模性存在曲率,导致用太小的 得到的结论不准确。(规模性存在曲率也说明了最终该规律会失效)
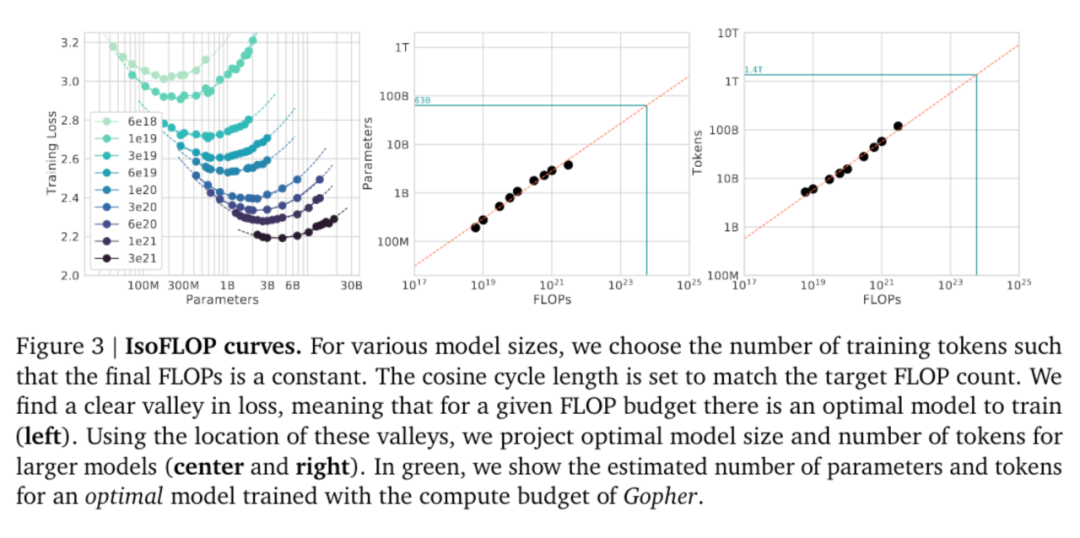
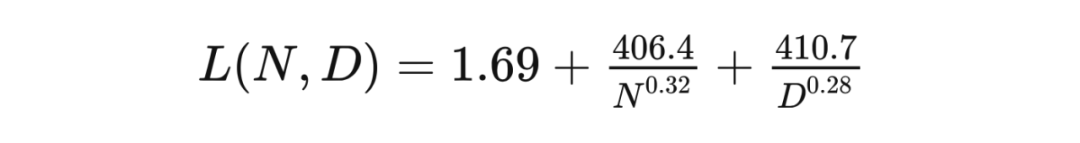
5. 模型的迁移泛化能力与在训练数据集上的泛化能力正相关。
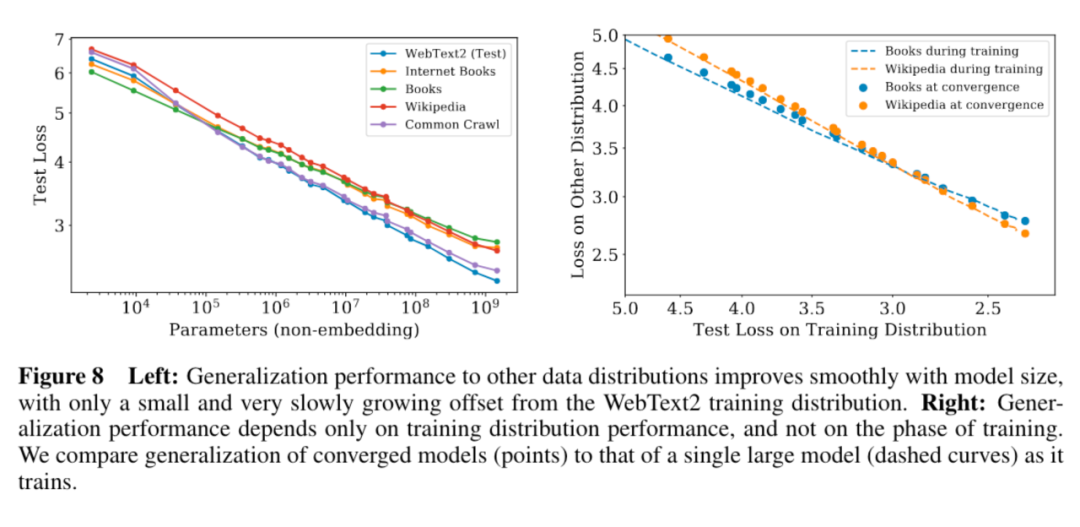
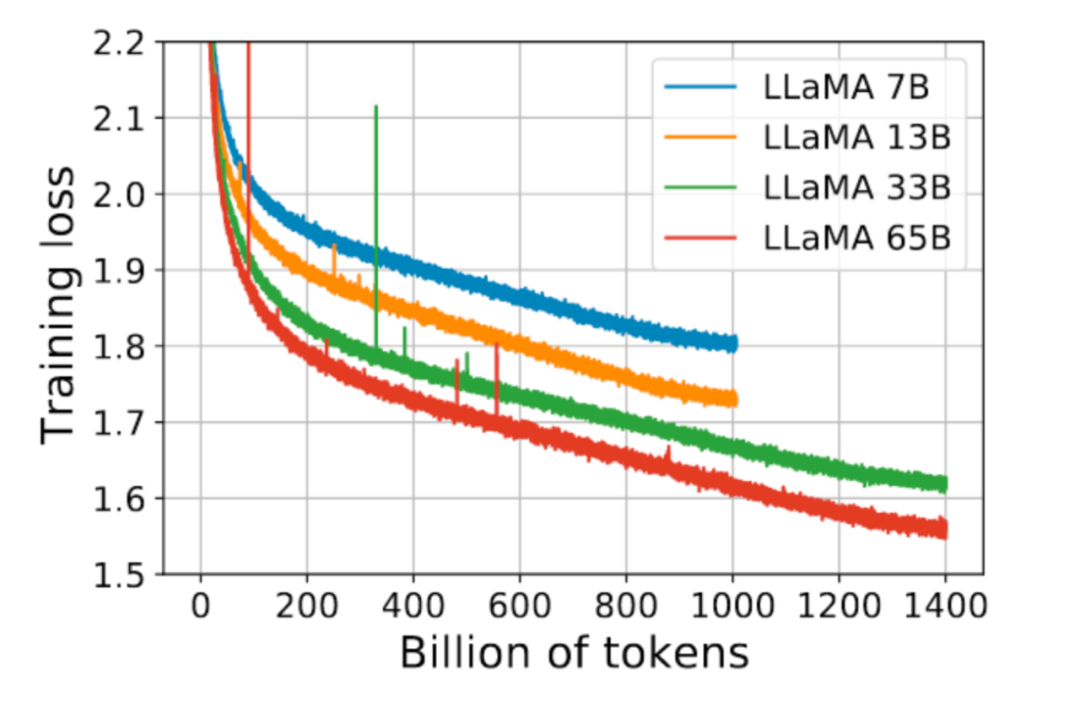
6. 更大的模型收敛更快(更少的数据量达到相同的损失)
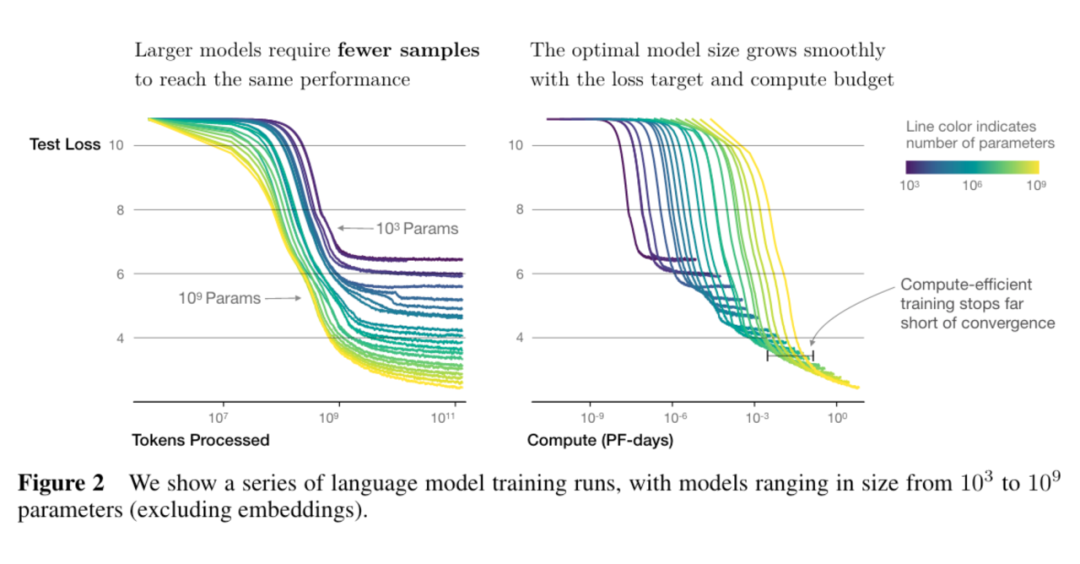

大语言模型规模律拾遗
3.1 涌现是指标选择的结果,连续指标与参数规模符合幂律分布
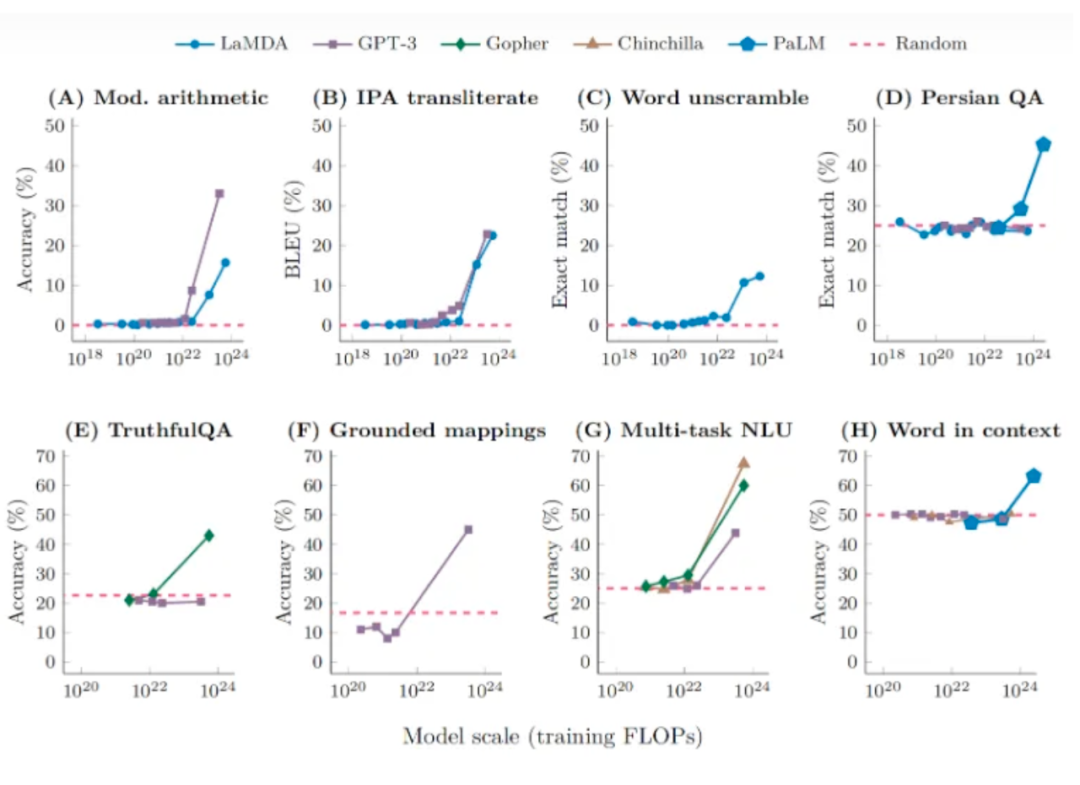
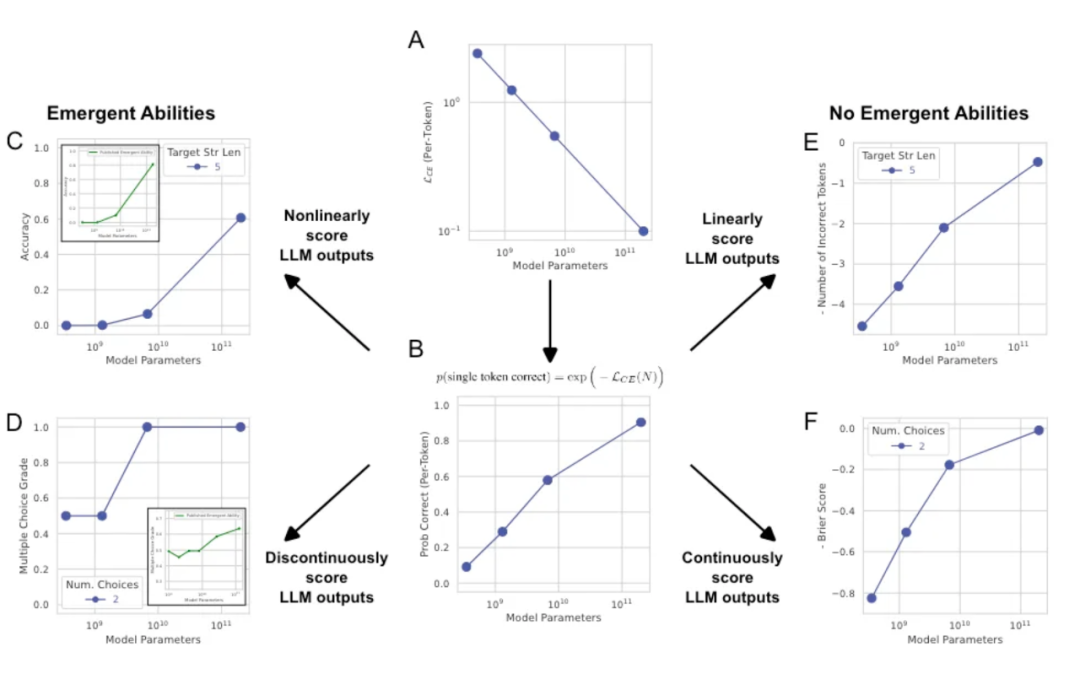
3.2 大模型需要更小的学习率
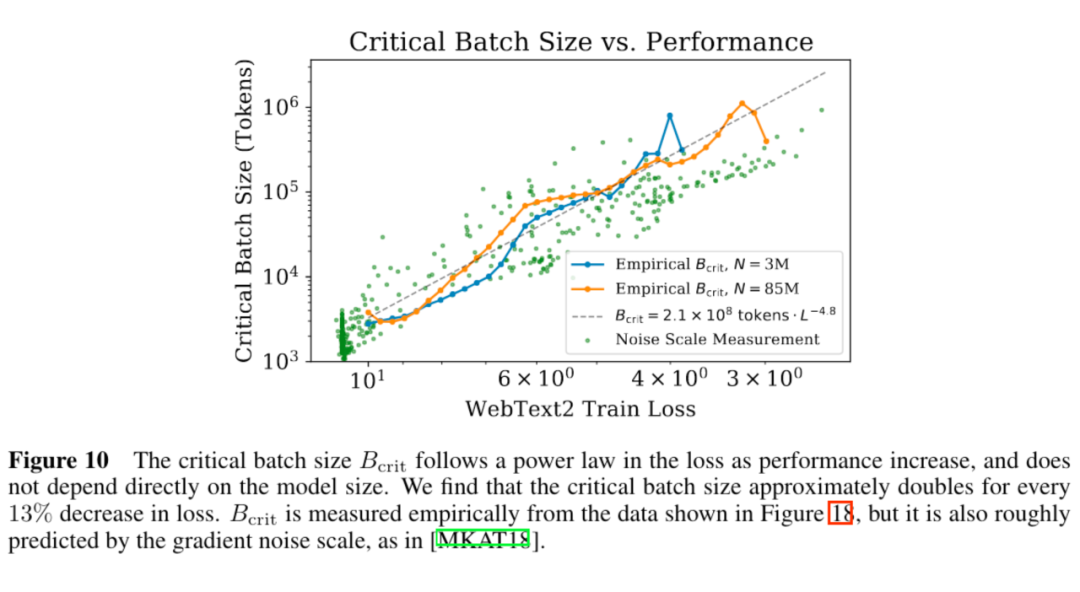
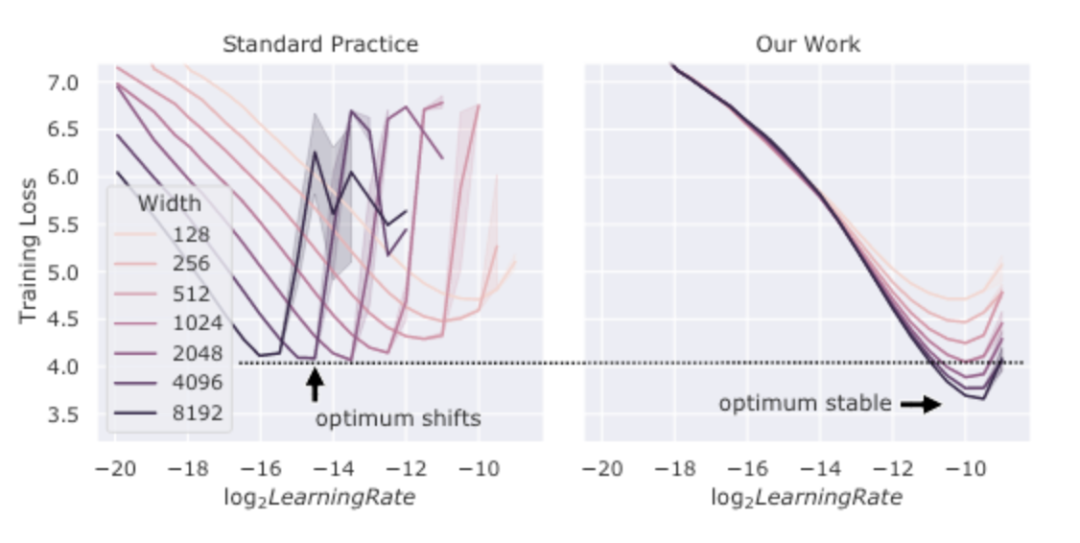
通过上文中的大模型参数经验,我们很容易就发现大模型需要更小的学习率。[YHB+22] 在下左图中展示了这点。其认为这是为了控制总方差在一定值(方差随参数量以 增大)。对于这点笔者暂未找到详细的理论解释。[YHB+22] 中还提出了一种新的初始化和参数设置方法以保证不同规模的模型可以使用相同的学习率,这里不再展开。
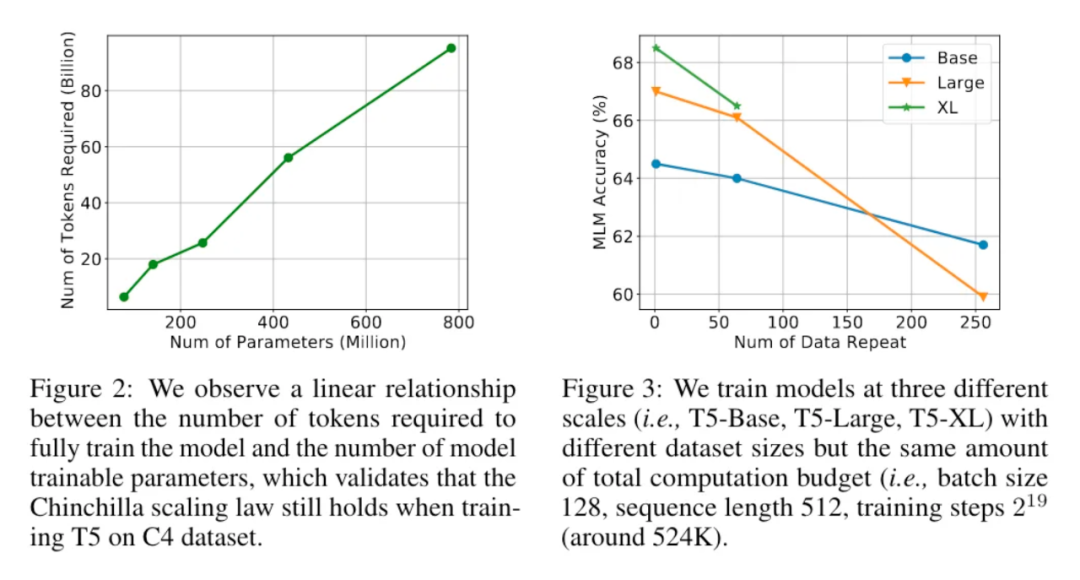
3.3 使用重复数据训练时(multi-epoch),应该用更多的轮次训练较小的模型
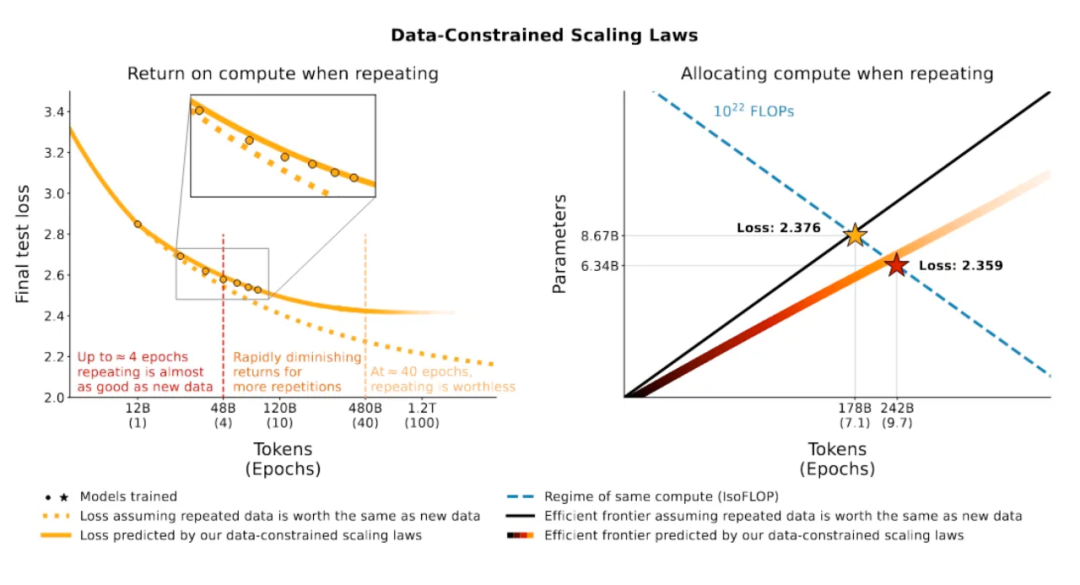
3.4 使用重复数据训练对训练帮助很小
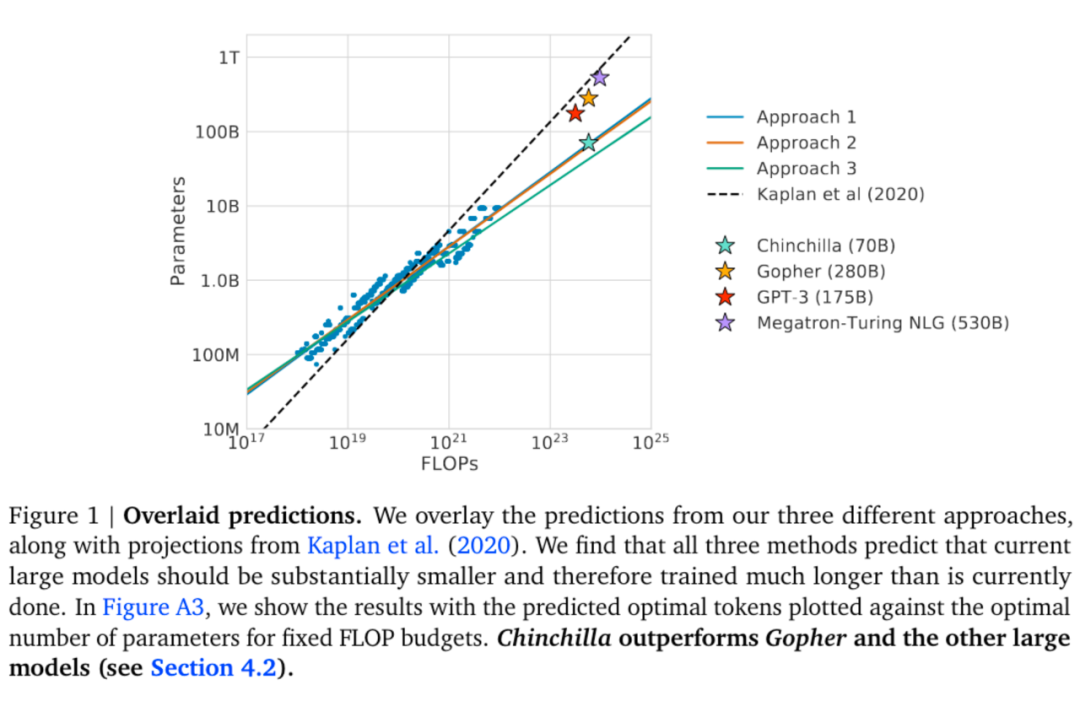
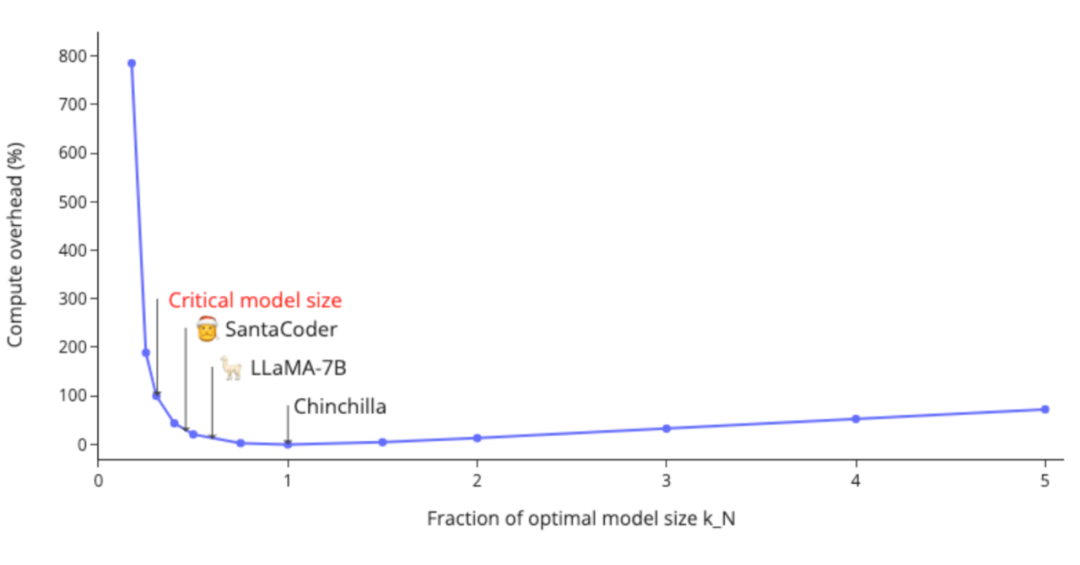
3.5 训练比 Chinchilla 规模律更小的模型
Chinchilla 规模律的出发点是给定计算量,通过分配参数量和数据量最小化损失值。换言之,给定要达到的损失值,最小化计算量。然而在实际中,训练一个小模型能带来计算量(代表训练开销)以外的收益:
小模型部署后进行推理成本更小 小模型训练所需的集群数量更少
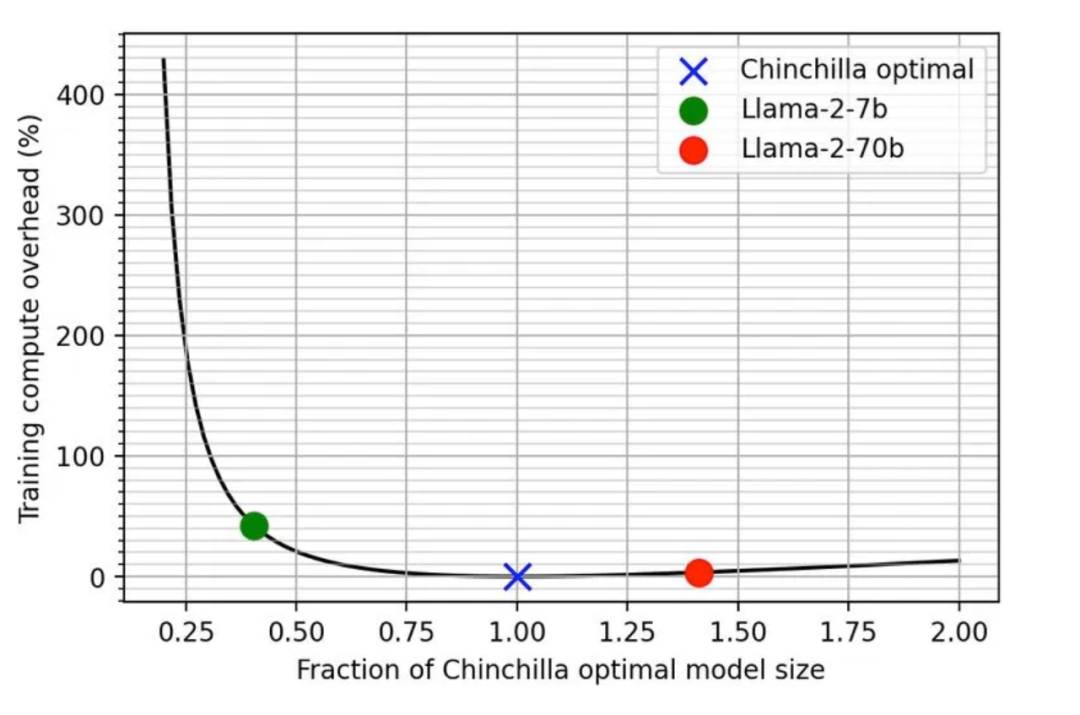
训练所需的数据量不够(正如 [XFZ+23] 指出的,我们正在用尽互联网上所有的 tokens)。 小集群上训练小模型需要更长的训练时间(Llama2 500k its);如果使用大集群训练则更困难(比如要使用更大的批量大小才能提高效率)。

LLM 的超参选择
4.1 GPT(117M):
Adam lr:2.5e-4 sch: warmup linear 2k, cosine decay to 0 bs: 32k=64x512 its: 3M (100e) L2: 0.01 init: N(0, 0.02)
Adam(0.9,0.999) lr: 1e-4 sch: warmup 10k, linear decay to 0 bs: 128k=256x512 its: 1M (40e) L2: 0.01 dropout: 0.1
4.3 Megatron-LM(GPT2 8.3B & Bert 3.9B):
Adam lr: 1.5e-4 sch: warmup 2k, cosine decay to 1e-5 bs: 512k=512x1024 its: 300k L2: 0.01 dropout: 0.1 gradient norm clipping: 1.0
AdaFactor lr: 1e-2 sch: warmup constant 10k, sqrt decay bs: 65k=128x512 its: 500k (1e)
Adam(0.9, 0.95, eps=1e-8) lr & final bs: 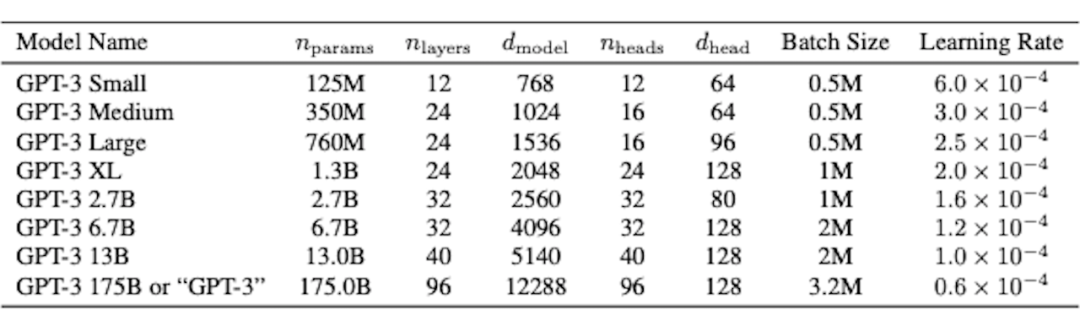
sch: warmup linear 375m tokens, cosine decay to 0.1xlr 260b tokens, continue training with 0.1xlr bs sch: 32k to final bs gradually in 4-12B tokens seq length: 2048 data: 680B gradient norm clipping: 1.0
Adam (Adafactor unstable beyond 7.1B) lr & final bs: 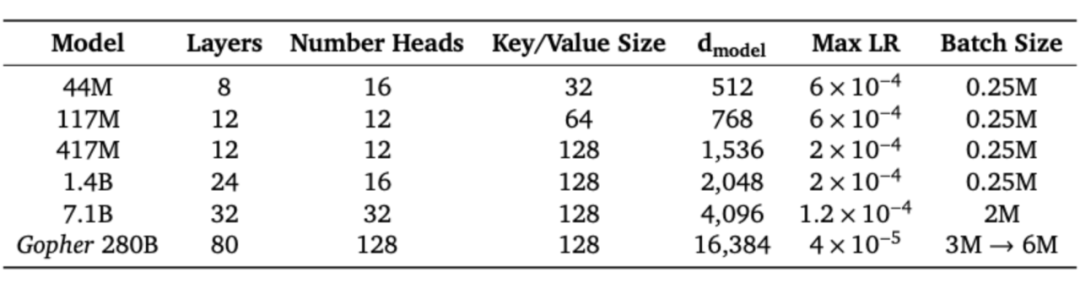
sch: warmup 1.5k, cosine decay to 0.1xlr gradient norm clipping: 0.25 for 7.1B & 280B, 1.0 for the rest
AdamW lr: 1e-4 bs: 1.5M to 3M others follow Gopher
Adam(0.9, 0.95) (SGD plateau quickly) lr & bs: 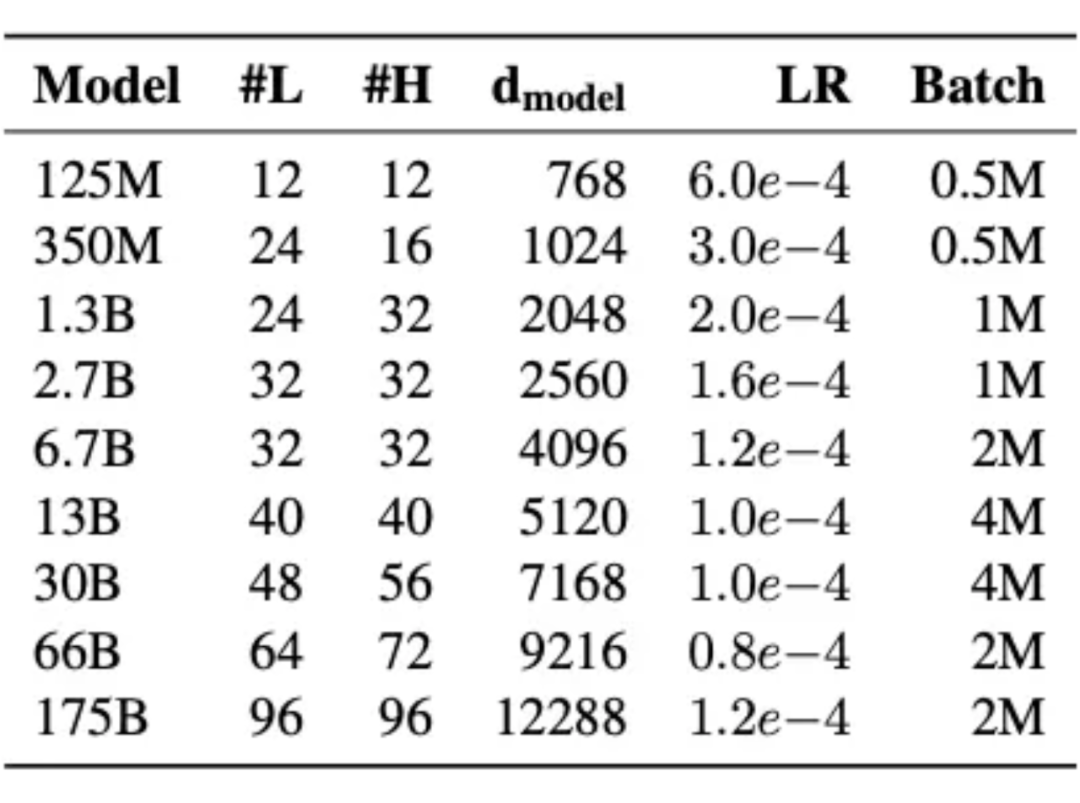
sch: warmup linear 2k, decay to 0.1xlr L2: 0.1 dropout: 0.1 gradient norm clipping: 1.0 init: N(0, 0.006), output layer N(0, 0.006* )
Adafactor(0.9, 1-) lr 1e-2
bs: 1M (<50k), 2M (<115k), 4M (<255k)
dropout: 0.1 gradient norm clipping: 1.0 its: 255kinit: N(0, embedding N(0,1)
AdamW(0.9, 0.95) lr & bs: 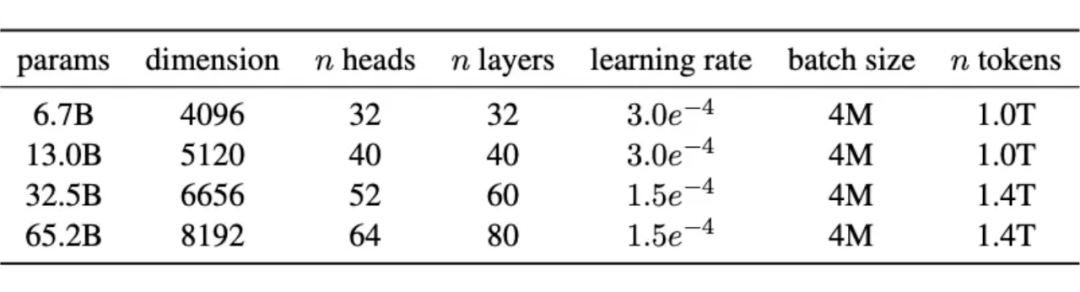
sch: warmup 2k, decay to 0.1xlr L2: 0.1 gradient norm clipping: 1.0
AdamW(0.9, 0.95, eps=1e-5) lr 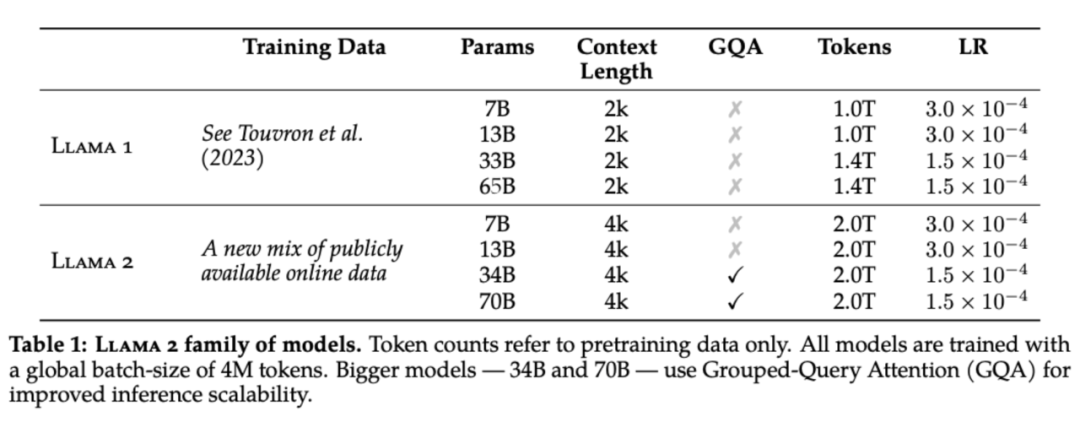
sch: warmup 2k, decay to 0.1xlr L2: 0.1 gradient norm clipping: 1.0
参考文献
[ADV+23] Why do we need weight decay in modern deep learning?
[CGR+23] Broken neural scaling laws
[HBM+22] Training Compute-Optimal Large Language Models
[KMH+20] Scaling Laws for Neural Language Models
[SMK23] Are Emergent Abilities of Large Language Models a Mirage?
[YHB+22] Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer
[MRB+23] Scaling Data-Constrained Language Models
[XFZ+23] To Repeat or Not To Repeat: Insights from Scaling LLM under Token-Crisis
[H23] Go smol or go home
原文标题:大规模神经网络优化:超参最佳实践与规模律
文章出处:【微信公众号:智能感知与物联网技术研究所】欢迎添加关注!文章转载请注明出处。
- 相关推荐
- 热点推荐
- 物联网
-
智能手机跑大规模神经网络的主要策略2018-05-07 4019
-
大规模特征构建实践总结2018-11-19 2800
-
基于赛灵思FPGA的卷积神经网络实现设计2019-06-19 4092
-
大规模MIMO的性能2019-07-17 2440
-
如何利用SoPC实现神经网络速度控制器?2019-08-12 3042
-
解析深度学习:卷积神经网络原理与视觉实践2020-06-14 3430
-
改善深层神经网络--超参数优化、batch正则化和程序框架 学习总结2020-06-16 1493
-
如何构建神经网络?2021-07-12 1862
-
基于RBF神经网络的通信用户规模预测模型2017-11-22 1224
-
面向大规模图像分类的深度卷积神经网络的优化2017-12-15 971
-
加快部署 5G 基站的最佳实践:RF 前端大规模 MIMO 入门2022-12-26 2679
-
卷积神经网络和深度神经网络的优缺点 卷积神经网络和深度神经网络的区别2023-08-21 5023
-
韩国开发出大规模人工神经网络硬件技术2024-01-26 1133
-
如何训练和优化神经网络2024-07-01 1446
-
BP神经网络的调参技巧与建议2025-02-12 1561
全部0条评论

快来发表一下你的评论吧 !

