什么是光学中的近场和远场？二者的区别是什么？

近场和远场在不同的光学范畴有不同的定义，需要加以区分。下面从菲涅尔数入手，通过菲涅尔数介绍二者的区别。  

衍射光学

首先介绍菲涅尔数（Fresnel number）:

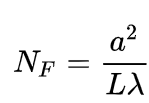
其中，a 是通光孔径，L 是探测器位置距孔径的距离。lambda 是波长。

当菲涅尔数远小于1时，为夫琅禾费衍射（Fraunhofer diffraction），即远场衍射。例如在如通常的成像光学中聚焦位置所发展的衍射，即艾里斑（ Airy diffraction pattern）：  

圆形孔径的艾里斑（from wikipedia）   当菲涅尔数远大于1时，为菲涅尔衍射（Fresnel diffraction），即近场衍射。由于探测器非常接近衍射发生的位置（如小孔），这时候波前形状对衍射的影响不可忽略。对于同样的圆形孔径，其近场衍射图案为：  

圆形孔径的菲涅尔衍射（from wikipedia）   关于菲涅尔衍射的一个著名案例是泊松亮斑（Poisson spot）：  

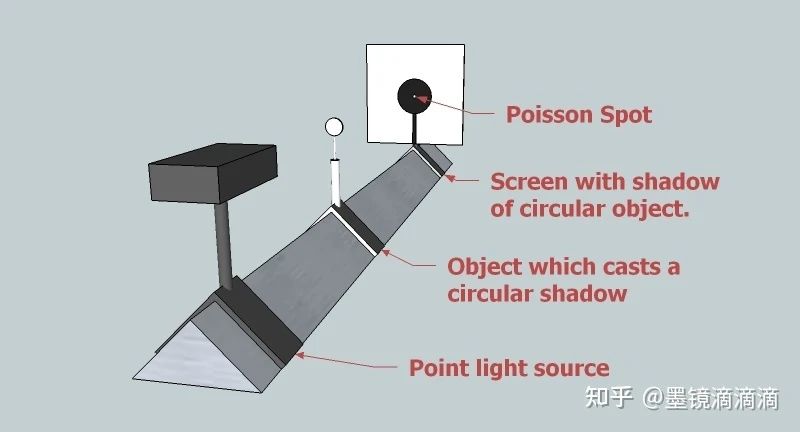
泊松亮斑实验（from wikipedia）   需注意的是，衍射在此种情况下发生于物体外沿，因此菲涅尔数公式中的 a 可视为无穷大，即满足近场衍射条件。

若无衍射发生，即根据几何光学，探测器中间为纯黑色，但实际并未如此：  

泊松亮斑（from wikipedia）

激光束

在激光的空间传输或光纤输出端传输时，通常用高斯光束来描述: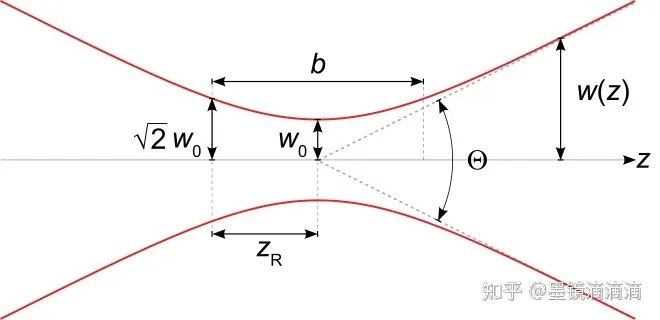



高斯光束

在瑞利范围（Rayleigh range）内通常被称为近场，远离瑞利范围时通常被称为远场。远场的光场分布通常可以由近场光场分布的二维傅里叶变换描述。  

审核编辑：刘清