

Python轴承故障诊断之经验模态分解EMD原理介绍
电子说
描述
1 经验模态分解EMD原理介绍
1.1 EMD概述
经验模态分解(Empirical Mode Decomposition,EMD)方法是一种自适应信号时频处理方法,特别适用于非线性、非平稳信号的分析处理[1]。其本质是一种对信号进行分解的方法,将信号分解为各个相互独立的成分的叠加,依据数据自身的时间尺度特征来进行信号分解,具备自适应性。
EMD的优点在于它是一种自适应的、数据驱动的分解方法,不需要预先假设信号的分布或结构。这使得它适用于处理各种类型的信号,包括非线性和非平稳信号。
EMD 认为任何一个复杂序列都是由多个单频率信号叠加而成,因此可以分解成若干个 本征模态函数(Intrinsic Mode Functions, IMF),IMF 的各个分量即代表了原始信号中的各频 率分量,并按照从高频到低频的顺序依次排列,这也是 IMF 的物理含义[2]。
1.2 本征模态函数IMF
本征模态函数(Intrinsic Mode Functions, IMF)就是原始信号被 EMD 分解之后得到的各层信号分量。任何信号都可以拆分成若干个 IMF 之和。IMF 有两个假设条件:
- 在整个数据段内,极值点的个数和过零点的个数必须相等或相差最多不能超过一 个;
- 在任意时刻,由局部极大值点形成的上包络线和由局部极小值点形成的下包络线 的平均值为零,即上、下包络线相对于时间轴局部对称。
对于上述的条件理解如下:
第一,图线要反复跨越 x 轴,比如:
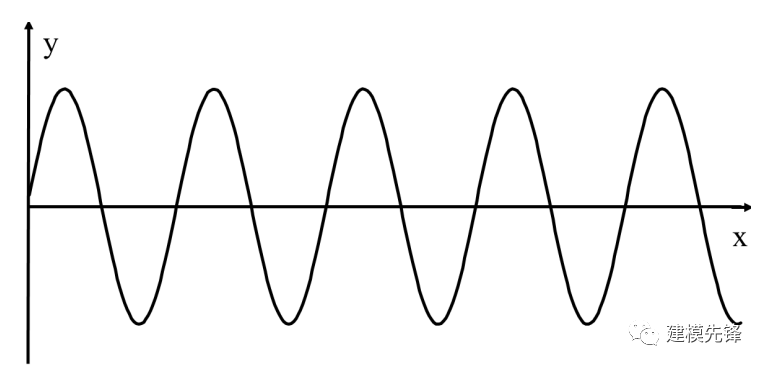
反复跨越 x 轴
而不能像下面这样某次穿过零点后出现多个极点:
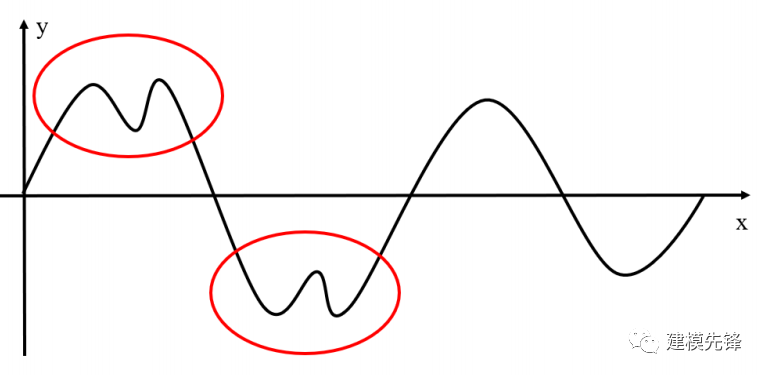
某次穿过零点后出现多个极点
第二,上下包络线要对称,比如:
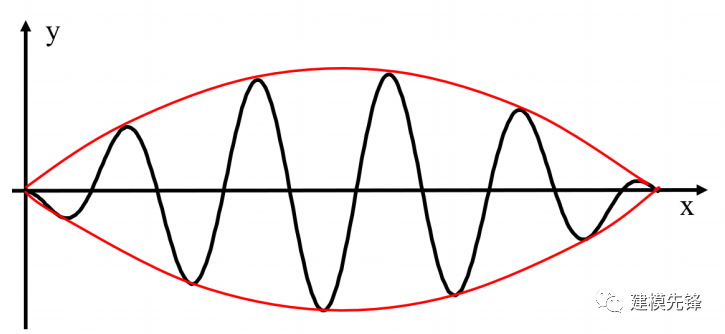
上下包络线对称
而不能像如下这样,上下包络线不对称
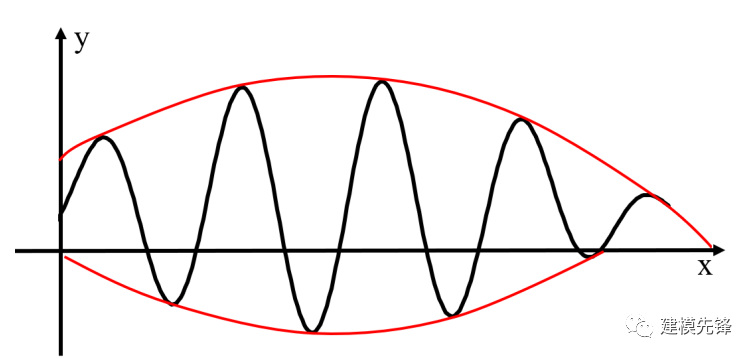
1.3 EMD 分解的基本假设
- 信号至少有两个极值点:一个极大值点和一个极小值点;
- 特征时间尺度由极值之间的时间间隔定义;
- 如果数据完全没有极值,但只包含拐点,那么可以一次或多次划分来揭示极值点,最终的结果可以通过积分得到
2 EMD分解的基本原理和步骤
EMD的分解过程是一个迭代的过程。首先,对原始信号进行极值点的提取,然后通过连接极值点的均值得到第一轮的近似IMF(也叫做“本征模态”)。接下来,将这个近似IMF从原始信号中减去,得到一个新的信号,然后对这个新信号再次进行极值点提取和均值连接,得到第二轮的近似IMF。如此往复,直到得到的近似IMF满足某种停止准则。
对于原始信号 X(t)
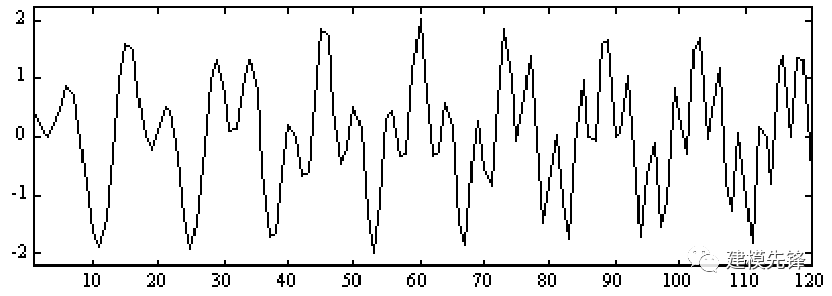
第一步,极值点提取:
从待分解的信号中识别局部极值点,包括局部极大值和局部极小值。极值点是信号中的局部特征,能够帮助刻画信号的振荡特性。
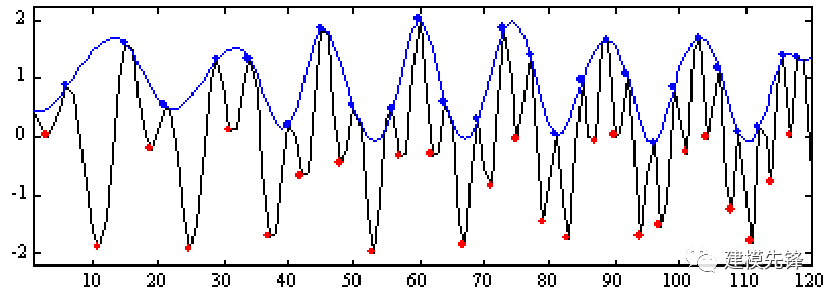
第二步,构建上下包络线:
通过连接相邻的局部极大值和局部极小值,构建信号的上包络线和下包络线。上包络线 U(t) 由局部极大值连接而成,下包络线 L(t) 由局部极小值连接而成。包络线用于描述信号的振荡范围。
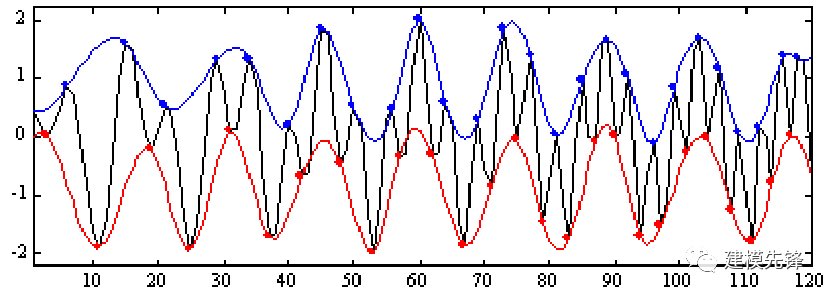
第三步,提取均值函数:
计算上包络线和下包络线的平均值,得到均值函数 m1。将原始信号减去均值函数,得到一维信号 h1。
m1 = ( U(t) + L(t) ) / 2
h1 = X(t) - m1
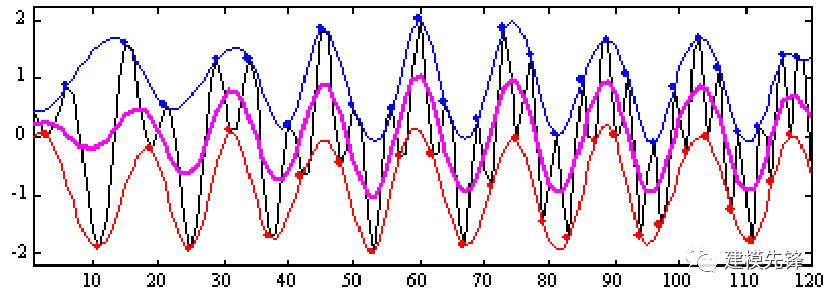
第四步,迭代分解:
对减去均值函数后的一维信号 h1,重复步骤1-3的过程,直到得到的剩余信号为“单调信号”,或者满足IMF的两个假设条件。迭代k次的IMF为
hk = h(k-1) - mk
第五步,确定本征模态函数(IMF):
在每一次迭代中,通过极值点提取、构建包络线等步骤,得到的剩余信号被称为一个本征模态函数(IMF)。IMF具有局部特征,并且代表了信号在不同尺度上的振荡模式。使用上述方法得到的第一个IMF记为c1, 然后将c1从原始信号中分离,得到
r1 = X(t) - c1
由于r1仍然包含大量信息,因此将r1作为新的原始信号,再通过步骤1-4的分析,可以得到IMF2,以此类推,得到
r1 - c2 = r2,... ..., r(n-1) -cn = rn
当cn或rn小于某一设定值,或者得到的剩余信号为“单调信号”,无法提取更多的IMF时,迭代终止,得到最终的分解结果为:
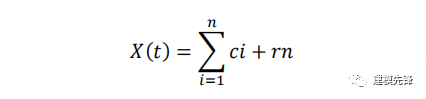
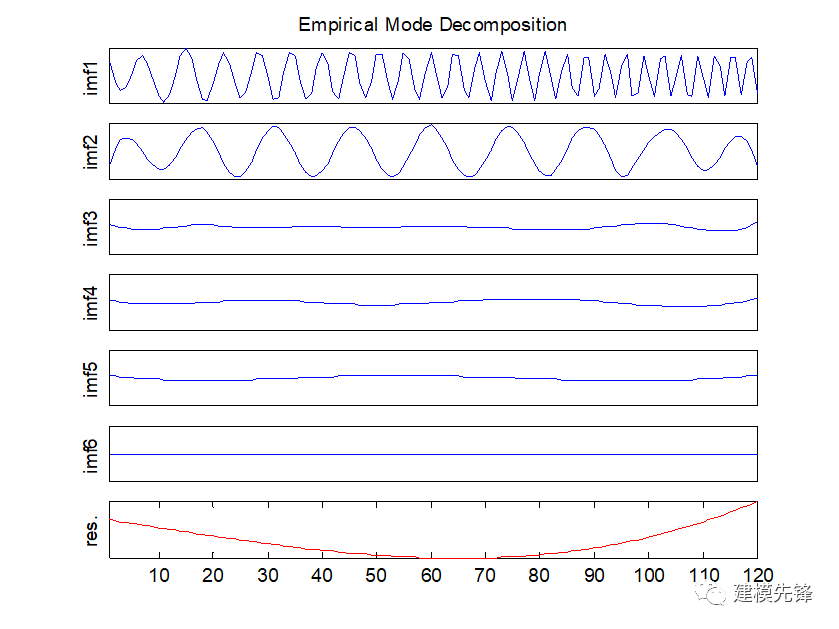
第六步,重构信号:
将得到的IMF函数进行逐个提取,直到无法再得到新的IMF为止。最终得到的IMF函数可以被看作是信号在不同时间尺度上的振荡模式,它们的组合可以重构原始信号。
这些基本步骤构成了EMD方法的核心流程,通过这些步骤,EMD可以将复杂的信号分解成不同尺度和频率的本征模态函数,从而揭示信号的局部特征和振荡模式。
3 基于Python的EMD实现
在 Python 中,使用 PyEMD 库来实现经验模态分解(EMD)
2.1 代码示例
import numpy as np
import matplotlib.pyplot as plt
from PyEMD import EMD
# 生成一个示例信号
t = np.linspace(0, 1, 1000)
s = np.sin(11*2*np.pi*t*t) + 6*t*t
# 创建 EMD 对象
emd = EMD()
# 对信号进行经验模态分解
IMFs = emd(s)
# 绘制原始信号和每个本征模态函数(IMF)
plt.figure(figsize=(15,10))
plt.subplot(len(IMFs)+1, 1, 1)
plt.plot(t, s, 'r')
plt.title("Original signal")
for num, imf in enumerate(IMFs):
plt.subplot(len(IMFs)+1, 1, num+2)
plt.plot(t, imf)
plt.title("IMF "+str(num+1))
plt.show()
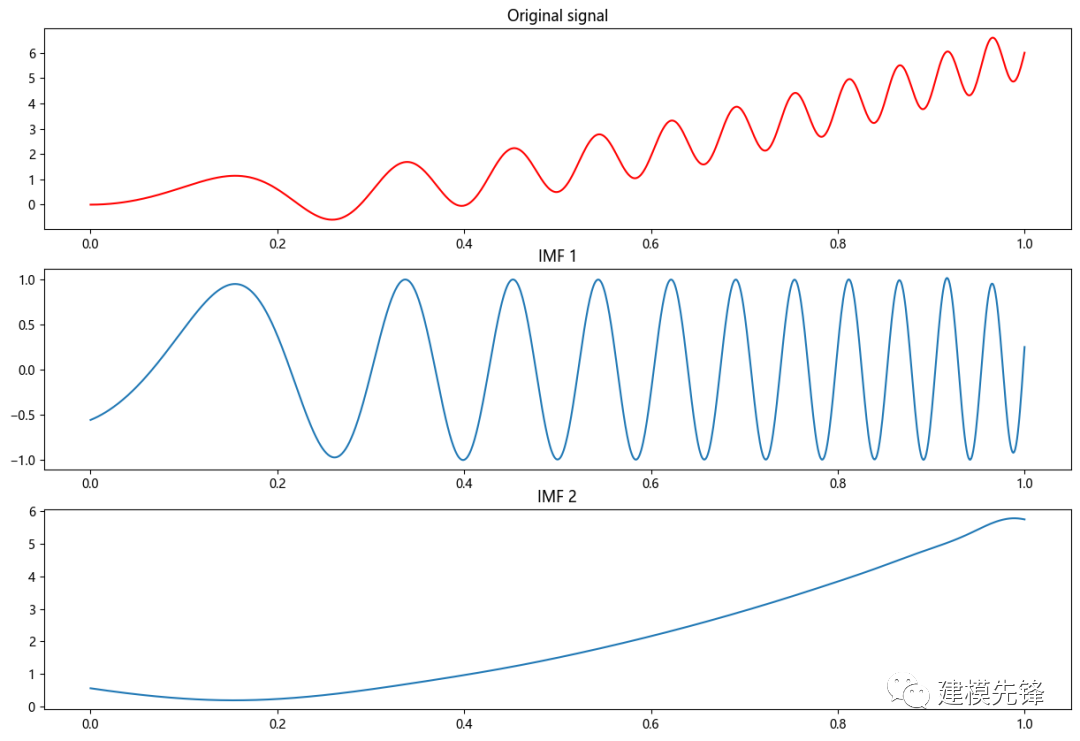
2.2 轴承故障数据的分解
选择 0.021英寸滚珠故障信号数据来做EMD分解
2.2.1 凯斯西储大学轴承数据的加载
第一步,导入包,读取数据
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')
# 读取MAT文件
data = loadmat('21_2.mat') # 0.021英寸 滚珠
# 注意,读取出来的data是字典格式,可以通过函数type(data)查看。
第二步,数据集中读取 驱动端加速度数据,取一个长度为1024的信号进行后续观察和实验
# DE - drive end accelerometer data 驱动端加速度数据
data_list = data['X222_DE_time'].reshape(-1)
# 划窗取值(大多数窗口大小为1024)
data_list = data_list3[0:1024]
# 进行数据可视化
plt.figure(figsize=(20,10))
plt.plot(data_list)
plt.title("滚珠")
plt.show()
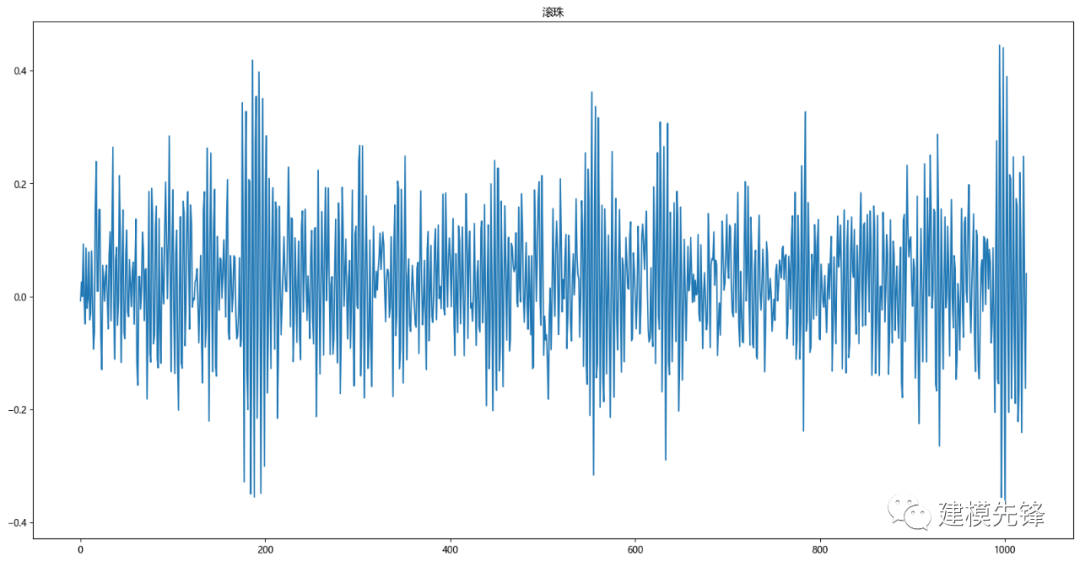
2.2.2 滚珠故障信号EMD分解
import numpy as np
import matplotlib.pyplot as plt
from PyEMD import EMD
t = np.linspace(0, 1, 1024)
data = np.array(data_list)
# 创建 EMD 对象
emd = EMD()
# 对信号进行经验模态分解
IMFs = emd(data)
# 绘制原始信号和每个本征模态函数(IMF)
plt.figure(figsize=(15,10))
plt.subplot(len(IMFs)+1, 1, 1)
plt.plot(t, data, 'r')
plt.title("Original signal", fontsize=10)
for num, imf in enumerate(IMFs):
plt.subplot(len(IMFs)+1, 1, num+2)
plt.plot(t, imf)
plt.title("IMF "+str(num+1), fontsize=10)
# 增加第一排图和第二排图之间的垂直间距
plt.subplots_adjust(hspace=0.4, wspace=0.2)
plt.show()
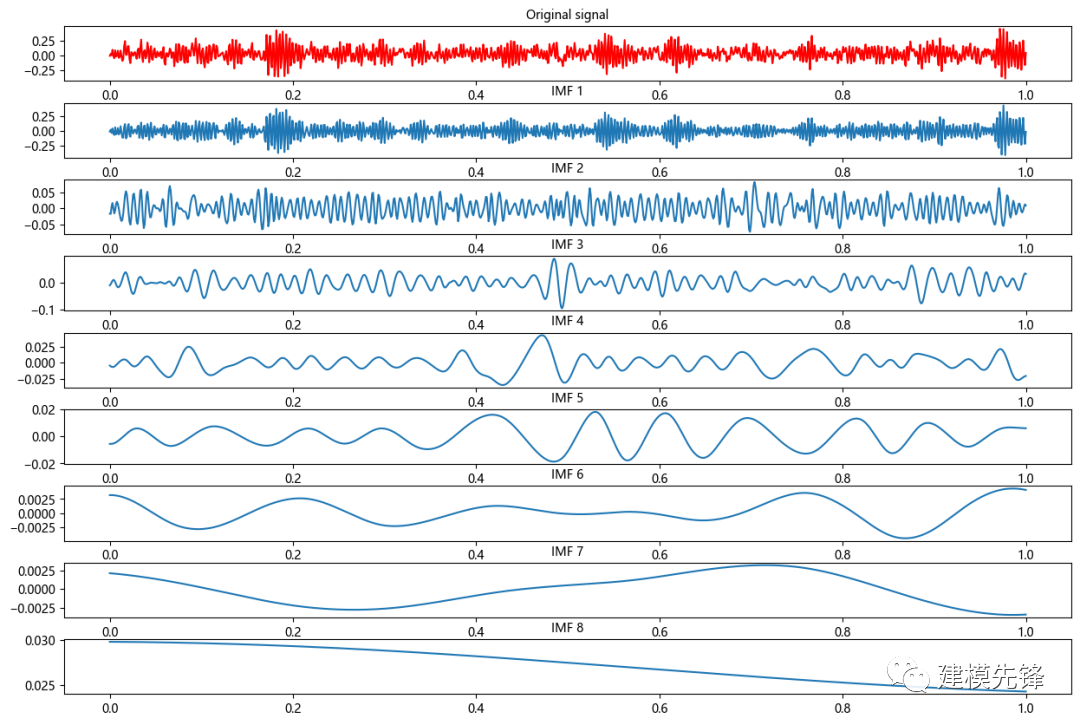
2.3 信号分量的处理
通过经验模态分解(EMD)得到了信号的分量,可以进行许多不同的分析和处理操作,以下是一些常见的对分量的利用方向:
(1)信号重构:将分解得到的各个本征模态函数(IMF)相加,可以重构原始信号。这可以用于验证分解的效果,或者用于信号的重建和恢复。
(2)去噪:对于复杂的信号,可能存在噪声或干扰成分。通过分析各个IMF的频率和振幅,可以识别和去除信号中的噪声成分。
(3)频率分析:分析每个IMF的频率成分,可以帮助理解信号在不同频率上的振荡特性,从而揭示信号的频域特征。
(4)特征提取:每个IMF代表了信号的局部特征和振荡模式,可以用于提取信号的特征,并进一步应用于机器学习或模式识别任务中。
(5)信号预测:通过对分解得到的各个IMF进行分析,可以探索信号的未来趋势和发展模式,从而用于信号的预测和预测建模。
(6)模式识别:分析每个IMF的时域和频域特征,可以帮助对信号进行模式识别和分类,用于识别信号中的不同模式和特征。
(7)异常检测:通过分析每个IMF的振幅和频率特征,可以用于探测信号中的异常或突发事件,从而用于异常检测和故障诊断。
在得到了信号的分量之后,可以根据具体的应用需求选择合适的分析和处理方法,以实现对信号的深入理解、特征提取和应用。对于后续的研究,主要利用IMF分类来对故障信号做模式识别,即故障分类。
-
Python轴承故障诊断—基于EMD-CNN的故障分类2023-12-12 3153
-
基于labview的轴承故障诊断与健康监测2024-03-18 5961
-
经验模态分解2015-12-02 4275
-
基于DSP+MCU的列车滚动轴承故障诊断系统研究2019-07-09 1813
-
电机轴承故障诊断与分析2021-09-01 1823
-
叶片的故障诊断和模态分析2008-12-13 961
-
滚动轴承故障诊断的实用技巧2010-10-29 1789
-
基于EMD和SVM的柴油机气阀故障诊断2011-07-27 947
-
基于EMD与Duffing振子的风机轴承早期故障诊断研究2017-01-02 840
-
基于CUDA加速的高速振动信号故障诊断方法2018-01-02 1194
-
轴承故障诊断方法2018-01-04 1016
-
PMSM局部退磁故障诊断2018-02-10 1018
-
基于变分模态分解优化的轴承故障诊断2021-06-01 874
-
基于经验模态分解等的齿轮故障诊断分析2021-06-22 835
-
模态分解合集matlab代码2024-12-20 1069
全部0条评论

快来发表一下你的评论吧 !

