

AI模型底层机制解析GPT与神经网络的关系
人工智能
描述
作者:京东云开发者-京东零售 欧阳舟俞
作为一名程序员,我们习惯于去了解所使用工具、中间件的底层原理,本文则旨在帮助大家了解 AI 模型的底层机制,让大家在学习或应用各种大模型时更加得心应手,更加适合没有 AI 基础的小伙伴们。
一、GPT 与神经网络的关系
GPT 想必大家已经耳熟能详,当我们与它进行对话时,通常只需关注自己问出的问题(输入)以及 GPT 给出的答案(输出),对于输出内容是如何产生的,我们一无所知,它就像一个神秘的黑盒子。

GPT 是一种基于神经网络的自然语言处理(NLP)模型,使用大量数据输入神经网络对模型进行训练,直到模型的输出在一定程度上符合我们的预期,训练成熟的模型就可以接收用户的输入,并针对输入中的关键信息给出经过 “思考” 后的答案。想要弄明白 GPT 究竟是如何 “思考” 的,或许我们可以从神经网络出发。
二、什么是神经网络
那么,神经网络到底是什么呢?或者说,为什么是神经网络? 高中的生物学告诉我们,人类的神经系统由数以亿计的神经元连接而成,它们是生物学上的细胞,有细胞体、树突、轴突等主要结构,不同神经元之间的树突与轴突通过突触与其他神经元相互连接,形成复杂的人脑神经网络。
人工智能为了使机器获得接近人类的智力,尝试效仿人脑的思考过程,创造出了一种模仿人脑神经元之间相互连接的计算模型 —— 神经网络。它由多层神经元组成,每个神经元接收输入并产生相应的输出。根据上述定义,图 1 中黑盒子的内部结构已初具轮廓,下图中的每个圆圈都代表一个神经元,神经元具有计算能力,可以将计算出来的结果传递到下一个神经元。
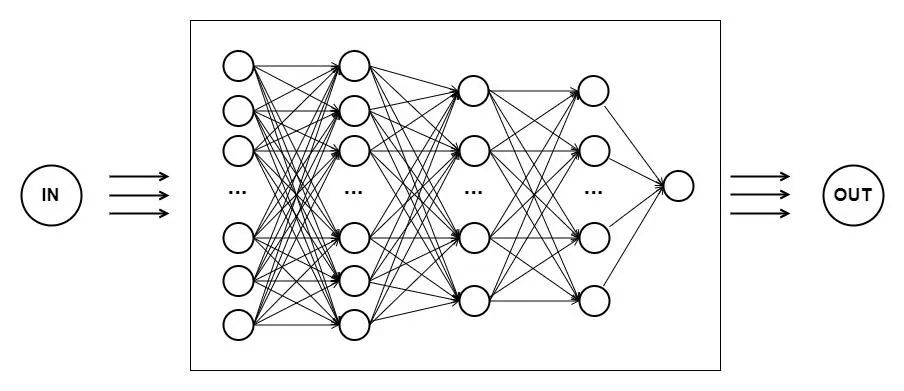
在生物学中,大脑的结构越简单,智力也就越低;相应地,神经系统越复杂,能处理的问题越多,智力也就越高。人工神经网络也是如此,越复杂的网络结构计算能力越强大,这也是为什么发展出了深度神经网络。之所以被称为 "深度",是因为它具有多个隐藏层(即上图中纵向神经元的层数),相对于传统的浅层神经网络,深度神经网络具有更多的层级结构。 训练深度神经网络的过程就叫做深度学习。构建好深度神经网络之后,我们只需要将训练数据输入到神经网络中,它就会自发地学习数据中的特征。比如说我们想要训练一个深度神经网络来识别猫,只需要将大量不同种类、不同姿势、不同外观的猫的图片输入到神经网络中让它学习。训练成功后,我们将一张任意的图片输入到神经网络中,它会告诉我们里面是否有猫。
三、神经网络是如何计算的
现在,我们已经知道了什么是神经网络以及它的基本结构,那么神经网络中的神经元是如何对输入数据进行计算的呢? 在此之前,我们要解决一个问题:数据是如何输入到神经网络中的?下面以图像和文本类型的数据为例讲解。
数据是如何输入到神经网络中的
1、图像输入处理
想象一个画面:当我们把一张图片放大到一定程度时,可以看到一格一格的小方块。这个小方块就称为像素点,一张图片的像素点越多,说明像素越高,图片越清晰。每个像素点仅由一种颜色构成,光学中的三原色包含红色、绿色、蓝色,通过不同程度地混合这三种颜色可以产生出所有其他颜色。在 RGB 模型中,每种颜色的强度可以用一个数值来表示,通常在 0 到 255 之间。红色的强度值为 0 表示没有红色光,255 表示最大强度的红色光;绿色和蓝色的强度值也是类似的。 为了存储一张图像,计算机要存储三个独立的矩阵,这三个矩阵分别与图像的红色、绿色和蓝色的强度相对应。如果图像的大小是 256 * 256 个像素,那么在计算机中使用三个 256 * 256 的矩阵(二维数组)就能表示这张图像。可以想象将三个矩阵表示的颜色重叠堆放在一起,便可显现出图像的原始样貌。 现在我们得到了图像在计算机中的表示方式,那么如何将它输入到神经网络呢? 通常我们会把上述三个矩阵转化为一个向量,向量可以理解成 1 * n(行向量)或 n * 1(列向量)的数组。那么这个向量的总维数就是 256 * 256 * 3,结果是 196608。在人工智能领域中,每一个输入到神经网络的数据都被叫做一个特征,那么上面的这张图像中就有 196608 个特征。这个 196608 维的向量也被叫做特征向量。神经网络接收这个特征向量作为输入,并进行预测,然后给出相应的结果。
2、文本输入处理
文本是由一系列字符组成的,首先需要将文本划分成有意义的单词,这个过程称为分词。在分词后,构建一个由出现的所有单词或部分高频单词组成的词汇表(也可以使用已有的词汇表)。词汇表中的每个单词都会被分配一个唯一索引,这样可以将文本转换为离散的符号序列,方便神经网络进行处理。在输入神经网络之前,通常会将文本的符号序列转换为密集的向量表示。 以文本 “How does neural network works?” 为例:
分词:["how", "does", "neural", "network", "works"]
构建词汇表:{"how": 0, "does": 1, "neural": 2, "network": 3, "works": 4}
序列化文本数据:["how", "does", "neural", "network", "works"] -->[0, 1, 2, 3, 4]
向量化:
#此处以one-hot向量表示法为例: [[1, 0, 0, 0, 0] [0, 1, 0, 0, 0] [0, 0, 1, 0, 0] [0, 0, 0, 1, 0] [0, 0, 0, 0, 1]]最后,将向量序列作为输入,给神经网络进行训练或预测。 至此我们已经知道了数据以怎样的形式输入到神经网络中,那么神经网络是如何根据这些数据进行训练的呢?
神经网络是如何进行预测的
首先明确模型训练和预测的区别:训练是指通过使用已知的数据集来调整模型的参数,使其能够学习到输入和输出之间的关系;预测是指使用训练好的模型来对新的输入数据进行预测。 神经网络的预测其实是基于一个很简单的线性变换公式: 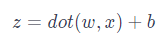 其中,x表示特征向量,w是特征向量的权重,表示每个输入特征的重要程度,b表示阈值,用于影响预测结果。公式中的 dot () 函数表示将 w和 x进行向量相乘。举例:如果一个输入数据有 i个特征,代入公式计算结果为:
其中,x表示特征向量,w是特征向量的权重,表示每个输入特征的重要程度,b表示阈值,用于影响预测结果。公式中的 dot () 函数表示将 w和 x进行向量相乘。举例:如果一个输入数据有 i个特征,代入公式计算结果为: 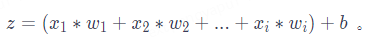
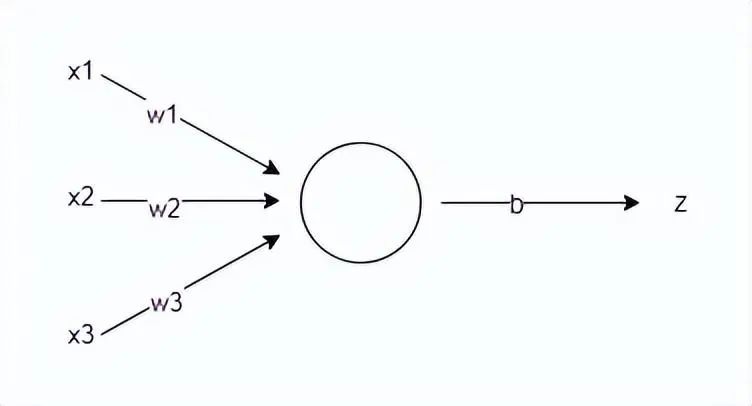
如何理解这个公式呢?假设你需要决策周末是否去公园划船,你对此犹豫不决,需要神经网络帮你做决定。决定是否去划船有三个因素:天气是否晴朗温暖、地点是否远近适中、同行玩伴是否合心意。实际情况是出行那天天气为阴且偶有阵风、地点在 20km 外的偏远郊区、同行玩伴是心仪已久的大帅哥。这三个因素即为输入数据的特征向量 x=[x1, x2, x3],我们需要根据特征对结果的影响来设置特征值,如 “天气不好” 和 “地点偏远” 对结果具有负向的影响,我们可以把它设为 - 1,“同行玩伴是心仪已久的大帅哥” 显然对结果有大大的正向影响,可以把它设为 1,即特征向量 x=[-1, -1, 1]。接下来,需要根据你的偏好来设置三个特征的权重,也就是每个因素对你最终决策的影响程度。如果你不在乎天气和地点,只要与大帅哥同行便风雨无阻,那么可以将权重设置为 w=[1, 1, 5];如果你是个懒狗,那你可能会设置权重为 w=[2, 6, 3];总之,权重是根据对应特征的重要程度来确定的。 我们选择第一组权重 w=[1, 1, 5],特征向量为 x=[-1, -1, 1], 并设置阈值 b=1,假设结果 z ≥ 0 表示去,z < 0 表示不去,计算预测结果 z = (x1*w1 + x2*w2 + x3*w3) + b = 4 > 0,因此神经网络给出的预测结果是:去公园划船。 上面使用的公式 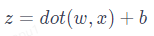 本质上是一种逻辑回归,用于将输入数据映射到二分类的概率输出。逻辑回归通常使用一个特定的激活函数来实现将 z值到 [0, 1] 的映射关系,即 Sigmoid 函数,它将线性变换的结果通过非线性映射转化为概率值。通常,大于等于 0.5 的概率值被视为正类,小于 0.5 的概率值被视为负类。 Sigmoid 函数的公式和图像如下所示:
本质上是一种逻辑回归,用于将输入数据映射到二分类的概率输出。逻辑回归通常使用一个特定的激活函数来实现将 z值到 [0, 1] 的映射关系,即 Sigmoid 函数,它将线性变换的结果通过非线性映射转化为概率值。通常,大于等于 0.5 的概率值被视为正类,小于 0.5 的概率值被视为负类。 Sigmoid 函数的公式和图像如下所示: 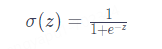
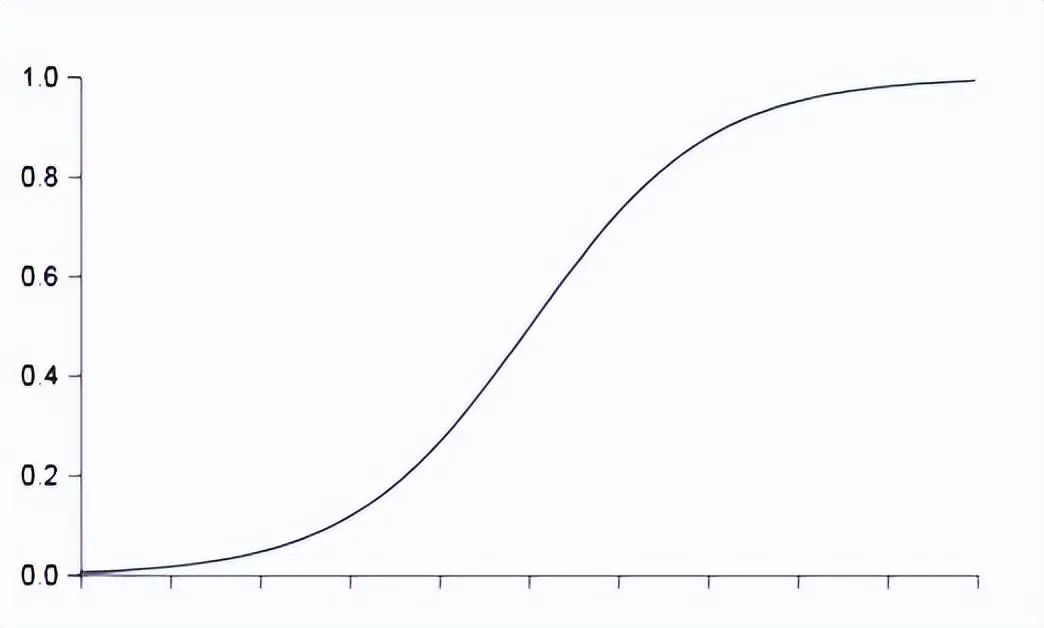
除了能将结果输出范围控制在 0 到 1 之间,Sigmoid 函数(或其他激活函数)另外一个重要作用就是将线性变换的结果进行非线性映射,使神经网络可以学习和表示更加复杂的非线性关系。如果没有激活函数,神经网络只能解决简单的线性问题;加入激活函数之后,只要层数足够多,神经网络就能解决所有问题,因此激活函数是必不可少的。
神经网络是如何进行学习的
得到预测结果后,神经网络会通过损失函数判断预测结果是否准确,如果不够准确,神经网络会进行自我调整,这就是学习的过程。 损失函数用于衡量模型的预测结果与真实标签之间的误差。通过将预测值与真实值进行比较,损失函数提供了一个数值指标,反映了模型当前的预测性能。较小的损失值表示模型的预测结果与真实标签更接近,而较大的损失值表示预测误差较大。下面介绍一个常用于二分类问题的损失函数(对数损失):
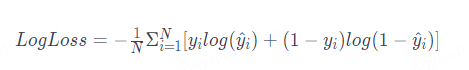

神经网络学习的目的,就是通过调整模型的参数使损失函数达到最小值,从而改善模型的预测性能,这个过程也称为模型的训练。梯度下降算法可以解决这一问题,通过该算法找到合适的 w(特征的权重)和 b(阈值),梯度下降算法会一步一步地改变 w 和 b的值,使损失函数的结果越来越小,也就是使预测结果更精准。

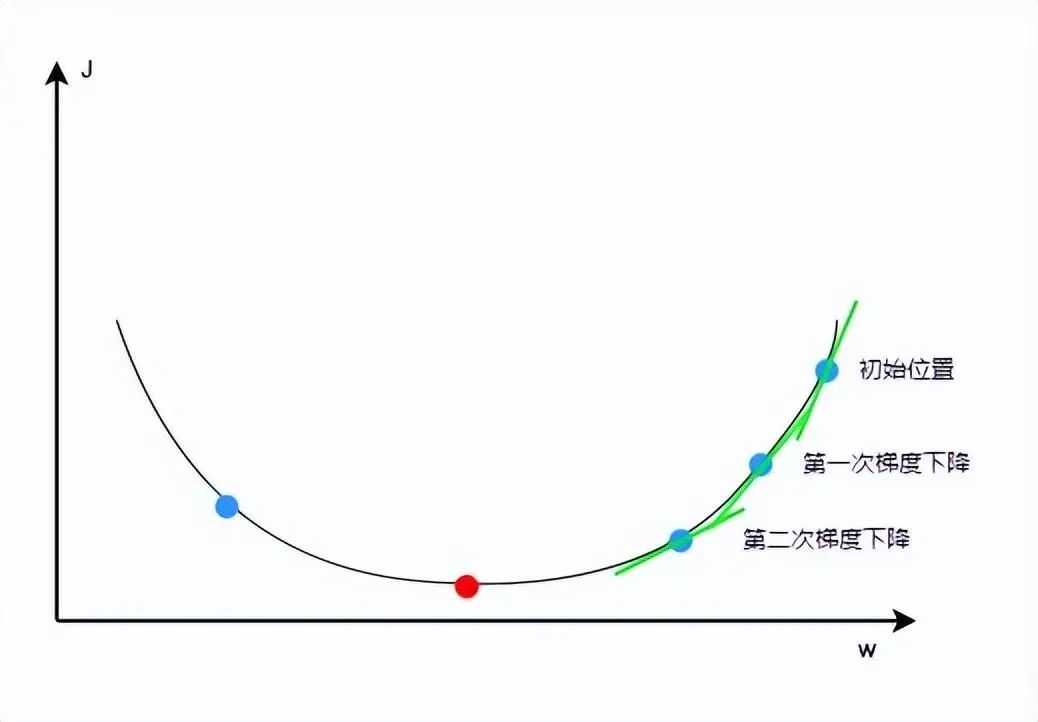
这里需要注意的是,如果学习率设置过小,则需要多次梯度下降才能到达最低点,浪费机器运行资源;如果设置过大,则可能错过最低点直接到了图中左侧的点位,因此需要根据实际情况选择一个正确的学习率。 神经网络的计算过程主要有两个步骤:正向传播和反向传播。正向传播用于计算神经元的输出,也就是上述对输入特征进行加权求和、并通过激活函数进行非线性变换的过程;反向传播用于更新优化模型参数,通过计算损失函数关于模型参数的梯度,从输出层向输入层反向传播梯度的过程(反向传播涉及大量的数学计算,感兴趣的读者可以深入了解)。
四、综述
综上所述,神经网络训练和学习的过程其实就是对模型参数进行不断调优、减少预测损失值过程。经过充分训练后,模型能够从输入数据中学习到有效的特征表示和权重分配,从而能够对未见过的数据进行准确的预测。训练完成的神经网络模型可以应用于各种实际问题。比如,在图像分类任务中,卷积神经网络可以根据输入图像的特征自动识别物体或图案;在自然语言处理任务中,循环神经网络可以理解和生成文本;在推荐系统中,多层感知机神经网络可以根据用户的历史行为进行个性化推荐。 这篇文章对神经网络的工作机制做了浅层次的讲解,如有不正之处,敬请指教!
审核编辑:黄飞
-
PyTorch神经网络模型构建过程2024-07-10 1343
-
神经网络模型的原理、类型及应用领域2024-07-02 2672
-
神经网络是如何学习预测的?2023-12-27 1106
-
什么是神经网络?神经网络是如何工作的?GPT与神经网络的关系2023-12-13 2579
-
cnn卷积神经网络模型 卷积神经网络预测模型 生成卷积神经网络模型2023-08-21 1922
-
卷积神经网络模型发展及应用2022-08-02 13207
-
轻量化神经网络的相关资料下载2021-12-14 2032
-
嵌入式Linux平台部署AI神经网络模型Inference的方案2021-11-02 734
-
如何使用stm32cube.ai部署神经网络?2021-10-11 4533
-
在STM32上验证神经网络模型2021-08-03 1800
-
如何构建神经网络?2021-07-12 1862
-
【AI学习】第3篇--人工神经网络2020-11-05 4120
-
神经网络教程(李亚非)2012-03-20 56651
全部0条评论

快来发表一下你的评论吧 !

