

pipeline ADC的实现原理及基本结构(2)
描述
在之前的笔记中我简要记录了pipelined ADC中的数字校准技术,也就是消除子ADC失调的方法,但记录的并不全面,理解的也不够透彻,这里重新系统地再解释一下其原理及由来。
本文主要参考了Imran Ahmed的”Pipelined ADC Design and Enhancement Techniques”一书
Imran Ahmed的书中提供了一个很好的角度来理解流水线ADC的工作原理,我们可以使用除法来进行类比,回忆我们计算十进制除法时的过程,首先,将被除数与除数进行比较,找到一个数使得其与除数的乘积最接近而不超过被除数,将其作为最高位的商,之后将被除数减去除数和此位商的乘积,得到的结果乘以10,继续重复上述步骤。
根据以上的描述结果可以很清晰地看到,除法中每位商的计算过程与1bit的流水线子级的运算过程非常相似,被除数是要量化的模拟量,除数是LSB,商就是转化结果,10就是级间增益,每次新得到的被除数就是残差。
那么继续思考这个过程,如果某一位商的运算结果错了怎么办,注意这个情况就对应于pipelined ADC某个子级中比较器的判决电压产生偏移导致了误码,举个例子,50/7,正常情况下的计算流程如下
| 位数 | 当前位商(当前子级的输出) | 当前位商*除数(子DAC转换结果) | 余数(残差) | 新的被除数(放大到满量程的残差) |
| 1 | 7 | 49 | 1 | 10 |
| 2 | 1 | 7 | 3 | 30 |
| 3 | 4 | 28 | 2 | 20 |
| 4 | 2 | 14 | 6 | 60 |
| 5 | 8 | 56 | 4 | 40 |
| 6 | 5 | 35 | 5 | 50 |
根据上表,正常计算得到的结果为7.14285余5。
接下来假设第四位的商计算错误(对应于第四级流水线子级的比较器失调),将正确的2变为3,计算流程如下。
| 位数 | 当前位商(当前子级的输出) | 当前位商*除数(子DAC转换结果) | 余数(残差) | 新的被除数(放大到满量程的残差) |
| 1 | 7 | 49 | 1 | 10 |
| 2 | 1 | 7 | 3 | 30 |
| 3 | 4 | 28 | 2 | 20 |
| 4 | 3 | 21 | -1 | -10 |
| 5 | -2 | -14 | 4 | 40 |
| 6 | 5 | 35 | 5 | 50 |
得到的结果为7.143(-2)5余5,很明显,验证后这个结果也是正确的。
那么就可以得到结论,即使某位发生了误码,只要将错误的结果完整地继续传递下去,此运算结构依旧可以得到正确的结果。但是需要注意的是上述结论存在一个非常重要的前提,必须要将错误的结果完整地传递下去。
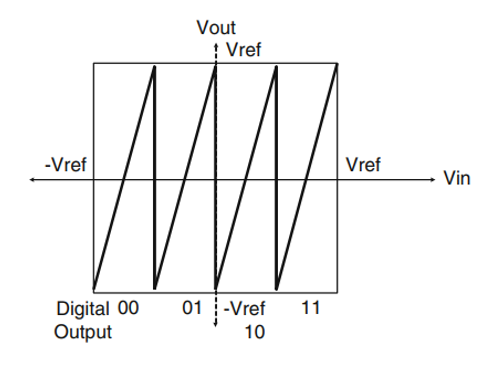
考虑一个两位子级的传输特性曲线,如上图所示,我们可以发现,输出电压最大值和最小值已经到达了Vref,一旦判决电压发生偏移,如下图所示,就会导致输出超出下级的量程,换句话说,下一级并没有足够的位数来将超出量程的电压记录下来,那么之前得出的结论也就不再适用了。
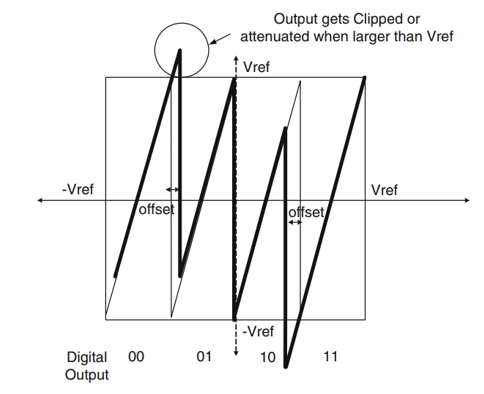
那么应该如何进行改进呢,很明显,既然下一级的量程不够,我们可以将当前级的级间增益缩小,如下图所示,将级间增益由4缩小为2(注意这里实际上是将有效位减小为1位了),这样一来,当前级的输出就只有-Vref/2~ Vref/2的范围了,而下一级的输入范围为-Vref~ Vref,正负两端都留有Vref/2的余量,对应于比较器的判决电压有Vref/4的偏移余量,换句话说,只要比较器判决电压的偏移在正负Vref/4的范围内,错误信息都可以完整地传输到下一级。
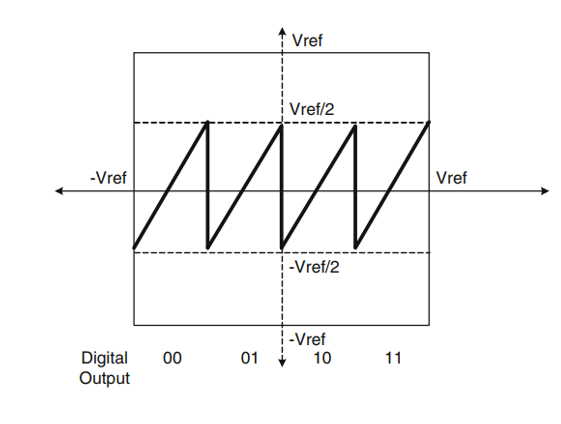
对于级间增益减半后的计算过程,从数字的角度来理解比较容易。举个例子,假设理想的输出数字量为4’b1011,转换所用的ADC由一个级间增益减半的2-bit子级和一个3-bit Flash ADC构成,模拟输入进第一级后输出数字量为4’b10zz(这里用数码z表示0的权重,注意这里数码0的权重是负的),相减得到的残差用数字量来表示为4’bzz11,由于级间增益减半,有效位只有一位,只需要左移一位得到4’bz11z,那么Flash ADC的转换结果也就是3’bz11,等价转化一下就是3’b101,将这个结果的最高位与2-bit子级的低位对齐进行错位相加得到结果为4’b1011,正好为理想的输出量。
观察上述错位相加的过程,由于数码0的权重是负的,这就导致不能用简单的二进制加法进行运算,注意到这里0+1=z,这相当于在数字逻辑中引入了减法运算,这是十分麻烦的,我们期望即便是在这样的权重分配下依旧可以使用最简单的二进制加法进行错位相加。(Imran Ahmed的书中只是简单提了一句,引文Chien, G.: High-speed, lower-power, low-voltage pipelined analog-to-digital converter. Masters of Science thesis, University of California Berkeley (1996),但我并未找到这篇文献,有兄弟有资源的可以分享一下,以下都是我的个人理解)
那么应该如何实现呢,首先我们罗列出所有错位相加的可能,如下表所示,假设有两个级间增益减半的2-bit的子级级联,其中第一行为第一级的输出结果,第二行为第二级的输出结果,结果1为直接使用普通二进制加法错位相加得到的输出,结果2位为正确的相加结果。
| 第一级 | 00 | 01 | 10 | 11 | ||||
| 第二级 | 01 | 10 | 01 | 10 | 01 | 10 | 01 | 10 |
| 结果1 | 001 | 010 | 011 | 100 | 101 | 110 | 111 | 1000 |
| 结果2 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
可以明显看出,结果1仅仅与结果2相差1,也就是说,如果将第二级的输出结果减去1,那么直接采用普通二进制加法错位相加得到的总的输出结果就是正确的。举个例子,第二级输出为01,那么只要将01变为00即可,但这里需要注意,由1变到z对应于减Vref/8,而由1变到0对应于减Vref/4。
那么最简单的方法,直接将转移特性曲线向下平移Vref/2,也就是将输出给下一级的残差减小Vref/2(这是级间放大后的结果,从放大前角度看就是Vref/4),通过上述分析,这么做就可以直接对输出进行错位相加了。
然而新的问题又出现了,注意到直接将转移特性曲线向下平移后输出最小值又到达下限-Vref,这样的一来比较器的判决电压一旦发生负的偏移输出又会超下一级的量程,我们之前将级间增益减半的做法又失去了作用。然而我们还可以发现,正的余量增加到了原来的2倍,既然如此,我们不妨将比较器所有阈值电压都正向偏移Vref/4,这样一来正负两端的余量就又都是Vref/4了。最后得到的转移特性曲线如下图所示。注意这里阈值电压的偏移不会引起任何输出上的错误,就像之前说的,错误的量被完整地传递下去了。
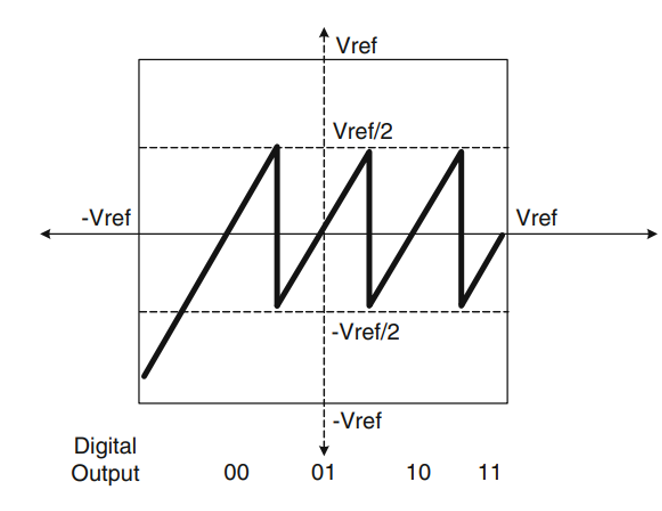
同样,我们举例具体描述一下转换过程,假设理想结果为4’b1011,ADC由一个级间增益减半并将比较器阈值右移Vref/4的2-bit子级和一个3-bit Flash ADC构成,模拟输入大小为Vref/2- Vref/4+ Vref/8+ Vref/16 = 7Vref/16,对应于区间10,输出数字码10,而由于阈值电压右移Vref/4,子DAC输出的模拟量为Vref/2- Vref/4+ Vref/4 = Vref/2,残差为2*(7Vref/16 - Vref/2) = - Vref/8,同样可以用数字量来表示,子DAC的输出为4’b10zz + 4’bz1zz(加Vref/4) = 4’b1zzz,计算残差,4’b1011 – 4’b1zzz = 4’bz011,左移一位得到4’b011z,经3-bit Flash ADC转换出的结果为3’b011,直接使用普通二进制加法进行错位相加,得到4’b1011。结果是正确的。
我们继续观察现在的传输特性曲线,注意到“11”这个区间实际上进行了一次多余的转折判断,实际上低位1的判断完全可以交给下一级进行,纵轴上还存在Vref/2~Vref的余量,也就是说这个比较器的存在是可有可无的,那么再加入它就产生浪费了,因此我们将其移除。注意移除后正确性是可以保障的,因为当前级未量化的模拟输出会继续送往下级进行量化。得到的传输特性曲线如下图所示。
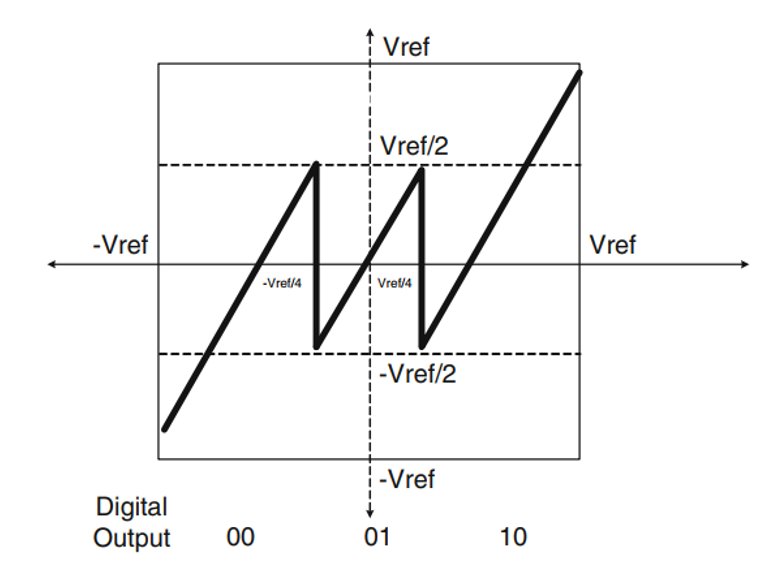
这个曲线就是非常经典的1.5-bit的单级结构了。前面我已经详细介绍了它的由来,接下来我从另一个角度对其进行解释。
一种更加简单的理解方式就是认为接近转折电压0处的模拟输入量非常容易由于比较器判决电压的偏移而导致误码和失码现象。因此在这附近单独划分一个区间,在当前级不进行判断,对应于MDAC开关接到0电平(这里01对应于-Vref/2+Vref/4=Vref/4,由于曲线整体下移了Vref/4,因此接到0),也就是将模拟输入原封不动放大后直接传给下一级,由下一级进行判断。
这种理解方式也可以认为是正确的,但解释并不透彻,也并未说明可以直接进行普通二进制错位相加的原理,因此要想深刻地理解此技术的原理应该去了解它的由来及演变过程。
审核编辑:黄飞
-
从技术到产品 | 士模Pipeline ADC2025-04-28 1194
-
浅析SpinalHDL中Pipeline中的复位定制2024-03-17 1714
-
什么是pipeline?Go中构建流数据pipeline的技术2024-03-11 1589
-
pipeline ADC的实现原理及基本结构(1)2023-12-14 4645
-
Pipeline中throwIt的用法2023-10-21 1163
-
国产ADC芯片——adc芯片的多种结构2023-10-09 3611
-
核芯互联最新推出一款 Pipeline结构的模数转换器(ADC)2023-09-04 2612
-
SpinalHDL里pipeline的设计思路2023-08-16 1543
-
pipeline_a2dp_sink_stream蓝牙卡顿怎么解决?2023-03-10 573
-
pipeline ADC的实现原理及基本结构笔记分享2022-09-15 3074
-
修改V4L2的Video Pipeline的devicetree2022-08-02 2587
-
基于Ginkgo 2的ADC实现虚拟示波器功能2019-02-21 1339
-
14位Pipeline ADC设计的带隙电压基准源技术2010-04-23 3985
-
Pipeline ADCs Come of Age2009-04-16 1324
全部0条评论

快来发表一下你的评论吧 !

