梯形图编程原则与PLC程序设计方法

梯形图程序设计

梯形图编程原则与 PLC 程序设计方法

（1） 输入 / 输出继电器、内部辅助继电器、定时器、计数器等器件的触点可以多次重复使 用，无需复杂的程序结构来减少触点的使用次数。

（2） 梯形图每一行都是从左母线开始，线圈终止于右母线。触点不能放在线圈的右边，如下图所示

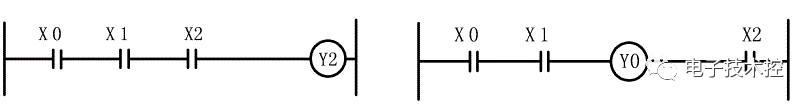
正确的电路 错误的电路

（3） 除步进程序外，任何线圈、定时器、计数器、高级指令等不能直接与左母线相连。

（4） 在程序中，不允许同一编号的线圈两次输出（双线圈输出）。下面的梯形图是不允许的。

（5） 不允许出现桥式电路。

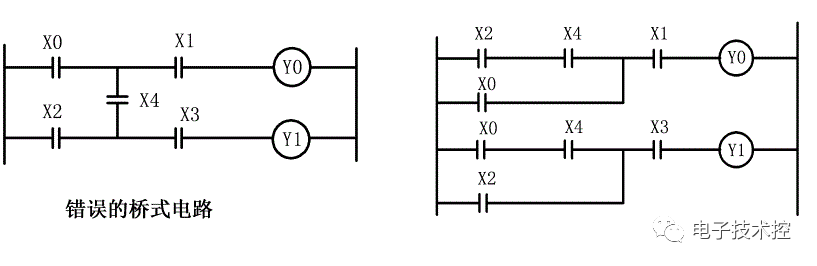
（6） 程序的编写顺序应按自上而下、从左至右的方式编写。为了减少程序的执行步数，程序应为左大右小，上大下小。如：

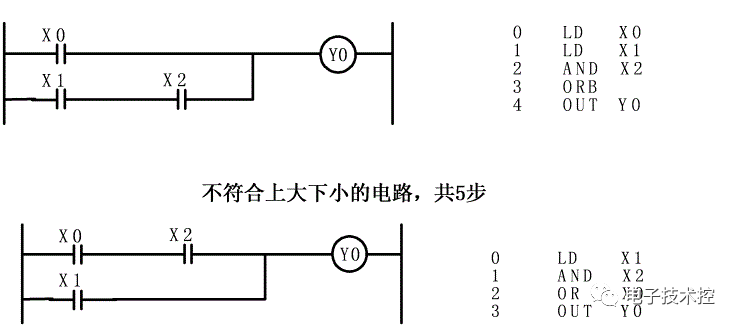
符合上大下小的电路，共 4 步

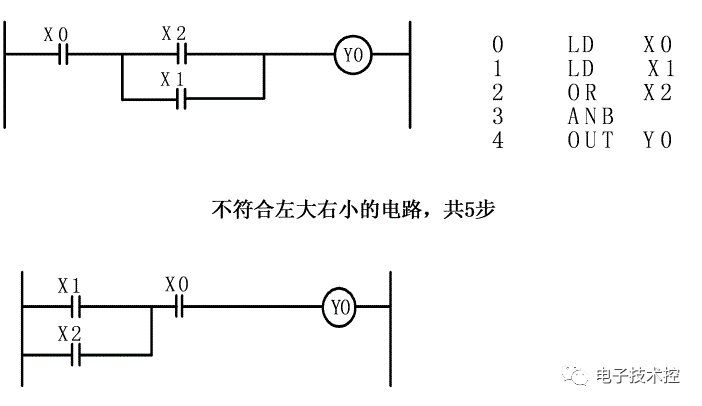
符 合左大右小的电路，共 4 步

（7） 输入设备尽可能用常开触点

（8） PLC 程序设计常用的经验设计法

在传统继电器－接触器控制图和 PLC 典型控制电路的基础上，依据积累的经验进行翻译、修改和完善，得到最终的控制程序。

（9） 常用的 PLC 典型控制电路

梯形图程序设计的常用方法 —— 逻辑法。

逻辑法：就是应用逻辑代数以逻辑组合的方法和形式设计程序。逻辑法的理论基础是逻辑函数，逻辑函数就是逻辑运算与、或、非的逻辑组合。因此，从本质上来说， PLC 梯形图程序就是与、或、非的逻辑组合，也可以用逻辑函数表达式来表示。

（1） 基本方法：用逻辑法设计梯形图，必须在逻辑函数表达式与梯形图之间 建立一种一一对应关系，即梯形图中常开触点用原变量（元件）表示，常闭触点用反变量（元件上加一小横线）表示。触点（变量）和线圈（函数）只有两个取值“ 1 ” 与“ 0 ” ， 1 表示触点接通或线圈有电， 0 表示触点断开或线圈无电。触点串联用逻辑“与”表示，触点并联用逻辑“或”表示，其他 复杂的触点组合可用组合逻辑表示，他们的对应关系如下表所示。

逻辑函数表达式	梯形图	逻辑函数表达式	梯形图
逻辑“与” M0=X1.X2		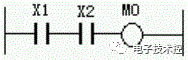“与”运算式 M0=X1.X2---Xn
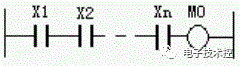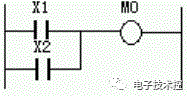
逻辑“或” M0=X1+X2		“或 / 与”运算式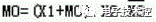
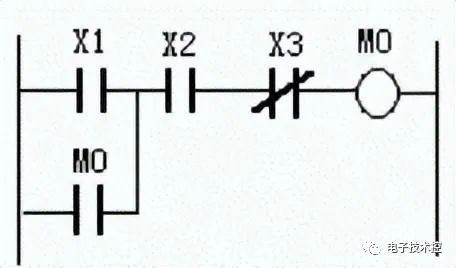逻辑“非”	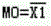	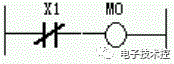“与 / 或”运算式 M0=(X1.X2)+(X3.X4)

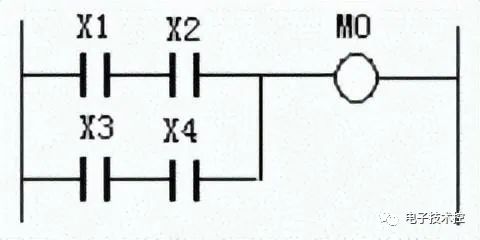（2） 设计步骤：

1） 通过分析控制要求，明确控制任务和控制内容；

2） 确定 PLC 的软元件（输入信号、输出信号、辅助继电器 M 和定时器 T ），画出 PLC 的外部接线图；

3） 将控制任务、要求转换为逻辑函数（线圈）和逻辑变量（触点），分析触点与线圈的逻辑关系，列出真值表；

4） 写出逻辑函数表达式；

5） 根据逻辑函数表达式画出梯形图；

6） 优化梯形图

（3） 逻辑法的应用

用逻辑法设计三相异步电动机 Y/ △降压起动控制的梯形图。

1） 明确控制任务和控制内容

按下起动按钮 SB1 ，时间继电器 KT 和起动用接触器 KMY 线圈得电，之后主接触器 KM 线圈得电并自锁，进行 Y 形起动。当 KT 的延时到达， KMY 线圈失电，同时 KM △线圈得电，电动机完成 Y 形起动，进入△形正常运行。在此过程中，按下停止按钮 SB 或热继电器 FR 动作，电动机无条件停止。

2） 确定 PLC 的软元件，画出 PLC 的外部接线图

PLC 的输入信号：起动按钮 SB1(X1) ，停止按钮 SB(X0) ，热继电器常开触点 FR(X2) 。PLC 的输出信号：主接触器 KM(Y0) ，起动接触器 KMY(Y1) ，运行接触器 KM △ (Y2) 。定时器 (T0) 。根据上述 I/O 信号，可画出 PLC 的外部接线图，如图 5 所示。

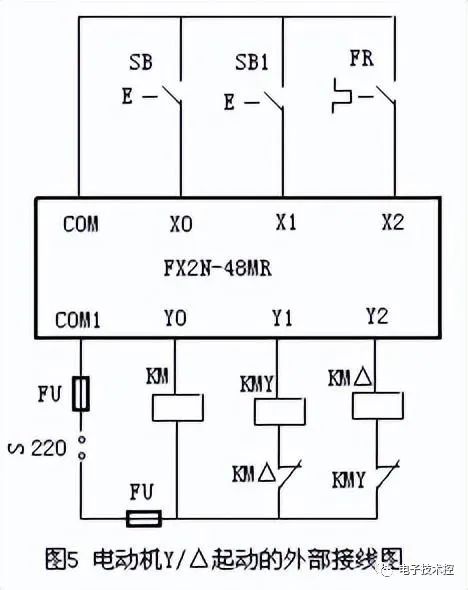
3） 列出真值表

真值表就是根据控制要求，列出的线圈函数和触点变量的取值，即当线圈函数为 1 时，必须使哪些触点变量为 1 ，当线圈函数为 0 时，必须使哪些触点变量为 0 。例如，当起动用接触器为 1 时，就必须使起动按钮为 1 或起动接触器为 1 ；当起动用接触器为 0 时，就必须使停止按钮或热继电器或运行或定时器为 0 。根据控制要求，可列出其真值表，如图 6 所示。

触点	线圈
X0	X1	X2	Y0	Y1	Y2	T0	Y1	Y0	Y2	T0
	1			1			1
0		0			0	0	0
			1	1				1
0		0						0
					1	1			1
0		0		0					0
	1				0	1				1
0		0								0

图 6 电动机 Y/ △降压起动真值表

4） 列出逻辑函数表达式

将真值表中线圈函数为 1 的触点变量的逻辑式与上线圈函数为 0 的各触点变量的反变量，即为线圈函数的逻辑表达式，因此，可列出如下的逻辑函数表达式：

5） 画出梯形图

根据上述逻辑函数表达式以及逻辑函数表达式与梯形图的对应关系，可画出图 7 所示的梯形图。

　　审核编辑：汤梓红