一种电容加载腔体带通滤波器的设计方案

利用电容加载传输线缩短理论，重新设计腔体滤波器的内部结构，利用T型梳状结构实现加载电容，减小腔体尺寸。仿真设计并实际加工出一个中心频率为2.4GHz的带通滤波器。在保持普通腔体滤波器高功率容量、小差损、高带外抑制等优点的基础上有效减小滤波器体积，从而有利于其小型化应用。

滤波器作为一类重要的微波无源器件广泛应用在现代通信系统、雷达系统和电子对抗系统中。其性能往往对整个系统造成重大影响。随着现代通信技术的不断发展，频谱资源的日益枯竭而导致各微波通信系统频率分布间隔不断密集。由于这些原因使得对滤波器性能要求越来越高。同时由于星载、机载微波系统对对滤波器的功率容量、插损、带外抑制、重量、体积有特殊要求，使得滤波器要在提高性能的同时小型化方向发展。

1 电容加载传输线缩短理论

图1（a）中给出了一个特性阻抗为Z，长度为 L的传输线，其[A]矩阵如下：

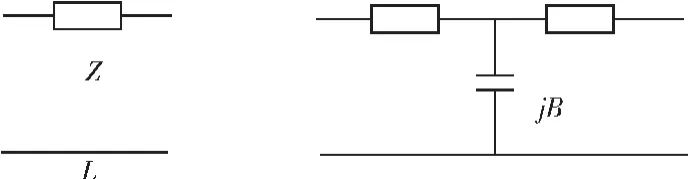
图1 传输线与加载电容的传输线
Fig.1 Transmission line and the transmission line of the loading capacity

图1（b）中为电容加载的传输线模型。两段传输线的特性阻抗都为Z0，长度为l0。两段传输线中间并联电容的电抗为jB。该网络的[A]矩阵用[B]表示，其表达式如下：

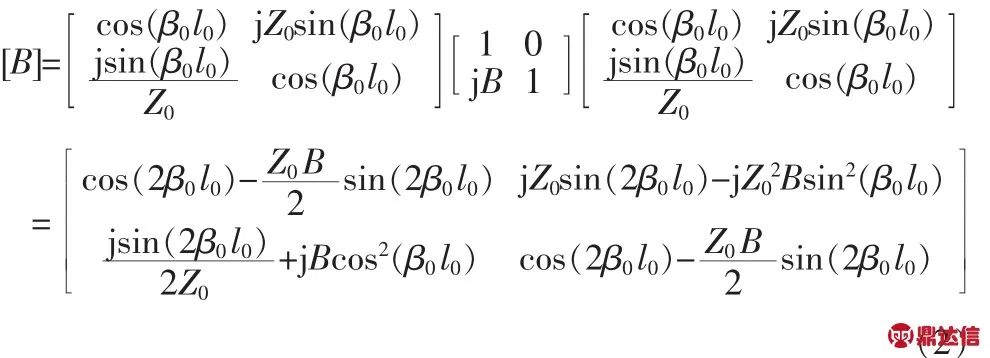
对两电路进行等效，当 β=β0，[A]=[B]时，由式（1），（2）可得：

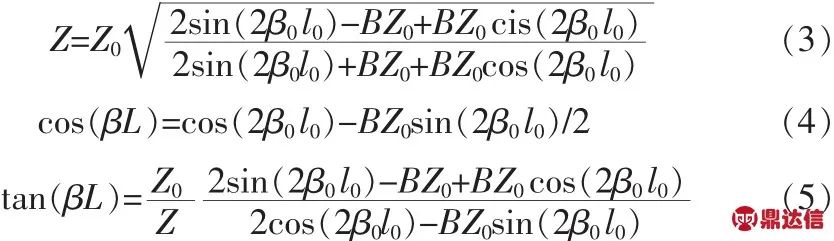
从式（3）中可以看出：Z≥Z0；从式（4），（5）中可以看出：当

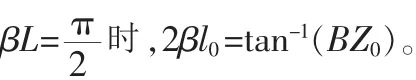
若 BZ0很大时，2βl0将会变得很小。也就是说，电容加载传输线的长度将大大缩短。

若滤波器采用空腔谐振器作为基本谐振单元，利用λg/2作为谐振腔长度，由上述理论分析可知，将并联电容加载在半波长空腔谐振器中，可以在谐振频率不变的情况下减小腔体谐振器尺寸。可通过以下两种方法实现谐振腔的电容加载。1）在谐振腔中加入一段金属凸台，其结构示意图如图2（a）所示。 金属凸台的长度、宽度和高度分别为 Ls1、Ws1、Hs1，其等效电路如图1右部所示，金属凸台等效为电路中的并联电容；2）在谐振腔中加入一段T型金属结构，其结构示意图如图2（b）所示。T型结构下端金属长方体的长度、宽度、高度分别为Ls2、Ws2、Hs2，T型结构 上端金属长方体的长度、 宽度、高度分别为 Ls3、Ws3、Hs3，其等效电路如图 1右部所示，T型金属结构等效为电路中的并联电容。

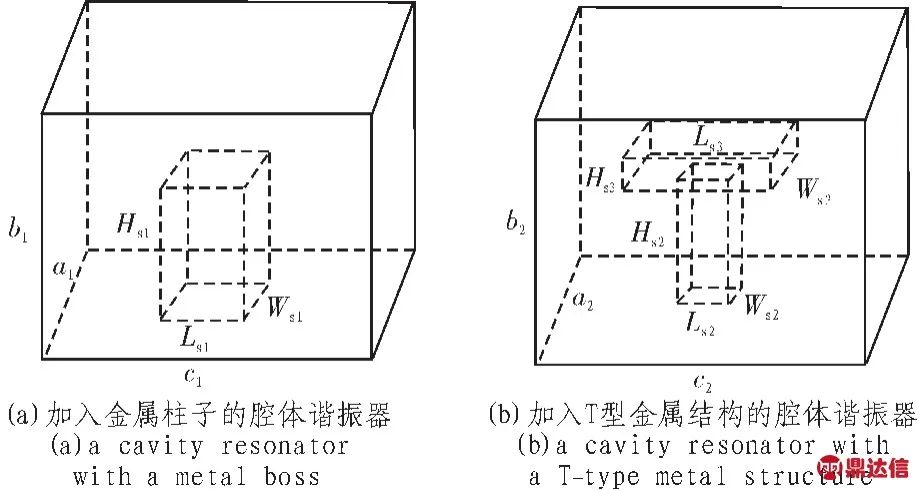
图2 腔体谐振器
Fig.2 Cavity resonator

作为例子，表1中给出了利用HFSS电磁仿真软件计算得到谐振频率为2.4 GHz的3种腔体谐振器的结构尺寸。

表1 谐振频率为2.4 GHz时3种腔体谐振器的尺寸参数
Tab.1 Size parameters of the three cavity resonators，frequency of 2.4 GHz

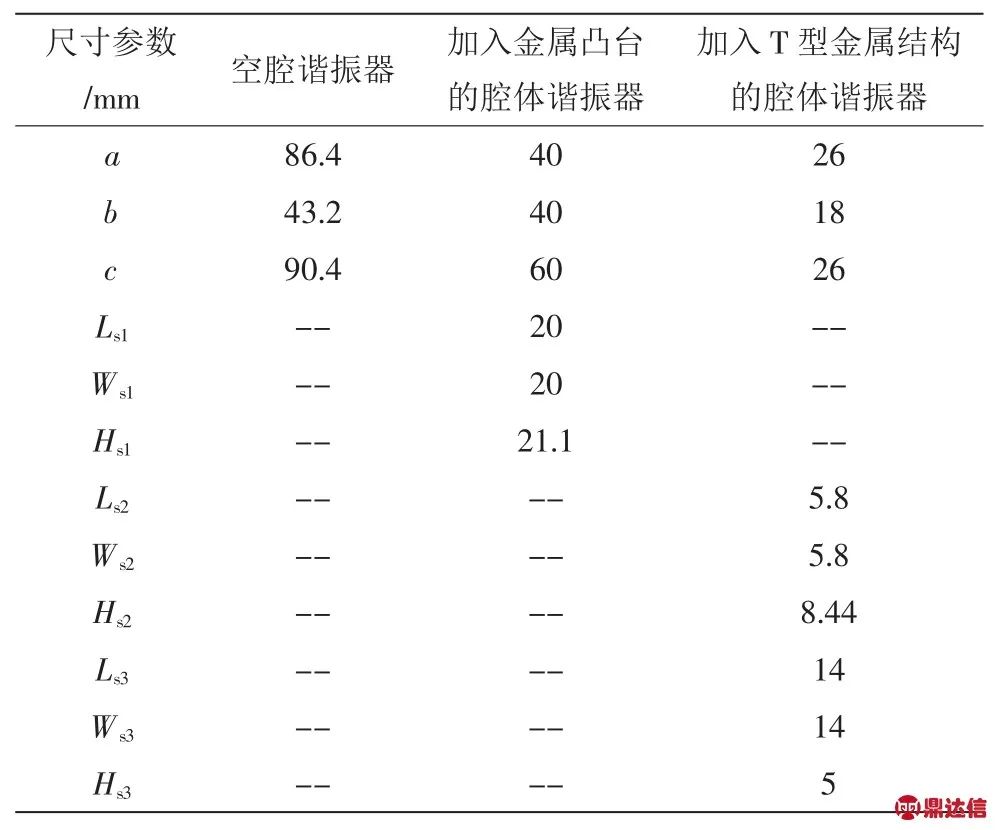
由表1可以看出，当空腔谐振器内加入金属凸台或T型金属结构时，在相同的谐振频率，腔体尺寸能够大大减小。加入T型金属结构的腔体谐振器尺寸与其他两种谐振器相比，尺寸最小。所以利用这种结构作为设计腔体滤波器的基本结构，能够有效减小滤波器体积，从而有利于其小型化应用。

2 电容加载腔体滤波器设计

文中设计的电容加载腔体带通滤波器的参数指标为：中心频率为2.4 GHz，相对带宽为10%，带外抑制为-40 dBc@2 BW，通带内波纹≤0.5 dB，插入损耗≤1 dB。根据给出的参数指标进行综合，可知滤波器采用切比雪夫型，计算得到该滤波器的阶数n=4，低通原型值为：

g0=1，g1=1.108 8，g2=1.306 1，g3=1.770 3，g4=1.818 0，g5=1.354 4。 按照以上结构，利用HFSS电磁仿真软件模拟得到了一个电容加载腔体带通滤波器。其结构示意图如图3所示，仿真曲线如图4所示。

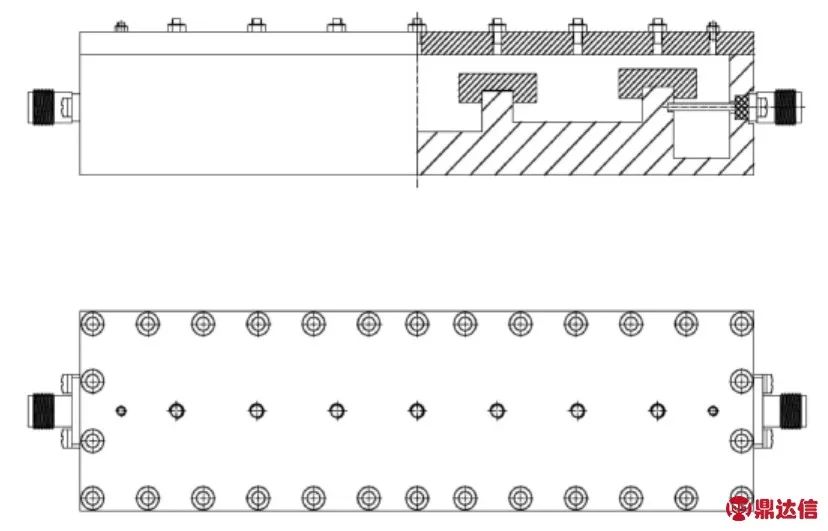
图3 电容加载腔体带通滤波器结构示意图
Fig.3 Structure diagram of the capacity-loaded cavity band-pass filter

文中另外给出了一个常规腔体滤波器的仿真结果，仿真曲线如图5所示。

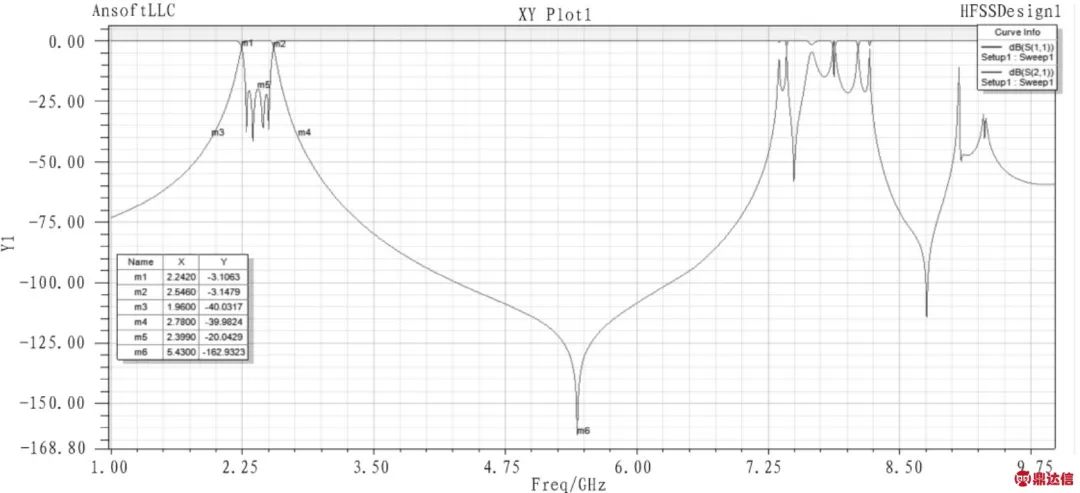
图4 电容加载腔体带通滤波器仿真曲线
Fig.4 Simulation curve of the capacity-loaded cavity band-pass filter

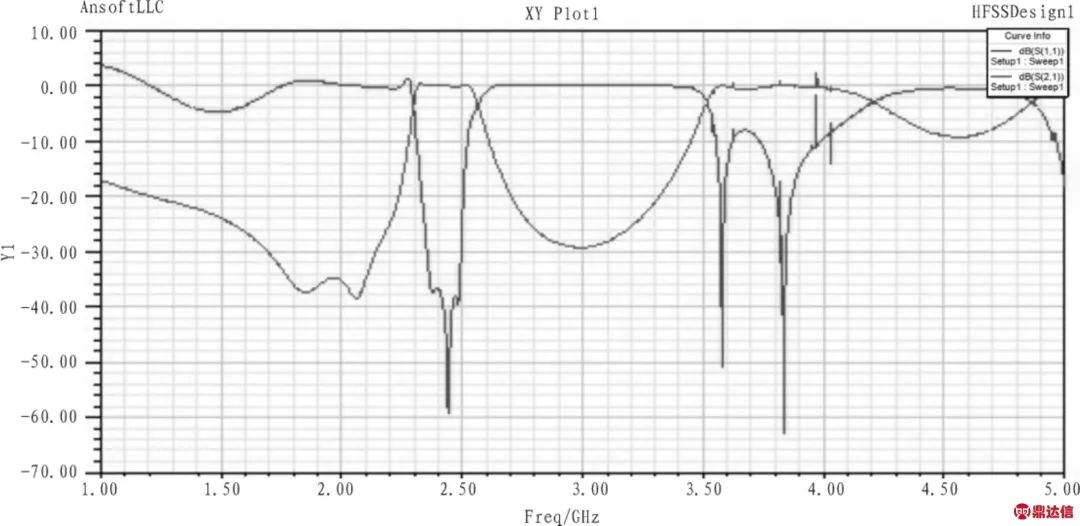
图5 普通腔体带通滤波器仿真曲线
Fig.5 Simulation curve of a traditional cavity filter

由图3可以看出，电容加载腔体滤波器由4个加载了T型金属结构的腔体与腔体之间的耦合结构构成，滤波器总长度为121.8 mm，长度和高度为34.8 mm和21 mm，而常规腔体滤波器的尺寸为：86.4 mm×43.2 mm×351.8 mm。可以看出电容加载腔体滤波器的体积大大减小。电容加载腔体滤波器中腔体间的耦合利用耦合杆实现。耦合杆的宽度与T型金属结构下端的长方体宽度相同，高度由腔体间的耦合量决定。电容加载滤波器的输入输出结构采用抽头结构，接头采用可拆卸的SMA接头。抽头探针与腔内T型结构下端的长方体金属块直接焊接。由图4仿真曲线可以看出，电容加载腔体滤波器通带内S11≤-20 dB，远端寄生通带在3倍中心频率上出现，而常规腔体滤波器的寄生通带出现在2倍中心频率处，所以采用本结构的滤波器带外抑制性能优于常规腔体滤波器。

3 电容加载腔体滤波器样品及测试

由仿真优化结果，文中加工制作出一套滤波器样品。其外观照片和内部结构照片如图6、图7所示。为了修正该滤波器的加工误差，需在滤波器的中心线上安装一排调谐螺钉。图8为该滤波器的实际测试曲线。由图8可以看出，实际加工出来的滤波器中心频率为：2.4 GHz，带宽为：240 MHz，通带内插损小于0.8 dB，驻波比小于1.25（反射系数小于-20 dB），带外抑制在1.9 GHz和2.8 GHz处都达到了40 dB。该滤波器的寄生通带出现在7.3 GHz以外。

图6 电容加载腔体带通滤波器样品照片
Fig.6 Sample’s photo of the capacity-loaded cavity band-pass filter

图7 电容加载腔体带通滤波器内部结构照片
Fig.7 Internal structure’s photo of the capacity-loaded cavity band-pass filter

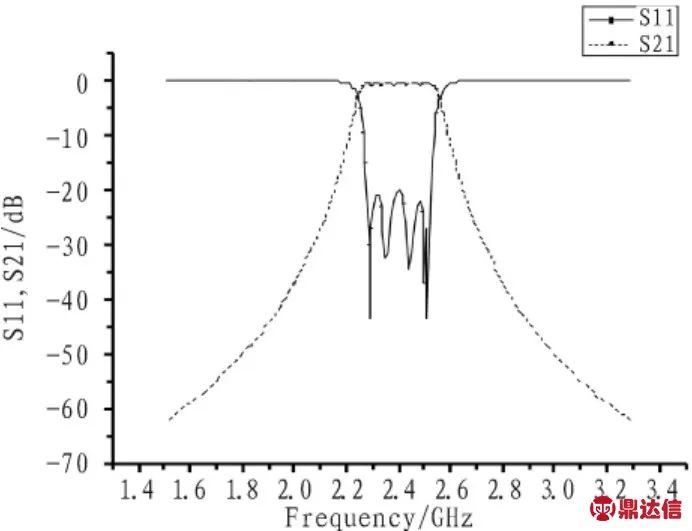
图8 电容加载腔体带通滤波器测试曲线
Fig.8 Test curve of the capacity-loaded cavity band-pass filter

4 结束语

文中介绍了一种电容加载腔体带通滤波器的设计与测试结果。首先根据传输线理论证明了采用电容加载的方式可以是传输线长度缩短。利用HFSS电磁仿真软件，仿真优化得到了一个电容加载的小型化腔体带通滤波器。通过对实际加工制作出的滤波器进行调节测试，其测试结果证明了该滤波器具有体积小，小插损，高带外抑制，寄生通带远等优点。

审核编辑：黄飞