磁力计LIS2MDL开发(2)----电子罗盘

嵌入式单片机MCU开发 2023-12-18 741

描述

概述

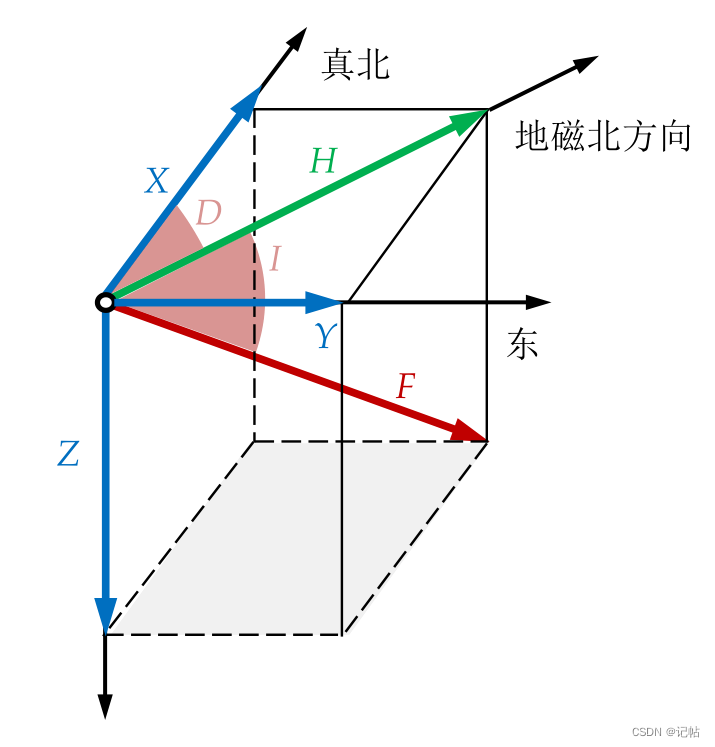
本文将介绍如何使用 LIS2MDL 传感器来读取数据来转化为指南针。地磁场强度范围约为 23,000 至 66,000 nT ，并且可以建模为磁偶极子，其场线起源于地球地理南部附近的点，并终止于磁场附近的点。磁场具有七个分量，如图所示。x，y和z分别表示北分量，东分量和垂直分量的磁场强度。H代表总水平强度，F代表磁场的总强度，而D和I分别代表磁偏角和磁倾角。

最近在弄ST和瑞萨RA的课程，需要样片的可以加群申请：615061293 。

指南针

视频教学

https://www.bilibili.com/video/BV1xG411a7cs/

样品申请

https://www.wjx.top/vm/OhcKxJk.aspx#

源码下载

https://download.csdn.net/download/qq_24312945/88634988

环境磁场建模

尽管可以选择七个不同的元素来处理给定点的磁场，但并非所有元素都是进行定位的理想选择。X，Y 和 Z 的三个元素是从磁力计获得的基本值，而其他四个元素是使用这些元素来计算的。前三个元素随移动设备方位角的改变而偏离，因此，对于许多基于磁场的室内定位系统通常假设以固定方位工作，行人可以更改方向，但不能更改设备方位。

在大地坐标系的水平面上,假设磁北和x轴的夹角为a, x方向的磁分量是Mx,y方向的分量是My,则

ɑ=arctan(My/Mx)

这是电子罗盘定向的基本原理。实际应用中,电子罗盘不能总是保持在水平面上，如下图所示一样存在俯仰角和横滚角。将罗盘坐标系下的 z轴向下, 3个轴的磁分量投影到水平面上可以得到Xh,Yh,相应的磁感应值:

Xh=Xcosф+Ysinфsinθ - Zsinфcosθ

Yh=Ycosθ + Zsinθ

相应的

ɑ=arctan(Yh/Xh)

指南针

Angle_XY=atan2( (magnetic_mG[1]-Xoffset),(magnetic_mG[0]-Yoffset) ) * (180/3.14159265)+180;//计算角度
                Angle_XZ=atan2( (magnetic_mG[2]-Zoffset),(magnetic_mG[0]-Yoffset) ) * (180/3.14159265)+180;//计算角度
                Angle_YZ=atan2( (magnetic_mG[2]-Zoffset),(magnetic_mG[1]-Yoffset) ) * (180/3.14159265)+180;//计算角度

消除硬铁误差

电子罗盘有两种工作模式，一种是正常工作模式，另一种是出厂设置模式，这种出场设置模式就是为了消除硬铁干扰。硬铁干扰产生于永久磁铁，和被磁化的金属，或罗盘平台上的钢。这些干扰会保持大小恒定，与罗盘的相对位置固定，而与罗盘指向无关。所以当罗盘安装好后，它周围的硬铁干扰就几乎不会改变了，只要对罗盘做一次准确的标定，就能很轻松的消除这项干扰。

硬铁干扰在罗盘输出的每个轴向加了一个定值，输出曲线图的圆心被移动了，对于航向的影响则是一个周期性的误差，如下图所示在理想状态时，在 360 度范围内，传感器输出极值分别为 ymax ymin xmax xmin 坐标原点为O，受到硬铁干扰后，极值变为 y'max ,y'min , x'max , x'max , 坐标原点变为O' 。要消除硬铁干扰，可以将罗盘和平台旋转一周，得到圆上的足够的点再得到圆心偏移。

指南针

具体操作过程如下：接通电源后，将罗盘匀速旋转，使微控制器采集 360 °范围内的数据，通过数值比较，找出 x 、 y 方向的极值，得出偏移坐标 O’, 即电桥的偏置电压，并将此电压值保存，每次罗盘读数时都会减去此偏移。实际上，本设计在方位角的计算过程就是此过程，所以在计算方位角的同时已经消除了硬铁干扰。这种方法也可以消除由于温度漂移产生的误差。

软铁干扰

软铁干扰来源于地球磁场和罗盘附近的任何磁性材料之间的相互作用，同硬铁材料一样，软金属也干扰地球的磁力线，不同点是，软磁的干扰程度，与罗盘的方向有关。对软铁干扰的校正，比较复杂，下面讨论采用霍尼韦尔公司的 Michal.J.Caruso 提出椭圆假设的误差补偿原理进行误差补偿的方法。

指南针

根据 Michal.J.Caruso 的研究，罗盘在理想的没有任何干扰的磁场水平面里作圆形旋转时，磁力计的显示应该呈现上图的状态，其中圆中心在 0,0 点处，每个计数代表 67微高斯，在 X 和 Y 平面中的地球磁场强度值读到 2800 个计数，约为 190 毫高斯，根据下面公式可以对每个读数确定一个方位角。

指南针

如果将磁力计安装在有发动机或者其他铁磁材料的环境中，圆形旋转时，磁力计的显示应该下图的状态。

指南针

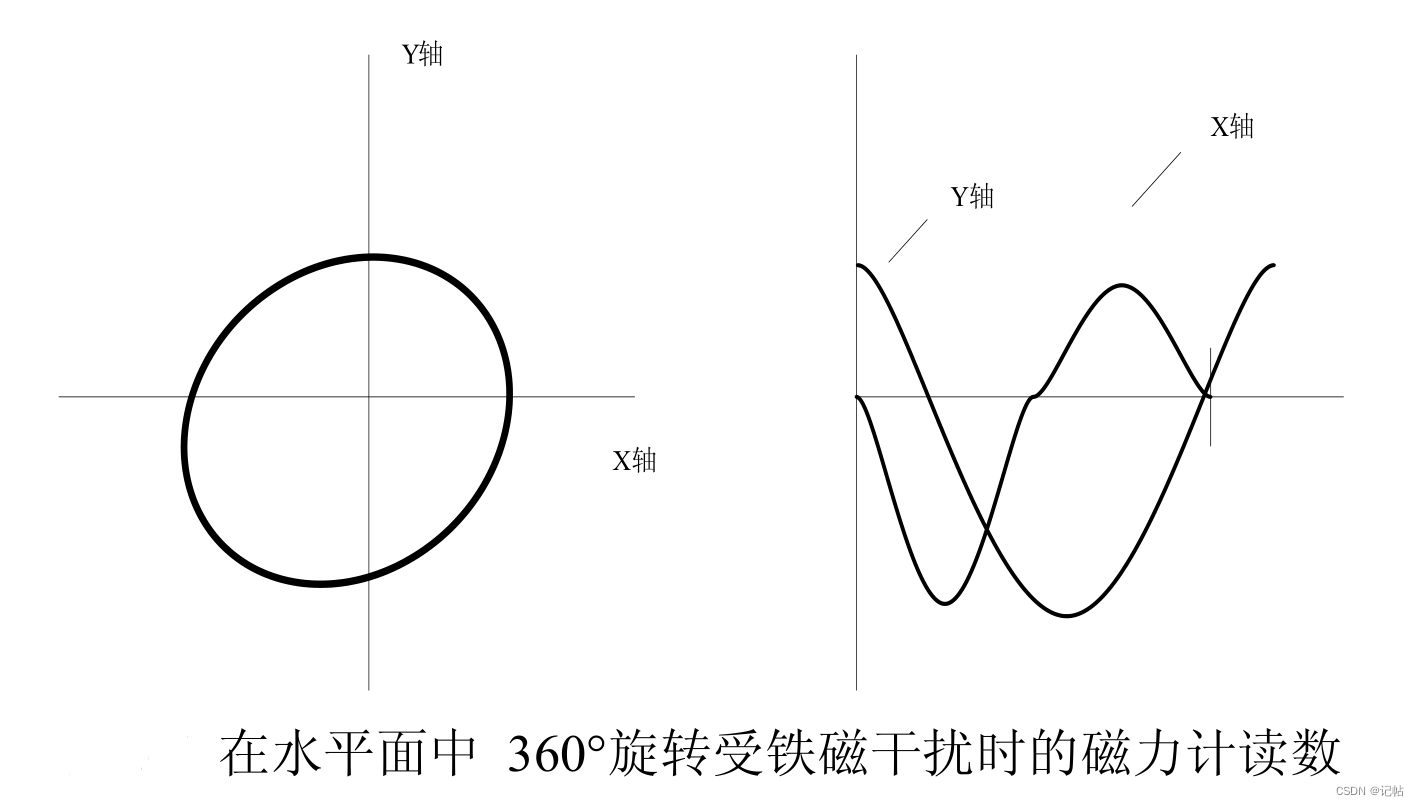
这里的图形不是一个圆 ( 有点椭圆 ) ，而它偏移 0,0 点为 -480 和 -795 个计数，这偏移和椭圆效应是干扰磁场对地球磁场作用的结果。通过确定两个定标因数 Xsf 和 Ysf 可以将椭圆改为圆。随后计算偏移值 Xoff 和 Yoff, 将圆中心定在 0,0 原点，用下面公式来计算 Y,X 值。

X 值 =Xsf×X 读数 +Xoff

Y 值 =Ysf×Y 读数 +Yoff

这里的定标因数 Xsf 和 Ysf 可由下述方法获得。

①将罗盘在水平面做旋转运动

②找出 X 和 Y 读数的最大值和最小值

③用这四个数值确定 X 和 Y 定标因数 (Xsf ， Ysf) ，以及零偏移值 (Xoff ， Yoff)

Xsf=1 或 (Y 最大 -Y 最小 )/2(X 最大 -Y 最小 )

以较大的数值为准

Ysf=1 或 (X 最大 -Y 最小 )/2(Y 最大 -Y 最小 )

以较大的数值为准

Xoff=[(X 最大 -X 最小 ) /2-X 最大 ]×Xsf

Yoff=[(Y 最大 -Y 最小 ) /2-Y 最大 ]×Ysf

主程序

在主程序中添加开机校准。

/* Infinite loop */
  /* USER CODE BEGIN WHILE */
  while (1)
  {

    uint8_t reg;
    /* Read output only if new value is available */
    lis2mdl_mag_data_ready_get(&dev_ctx, ®);

    if (reg) {
      /* Read magnetic field data */
      memset(data_raw_magnetic, 0x00, 3 * sizeof(int16_t));
      lis2mdl_magnetic_raw_get(&dev_ctx, data_raw_magnetic);
      magnetic_mG[0] = lis2mdl_from_lsb_to_mgauss(data_raw_magnetic[0]);
      magnetic_mG[1] = lis2mdl_from_lsb_to_mgauss(data_raw_magnetic[1]);
      magnetic_mG[2] = lis2mdl_from_lsb_to_mgauss(data_raw_magnetic[2]);

      printf("i=%d,Magnetic field [mG]:%4.2ft%4.2ft%4.2frn",i,magnetic_mG[0], magnetic_mG[1], magnetic_mG[2]);
            if(i< 500)
            {
                i++;
                if(magnetic_mG[0]< Xmin)
                    Xmin=magnetic_mG[0];
                else if(magnetic_mG[0] >Xmax)
                    Xmax=magnetic_mG[0];


                if(magnetic_mG[1]< Ymin)
                    Ymin=magnetic_mG[1];
                else if(magnetic_mG[1] >Ymax)
                    Ymax=magnetic_mG[1];                

                    if(magnetic_mG[2]< Zmin)
                    Zmin=magnetic_mG[2];
                else if(magnetic_mG[2] >Zmax)
                    Zmax=magnetic_mG[2];            
            }
            else if(i==500)
            {
                i++;


                Xsf = (Ymax - Ymin) / (Xmax - Xmin);
                Ysf = (Xmax - Xmin) / (Ymax - Ymin);        
                if (Xsf < 1)
                        Xsf = 1;
                if (Ysf < 1)
                        Ysf = 1;        

                Xoffset=( (Xmax-Xmin)/2 - Xmax) *Xsf;
                Yoffset=( (Ymax-Ymin)/2    - Ymax)    *Ysf;
//                Zoffset=( (Zmax-Zmin)/2    - Zmax)    *Xsf;                

            }
            else
            {
                Angle_XY=atan2( (magnetic_mG[1]-Yoffset),(magnetic_mG[0]-Xoffset) ) * (180/3.14159265)+180;//计算角度
                printf("Angle_XY=%3.2fn",Angle_XY);
//                Angle_XZ=atan2( (magnetic_mG[2]-Zoffset),(magnetic_mG[0]-Xoffset) ) * (180/3.14159265)+180;//计算角度
//                Angle_YZ=atan2( (magnetic_mG[2]-Zoffset),(magnetic_mG[1]-Yoffset) ) * (180/3.14159265)+180;//计算角度        
//                printf("Angle_XY=%3.2f,Angle_XZ=%3.2f,Angle_YZ=%3.2fn",Angle_XY,Angle_XZ,Angle_YZ);                
            }
    }        
        HAL_Delay(10);
    /* USER CODE END WHILE */

    /* USER CODE BEGIN 3 */
  }
  /* USER CODE END 3 */

审核编辑：汤梓红

打开APP阅读更多精彩内容