分数槽绕组磁势的特点

前面讲了整数槽绕组的磁势，本期继续讲分数槽绕组的磁势。

1. 分数槽绕组磁势的特点

在介绍分数槽绕组磁势之前，我们先复习一些数学基础知识。

①关于傅立叶分解。根据傅立叶极数有关知识，一个满足一定条件的周期函数可以分解为一个常数项和一系列不同周期(频率)的三角函数(正弦、余弦函数)项之和，其中周期最长(频率最低)的三角函数项的周期与被分解的函数周期相等，数学上常把这个周期最长(频率最低)的三角函数项称为基波；其余三角函数项的频率都是基波频率的整数倍，称其为谐波。谐波频率与基波频率之比称为谐波的次数，例如：谐波频率与基波频率之比为2的谐波称为二次谐波；谐波频率与基波频率之比为3的谐波称为三次谐波…。按照上述定义，谐波的次数均为整数。但是，在许多应用场合下，为了分析方便，而不将最低频率项作为基波，而是将需要重点分析的频率项作为基波，其余各项都作为谐波，这样就会出现低于基波频率的项，我们称之为次谐波，而且还会出现谐波的次数不是整数的情况，即出现分数次谐波。实际应用中，用哪一个频率作为基波频率，取决于分析时关注的重点和分析的简便性。由于电机主要依靠极对数为p的磁场实现机电能量转换，因此将极对数为p的磁场波称为工作波或称主波，主波的波长为2τ。在分析电机的电磁性能时，常用主波作为基波，分析起来比较方便；而在分析振动噪声时，常用一对极作为基波；在分析分数槽绕组的磁势时，还常用一个单元电机的弧长作为基波的周期。这样谐波的次数就不会出现次谐波和分数次谐波，使得计算更加简便。

②关于谐波次数问题。我们曾在第一三一期——《电机绕组(8)》中讲到，如果周期函数满足f(x)=-f(x+T/2)，即称之为奇谐函数，奇谐函数做傅立叶分解时，只含有奇次谐波，而无偶次谐波；如果周期函数满足f(x)=f(x+T/2)，则称之为偶谐函数，偶谐函数做傅立叶分解时，只含有偶次谐波，而无奇次谐波；如果周期函数不满足以上两种情况，则这种函数即不是奇谐函数，也不是偶谐函数，其做傅立叶分解时，就即含有奇次谐波，又含有偶次谐波。

了解了上述数学基础知识，接下来我们就分析整数槽绕组与分数槽绕组磁势的特点。

对于整数槽绕组，每极每相槽数q=整数，每对极下各相载流导体的安导波分布情况都是重复的，因而每对极下多相合成磁势的波形也是重复的，且N极与S极下的磁势大小相等、方向相反。也就是说，整数槽绕组的磁势，在空间分布上是一个以2τ为波长(周期)，极对数(频率)为p的奇谐函数，将这样一个周期函数作傅立叶分解，得到的最小频率为p，如果将其定义为基波，即基波磁势的波长为2τ，其他各项为谐波，则各谐波的次数均为整数，且谐波的次数仅存在奇次的高次谐波，而无偶次谐波。另外对于三相对称绕组，其磁势中也不包括三及三的整数次谐波。

对于分数槽绕组，每极每相槽数q=b+c/d=N/d，为一不可约的分数，其中：N=b•d+c，称其为分数槽绕组的每极每相等效槽数，N与d不可约。这就意味着每个极下分配给每相的槽数不是整数，而是d个极下每相才能得到整数N个槽，因此各个相带内的极相组有大有小，相邻两对极下的安导波分布不相重复，只有经过一个单元电机后，安导波分布才重复一次，这就意味着分数槽绕组的磁势是以一个单元电机的弧长为波长的周期函数，因此分数槽绕组的磁势作傅立叶分解后，波长最大的一项其周期(波长)为一个单元电机的弧长，即最低频率为单元电机的个数t，如果将其作为基波，其他项作为谐波，则谐波的次数就全部为整数，但此时基波的频率并不是主波的极对数p，而是t，在这种定义下，主波变成了p/t次谐波；如果将主波作为基波，其他各项作为谐波，则谐波的次数就会出现分数次谐波和次数小于1的次谐波，而且谐波的次数还与q的分母d是偶数还是奇数有关。由此可见，与整数槽绕组相比，分数槽绕组的磁势具有一系列的独有的特点，其谐波含量要丰富得多，分析起来也更加复杂得多。下面先按照d是偶数还是奇数，分两种情况说明分数槽绕组磁势的谐波次数，然后再分析其幅值。

2. d为偶数时磁势的谐波次数

若d为偶数，则每 d 个极就组成一个单元电机，所以每经过d个极，安导波及其所产生的磁势波的波形将重复一次。将磁势波进行傅立叶分解，若以单元电机在定子内圆所占弧长 d•τ作为基波波长，则磁势的谐波次数 n′ 应为：

n′=1,2,3,4,5,6,… (1) 由于在一个周期d•τ范围内，前半个周期(d/2)•τ内的安导波分布与后半个周期(d/2)•τ内的安导波分布即不满足奇谐函数的条件，也不满足偶谐函数的条件，也就是说，当d为偶数时，安导波即不是奇谐函数也不是偶谐函数，相应产生的磁势同样即不是奇谐函数也不是偶谐函数，因此磁势的谐波中既有奇次谐波又有偶次谐波，但谐波次数 n′ 均为整数。由于主波波长为2τ，所以此时主波将成为d/2次谐波。

若改以主波作为基波，则其他各次谐波的次数υ就成为：

υ=n′/(d/2)=(2/d)•(1,2,3,4,5,6,…) (2) 此时υ既可能是整数，也可能是分数；既可能大于1，也可能小于1。换言之，用主波作为基波时，分数槽绕组的磁势中既可能有高次谐波，也可能有低次和分数次谐波，次数低于主波(υ<1)的低次谐波，通常被称为次谐波。

以一台 Z1 =540槽、2p=48、 q=3+3/4的三相水轮发电机的定子绕组为例，该绕组的d=4。由于Z1与p之间具有最大公约数12，所以整个电机可以分成12个单元电机(即t=12)，每个单元内有4极、45槽。图1所示为定子 A 相电流达到最大值时，一个单元电机内三相合成磁势的分布。

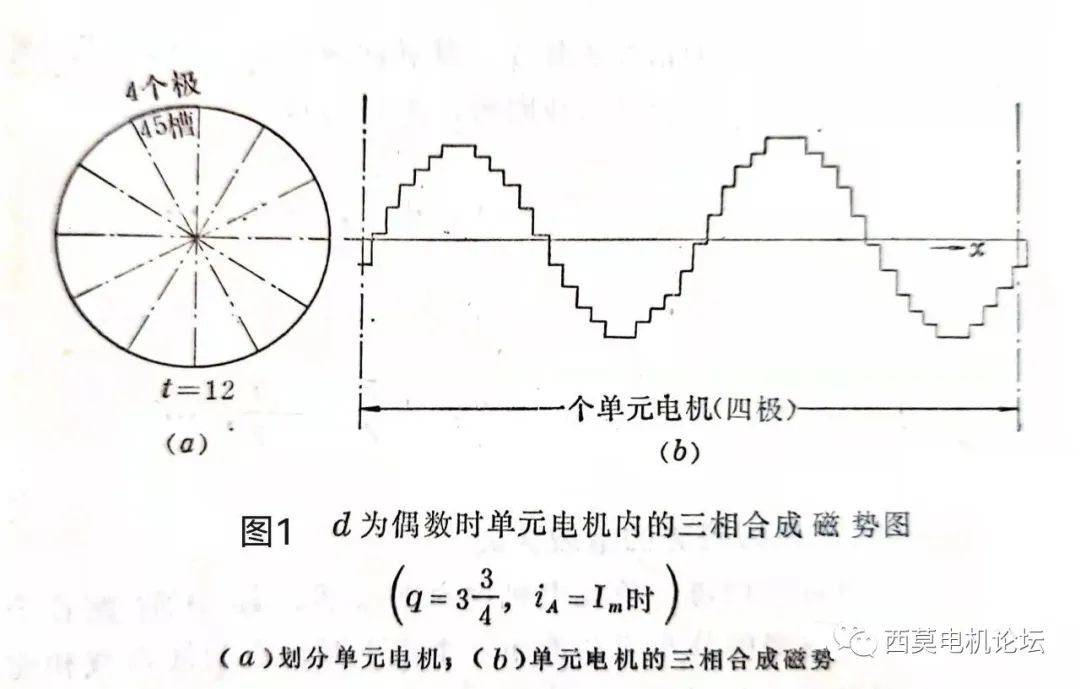从图1可知，每隔四个极,合成磁势的分布波形将重复一次,故以4τ作为基波波长进行谐波分析时，谐波次数 n 应为：

n′ =1,2,3,4,5,6,…

此时所有的谐波次数均为整数；对于波长为2τ的主波，此时将是二次谐波。

若以2τ作为基波波长，则主波成为基波，其他谐波的次数 υ 将成为：

υ=n′/(d/2)=(1/2)•(1,2,3,4,5,6,…)

=1/2, 1, 3/2, 2, 5/2, 3，…

此时将出现 υ 为1/2、3/2等分数次谐波。

以上是一般情况。若绕组为三相对称，定子电流也是三相对称，则合成磁势中也不存在n′=3以及3的整数倍的谐波。若规定主波的转向正，则与主波相邻的其他谐波的转向为正、反相间，于是就有：

n′=-1, +2, -4, +5,…

或：

υ=-1/2, +1, -2,+5/2, …

其中：n′=+2或υ=+1的谐波为主波；“+”表示该次谐波与主波转向相同；“-”表示该次谐波与主波转向相反。

3. d为奇数时磁势的谐波次数

若 d =奇数，则每一单元电机内有2d个极，其中后面 d 个极下的安导波和磁势波，应与前面 d 个极下对应点的安导波和磁势波大小相等、方向相反，也就是说，d为奇数的分数槽绕组，其安导波和磁势波均为奇谐函数。因此，用单元电机弧长2d•τ 作为基波波长来进行谐波分析时，磁势波形中将仅含有奇次谐波，即：

n′=1,3,5,7,… (3) 此时主波的次数为d 。

若改以主波为基波，则谐波的次数 υ 将成为：

υ=n′/d=(1/d)•(1,3,5,7,…) (4) 同理，三相对称运行时，不存在 n′=3及其倍数次的谐波。谐波磁势的转向，与 d =偶数时同样确定。

以一台 Z1 =456、2p=56、q =2+5/7的三相水轮发电机的定子绕组为例，该绕组的 d =7(奇数)。由于 Z1 与 p 之间具有最大公约数4，故整个电机可分为4个单元电机(即 t =4)，每个单元电机有14个极，114槽。图2表示 A 相电流达到最大值时，一个单元内的三相合成磁势。

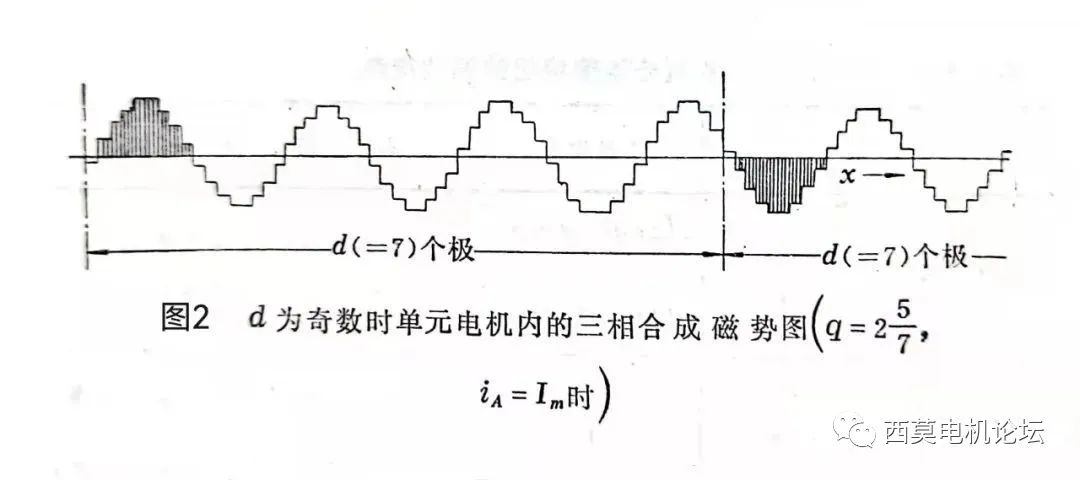
由图2可见，后面7个极的磁势波形与前面7个极的磁势波形恰好反向，此时若以14τ作为基波波长来进行谐波分析，合成磁势中将仅含有整数次的奇次谐波，即：

n′=+1,-5,+7,-11,+13,…

其中+7次谐波为主波。

若以主波作为基波，则谐波次数 υ 应为：

υ=n′/7=+1/7,-5/7,+1,-11/7,+13/7,…

即谐波次数将出现分数次。各次数前面的正负号所代表的意义同上。

4 用二极波作为基波时的谐波次数

通常情况下，都是把电机中的主波作为基波，即以2τ作为基波波长，这样做对于研究整数槽绕组和发电机的电势波形问题都非常方便。对于分数槽绕组，为避免把磁势的谐波次数写成分数形式，常以单元电机的弧长作为基波波长，此时主波成为 d(或d/2)次谐波。

除了这两种方式以外，谐波次数还有第三种表达方式。在分析振动和噪音问题时，常以整个电机的周长 πD 作为基波的波长，即以二极波作为基波。由于 πD=p•2τ，故采用此种方式表达时，主波就成为p次谐波。以六极电机(p=3)为例，电机中的主波为六极波。若以六极波作为基波，则主波即为基波(即υ=1)；若以二极波作为基波，则主波成为三次谐波(即 n=3)。图3用图形表示了用主波或二极波表示时，谐波次数υ和n之间的关系。

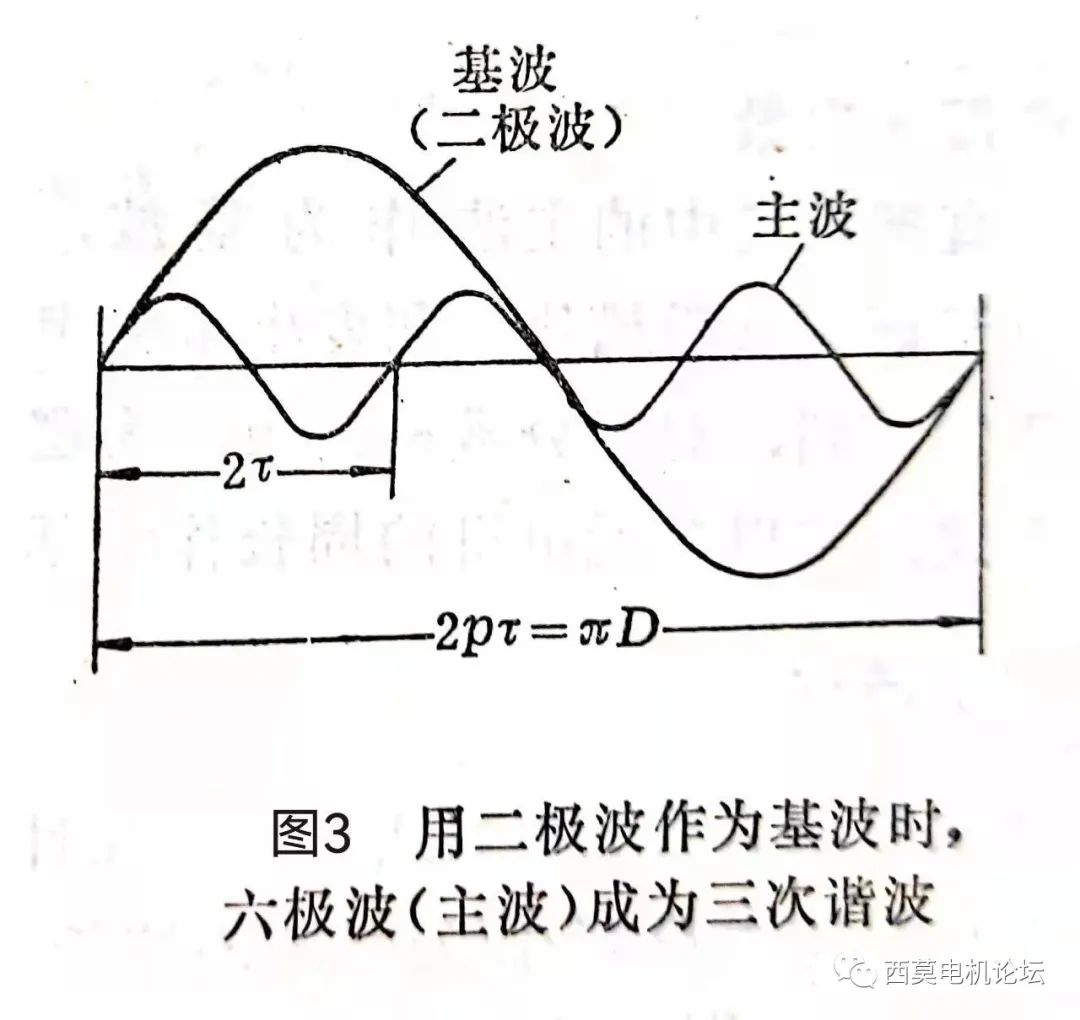不难看出，用二极波表示时，谐波次数 n 应为：

n=p•υ (5) 上述三种方式表达时，双层分数槽绕组的谐波次数见表1。

5 不同文献中分数槽绕组磁势谐波次数的计算公式

关于分数槽绕组磁势谐波次数的描述和计算，在不同的文献中有不同的分析方法和计算公式，上述介绍的计算方法与1983年水利电力出版社出版，由汤蕴璆、史乃、沈文豹所编的《电机理论与运行》中所述是一致的。为了便于同学们阅读和理解不同文献中关于分数槽绕组磁势谐波的相关内容，现将收集到的各种文献中关于分数槽绕组磁势谐波的计算公式列于表2，并以实例对各文献中公式的正确性予以验证。

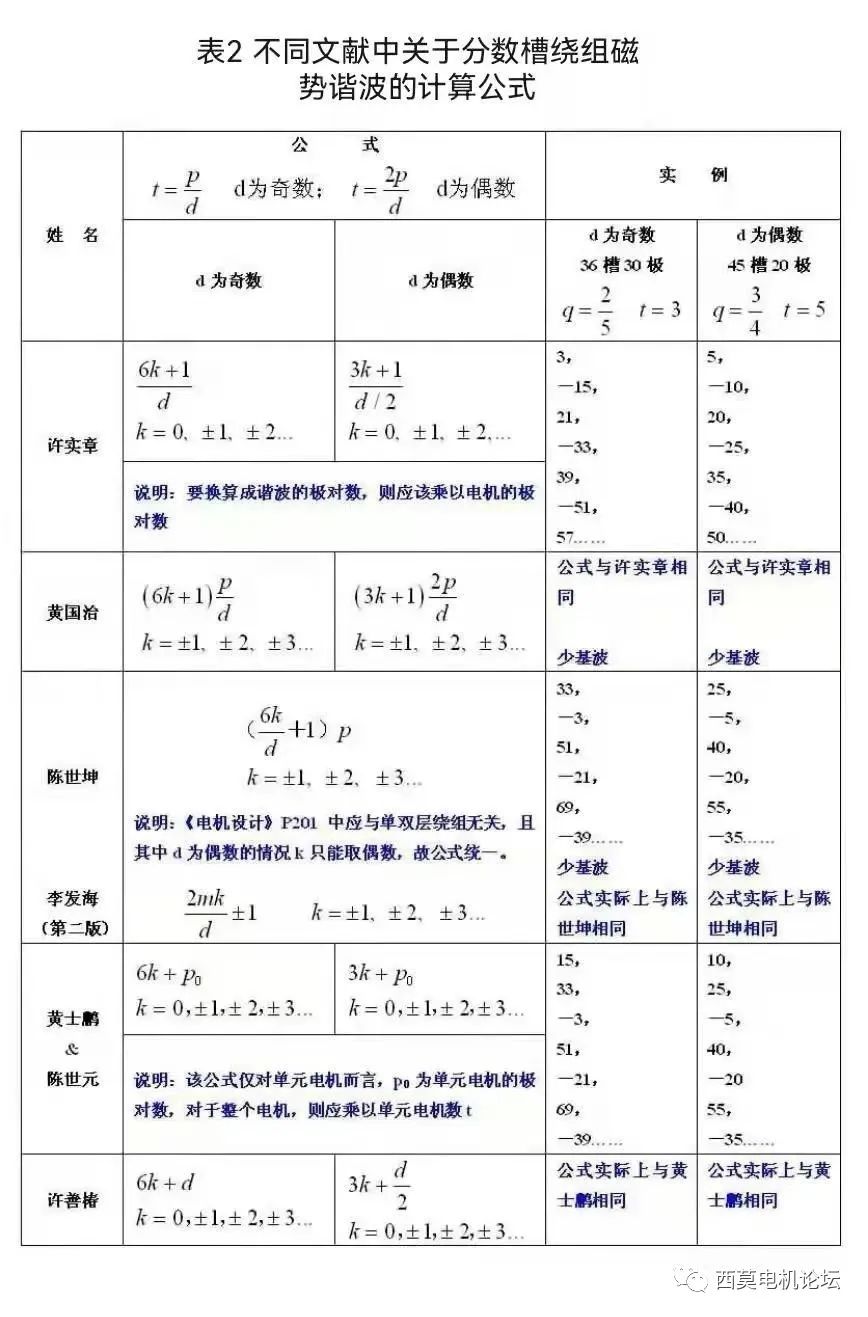
【注】表中文献：许实章《交流电机绕组理论》；黄国治《Y2系列技术手册》；陈世坤《电机设计》第2版；李发海等《电机学》第2版；黄士鹏、陈世元《交流电机绕组理论》；许善椿、金波交流电机定子分数槽绕组的谐波磁势问题[J].大电机技术,1999,000 (003 ):1-5.。

通过分析和验证，也发现某些文献中的分析和描述存在一些错误，例如：陈世坤《电机设计》p201，就存在错误，分单双层绕组进行讨论，其实分数槽绕组的谐波次数与绕组的单、双层是没有关系的，而是跟q的分母是奇数还是偶数有关；此外黄士鹏、陈世元的《交流电机绕组理论》，里面对于分数槽的谐波极对数分析，其实仅对单元电机是正确的，对于非单元电机显然还要乘以单元电机数t。

小结：各种文献中虽然分析方法和计算公式不同，某些描述甚至存在一些小错误，但经过必要的修正后，基本上均是正确和一致的。其中许实章与黄国治两位教授所著文献中的公式基本相同，且与李发海等教授的文献描述本质上是相同的；而其余三个文献本质上也是相同的。

6. 定子磁动势的幅值

与整数槽绕组相似，以主波作为基波时，分数槽绕组的三相基波合成磁动势的幅值 F1 (安匝/极)应为：

F1=1.35•I•(Kdp1•W1)/p (6) 类似地，三相谐波合成磁动势的幅值 Fυ为：

Fυ=(1/υ)•1.35•I•(Kdpυ•W1)/p (7) 式中：W1为定子每相串联匝数；Kdp1为基波的绕组系数；Kdpυ 为 υ 次谐波的绕组系数。

与整数槽绕组相同，分数槽绕组的绕组系数也等于短距系数与分布系数的乘积，即Kdpυ=Kdυ•Kpυ，对于短距系数Kpυ，分数槽绕组与整数槽绕组的短距系数计算公式相同，即：Kpυ=sin[υ(Y1/τ)90º]；而对于分布系数Kdυ，分数槽绕组的计算要比整数槽绕组复杂得多，对此，汤蕴璆教授早在1973年第3期的《大电机技术》上发表过一篇文章《分数槽绕组的分布系数》，在这篇文献中有详细的推导过程。这里推导过程略去，只讲一下分数槽绕组分布系数的最终计算公式。

对于60相带、具有“最大分布因数”的三相分数槽绕组，其各次磁势谐波(包括基波υ=1)的分布系数为：

Kdυ=sin(N•αυ/2)/[N•sin(αυ/2)] (8) 式中：N为每极每相的等效槽数，N=b•d+c；角度αυ分两种情况：

①当 d =偶数时：

αυ=D•d•αm•υ+180º (9) ②当 d =奇数时，又分两种情况：

P为偶数时：

αυ=D•d•αm•υ (10) P为奇数时：

αυ=D•d•αm•υ+180º (11)

其中：αm=60º/N；D=(3N•P+1)/d；P为使D成为整数的最小整数。式⑻对任何次数(高次或低次、整数或分数次)的谐波都适用。

由以上各式可知，分数槽绕组的分布系数Kdυ除与谐波次数υ 有关外，还与每极每相槽数q 中的分母 d 以及 P 值的奇偶性有关。经过进一步推导，若仅考虑数值而不考虑正、负号时，式⑻可简化为：

d=偶数时：

Kdυ=1/[2N•cos(D•n′•60º/N)] (12)

d=奇数且P=偶数时：

Kdυ=1/[2N•sin(D•n′•30º/N)] (13)

d=奇数且P=奇数时：

Kdυ=1/[2N•cos(D•n′•30º/N)] (14)

式中，n′为与υ相对应的谐波次数，见式⑵和式⑷：当d=偶数时，n′=υ•d/2；当d=奇数时，n′=υ•d 。

本期介绍了分数槽绕组的磁势，与整数槽绕组相比，分数槽绕组的磁势谐波更加丰富，除了有高次谐波外，还含有次数低于主波的次谐波和分数次谐波，在某些情况下，定子磁势的次谐波与主极磁场相互作用，可使凸极同步电机的定子铁心产生显著的振动，在绕组设计时必须引起高度重视。

　　审核编辑：汤梓红