

深入研究高考电磁学问题研究
描述
摘 要
随着高中物理新教材的使用以及新高考在全国的陆续施行,对高中物理教学而言,无论是教学内容还是教学形式都出现了许多新的课题。这就使得站在高观点下(即大学普通物理学角度)研究高中物理,不仅成为教学改革的迫切任务,也成为了新课程下物理教学改革的一个主流方向。
本文将以 2020 年高考全国甲卷第 21 题和 2020 年高考全国乙卷第 20 题为例,从大学电磁学视角分析高考电磁学的问题,旨在引导物理专业的师范生要认真学好专业课程,提高自身的物理素养,能站在高观点下审视高中物理的内容,解决教学中的疑难问题。另外,希望中学的一线教师,要终身学习,不断重温大学的物理课程,站在高观点下审视高中物理的内容,不断解决教学中的疑难问题,使自己的教学更具有针对性和创造性,不断地提高教育教学水平,向更高的层次迈进,促进学生核心素养的全面提升。
问题一 电磁滑杆问题
在研究电磁滑杆问题时,高中阶段所求解的内容往往是时间趋于无穷时的极限情况,即金属杆的最后状态。教师往往忽略了对中间过程的分析,忽视了对学生极限思维的培养。下面我们以 2020 年全国甲卷第 21 题为例,运用高等数学手段对金属框、导体棒运动情况的变化作全程分析。原题如下:
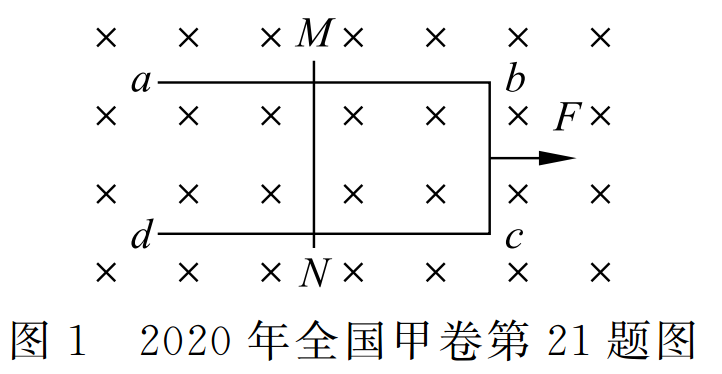
如图 1 所示,U 形光滑金属框 abcd 置于水平绝缘平台上,ab 和 dc 边平行,和 bc 边垂直。ab、dc 足够长,整个金属框电阻可忽略。一根具有一定电阻的导体棒 MN 置于金属框上,用水平恒力 F 向右拉动金属框,运动过程中,装置始终处于竖直向下的匀强磁场中,MN 与金属框保持良好接触,且与 bc 边保持平行。经过一段时间后
A.金属框的速度大小趋于恒定值
B.金属框的加速度大小趋于恒定值
C.导体棒所受安培力的大小趋于恒定值
D.导体棒到金属框 bc 边的距离趋于恒定值
定性分析:设 bc 边的长度为l,导体棒的电阻为 R。设金属框、导体棒的质量分别为 m1、m2,某时刻的速度分别为 v1、v2,加速度分别为 a1、a2。对金属框、导体棒,根据牛顿第二定律,有
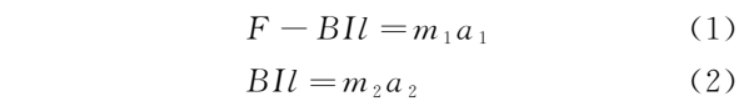
感应电流为
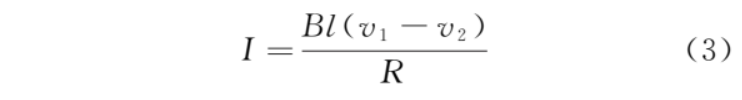
感应电流从 0 开始增大,则 a1 从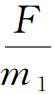 开始减小,a2 从 0 开始增大,加速度差为
开始减小,a2 从 0 开始增大,加速度差为
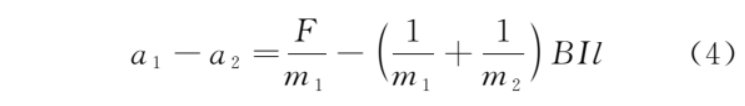
感应电流从 0 开始增大,则加速度差减小,当差值等于 0 时,由式 (1) 和式 (2),得
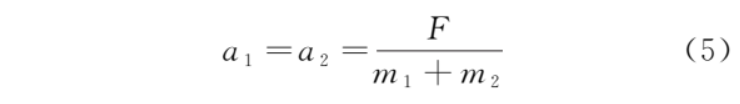
由式 (3) 和式 (4),得
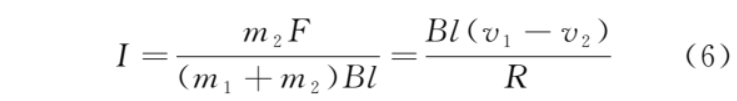
从而速度差为
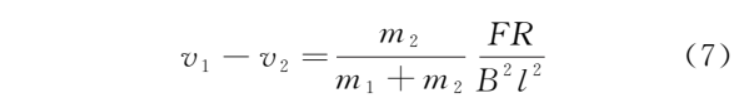
此后金属框与导体棒的速度差维持不变,感应电流不变,导体棒受到的安培力不变,加速度不变。A 选项错误,B、C 选项正确。金属框与导体棒的速度差不变,但导体棒的速度小于金属框的速度,导体棒到金属框 bc 边的距离越来越大,D 选项错误。
高中阶段用定性分析解释,大部分学生是可以理解和接受的,但是从定量的角度似乎更有“说服力”,虽然定量计算超出了高中知识范围,不过作为教师,我们不仅要知其然,更要知其所以然。下面我们做定量研究,以起抛砖引玉之效。
定量研究:以金属框、导体棒组成的系统为研究对象,根据动量定理,有
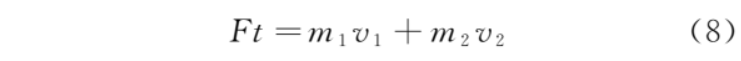
则
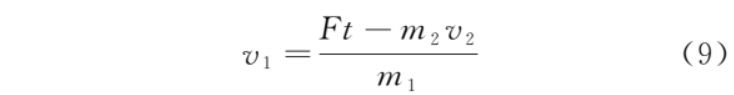
两杆所受安培力大小均为
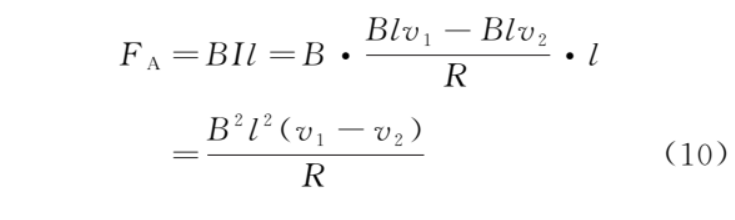
对导体棒,根据牛顿第二定律,有
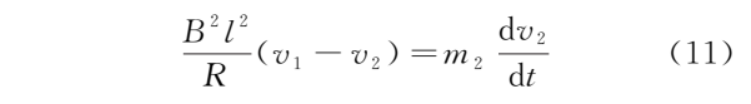
由式 (9) 和式 (11) 得关于 v2 的微分方程
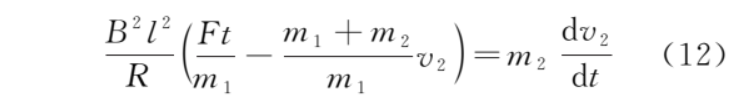
初始条件为
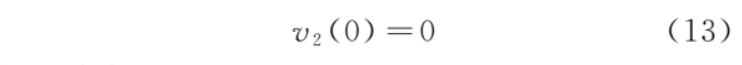
解微分方程,得
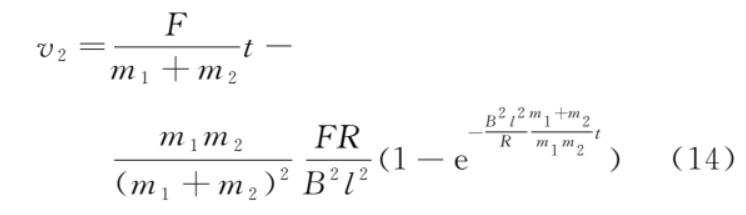
所以
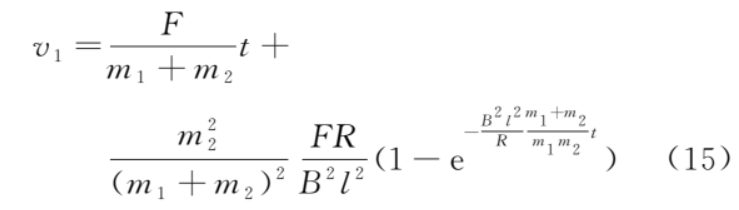
加速度
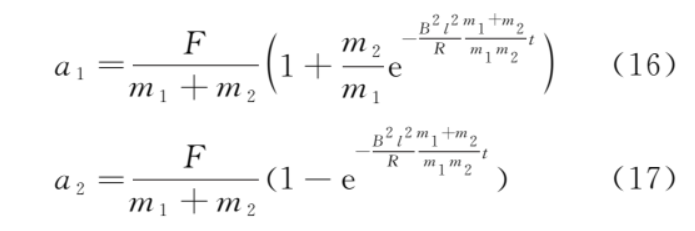
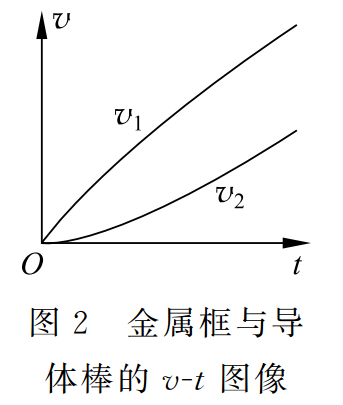
从式 (16) 和式 (17) 我们可以看出,金属框做加速度减小的加速运动,导体棒做加速度增大的加速运动。当时间 t→∞ 时,a1 和 a2 趋于稳态值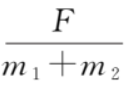 。金属框、导体棒的 v-t 图像如图 2 所示,由式 (14) 和式 (15),可得速度差为
。金属框、导体棒的 v-t 图像如图 2 所示,由式 (14) 和式 (15),可得速度差为
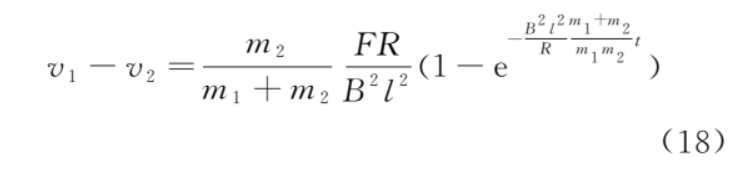
当时间 t→∞ 时,速度差趋于稳态值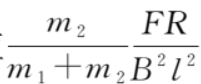 。
。
问题二 带电圆环的电场强度问题
2020 年高考全国乙卷第 20 题以均匀带电圆环为背景,不仅考查了静电场中电场强度和电势的叠加,而且也考查了核心素养中的物质观念、模型构建、科学推理和科学论证。原题如下:
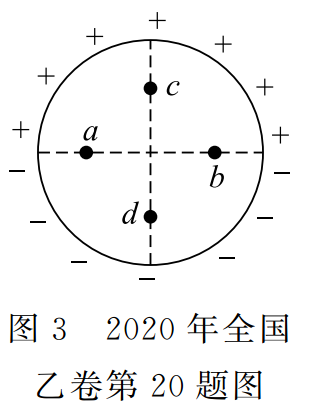
如图 3 所示,竖直面内一绝缘细圆环的上、下半圆分别均匀分布着等量异种电荷。a、b 为圆环水平直径上的两个点,c、d 为竖直直径上的两个点,它们与圆心的距离均相等。则
A.a、b 两点的场强相等
B.a、b 两点的电势相等
C.c、d 两点的场强相等
D.c、d 两点的电势相等
下面运用大学电磁学知识,对 a、b、c、d 四点的电场强度作定量研究。
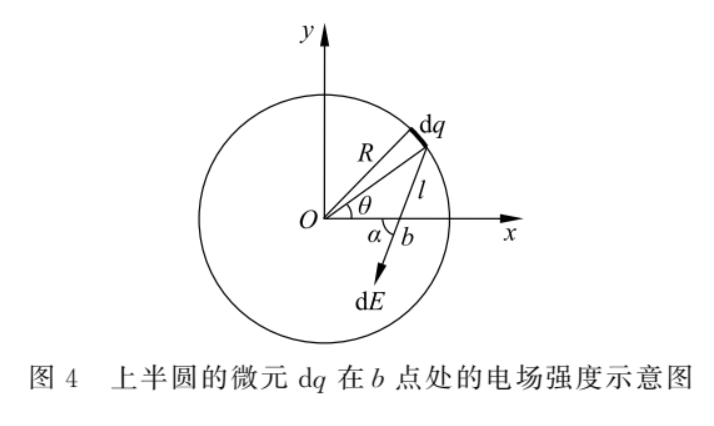
如图 4 所示,设细圆环的半径为 R,电荷线密度为 λ,b 点距圆心 O 为 r(r
根据余弦定理,有
上半圆的微元 dq 在 b 点的电场强度为
电场强度平行于 y 轴的分量为
从而
根据对称性,上、下半圆对称位置的微元 dq 在 b 点产生的电场平行于 x 轴的分量等值反向,所以 b 点的电场强度为
同理可得 a、c、d 三点的电场强度。
若上、下半圆带等量同种正电荷,a、b、c、d 四点的电场强度又该如何呢?在实际求解中,要用到一类特殊的积分——椭圆积分。椭圆积分是一种特殊函数的积分,不能用普通的积分方法来求解。它只能用二项式定理展开,得出一个收敛级数,并逐项加以积分,至于取项数的多少,视结果的精度需要而定。常用的全椭圆积分有三类,它们的解分别是
1) 第一类全椭圆积分
2) 第二类全椭圆积分
3) 第三类全椭圆积分
它不能写成幂级数的形式。下面我们来作具体的分析。
根据对称性,上、下半圆对称位置的微元 dq 在 b 点产生的电场平行于 y 轴的分量等值反向,故
从而
其中
令 θ=π+2φ,并且利用式 (25) 和式 (27) 则
其中,
除此以外,还有一些类似的高考题需要探讨。尽管在高中阶段我们不要求学生作上述的定量研究,但作为一名优秀的物理教师,在给学生一碗水的同时,自己得有一桶水。所以我们对一道试题既要有让学生理解并掌握的定性分析,还要有能让自己信服的定量研究。只有处理好定性与定量的关系,站在高观点下看问题,才能对问题的认识更加深入透彻,讲解得更加得心应手。
审核编辑:黄飞
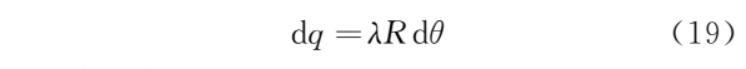
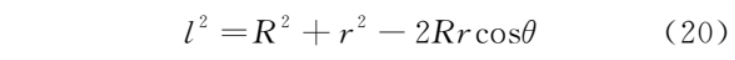
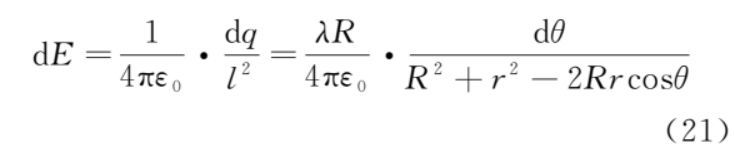
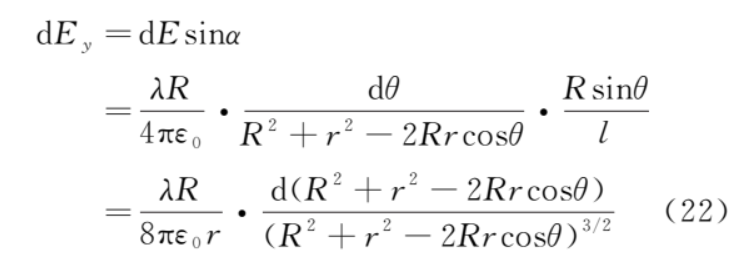
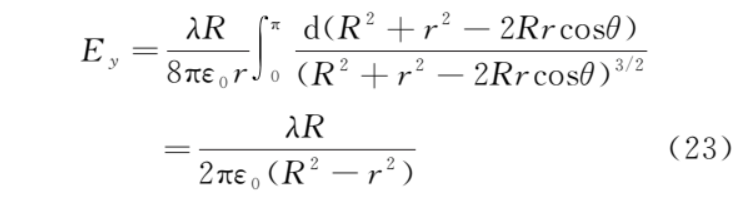
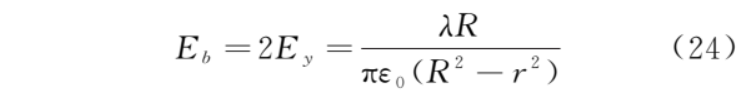
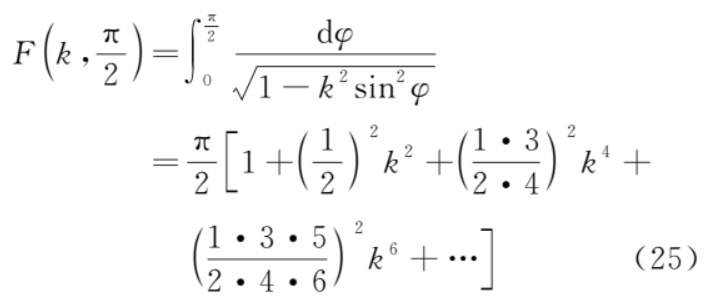
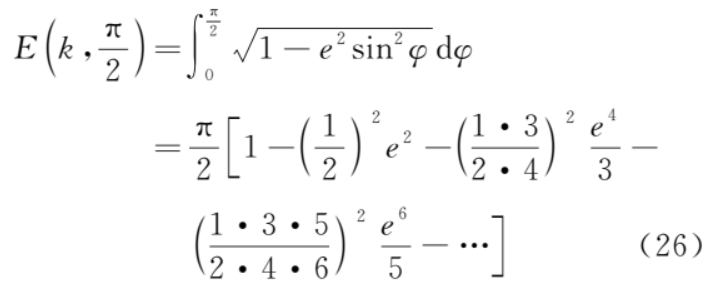
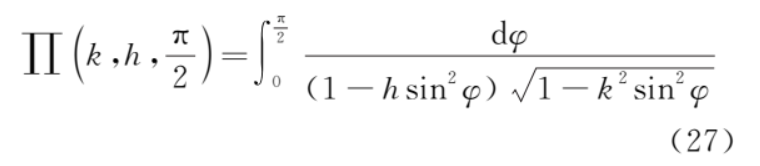
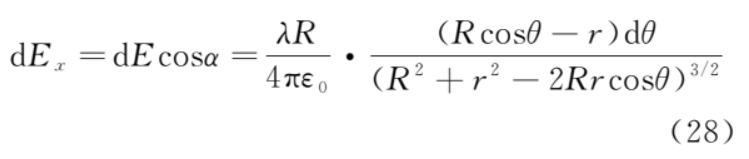
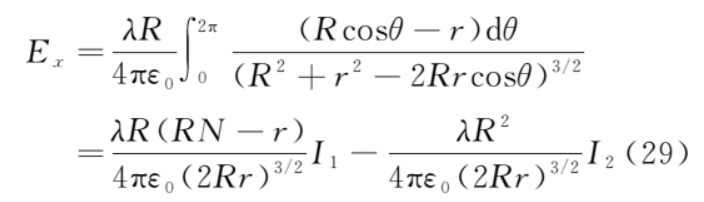
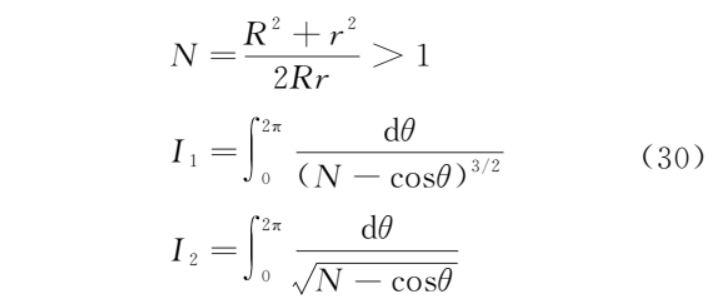
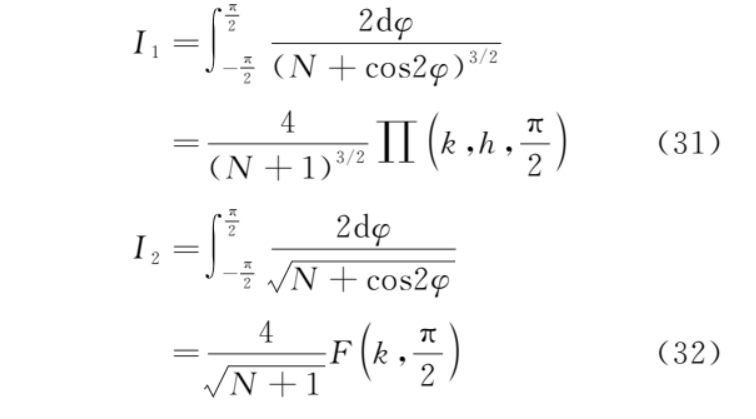
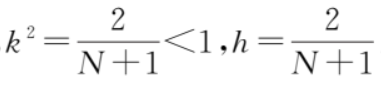 。
。
-
电磁学、磁电学与磁电子学是一回事吗2023-11-20 2477
-
深入研究彻底掌握设备树2022-02-17 862
-
电磁学的介绍和近代研究史2021-05-13 6284
-
电磁学的发展历史详细概述2020-11-13 1818
-
电磁场理论与计算电磁学的学习课件免费下载2019-11-13 1480
-
电磁学理论的建立2019-07-02 1919
-
计算电磁学的几种方法的区别介绍2019-06-28 3689
-
电磁学复习提纲2017-05-18 1134
-
计算电磁学讲义2014-04-19 4145
-
电磁学课件练习题 (电磁学习题集解答)2010-07-17 823
-
电磁学的数学基础2009-08-22 684
-
ec电磁学计算软件 -下载2009-05-15 12418
-
linux的深入研究2009-03-28 339
全部0条评论

快来发表一下你的评论吧 !

