GPT推断中的批处理（Batching）效应简析

机器学习模型依赖于批处理（Batching）来提高推断吞吐量，尤其是对于 ResNet 和 DenseNet 等较小的计算机视觉模型。GPT 以及其他大型语言模型（Large Language Model, LLM）是当今最热门的模型。批处理对于 GPT 和大语言模型仍然适用吗？让我们一探究竟。    

背景知识

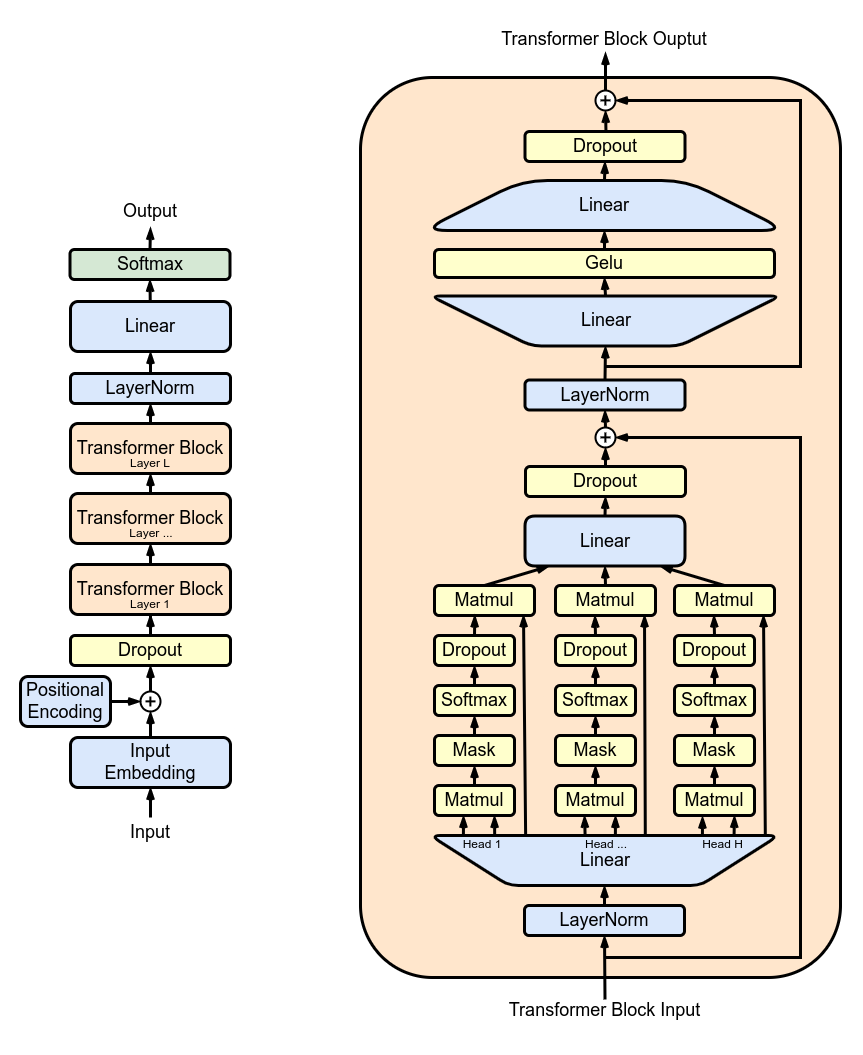
上图来源于维基百科 [1]，展示了 GPT 的整体架构和一个 Transformer 层。让我们简化对 GPT 的理解。GPT本质上是一堆 Transformer 层的堆叠。由于每个 Transformer 层的架构相同，我们将重点放在单个 Transformer 层上。一个 Transformer 层包括三个部分：密集层投影（Dense Layer）、自注意力机制（Self-Attention）和前馈网络（Feed-Forward-Network）（即两个密集层）。  

为简单起见，我们将忽略与计算和输入输出相关的一些次要细节，如层归一化（LayerNorm）、掩蔽层（Mask）、暂退层（Dropout）以及残差连接（Residual Connection）。相反，我们将专注于分析矩阵乘法。如果你想更深入地了解 GPT 架构或自注意力机制，我建议阅读本文末尾列出的论文和博客文章。  

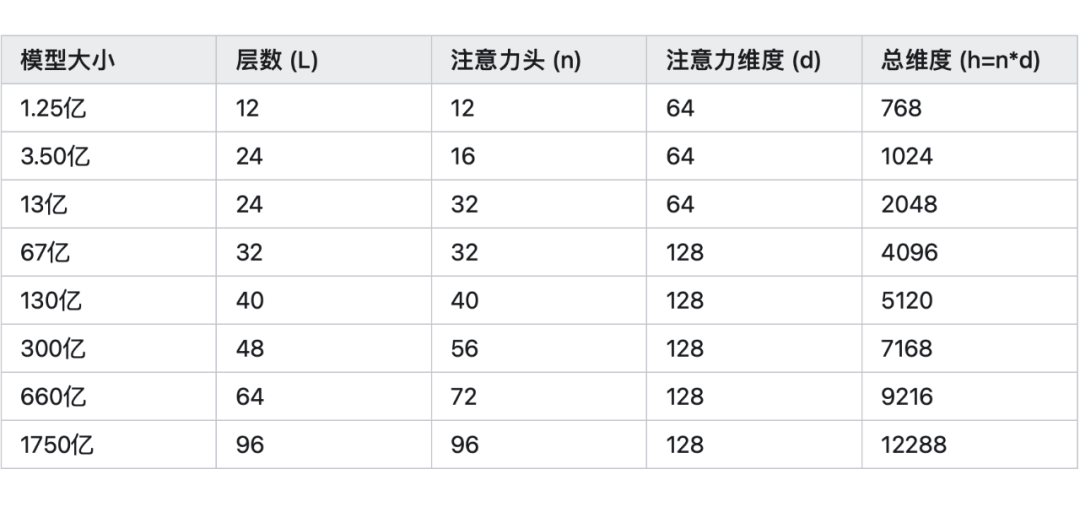
GPT 模型有不同的尺寸，参数数量从 1.25 亿到 1750 亿不等。下表概述了各种 GPT 模型尺寸的超参数。

使用 GPT 生成文本时，用户向模型提供一个提示（prompt）。模型处理这个提示，生成第一个输出词元（Token）和两个称为 KV 缓存（KV Cache）的张量。我们称之为初始阶段（Initial Stage）。然后，模型将前一个输出词元和 KV 缓存作为输入，生成下一个输出词元和更新后的 KV 缓存。我们称之为自回归（Auto-Regression）步骤。自回归步骤不断重复，直至模型生成完整的输出。    

计算步骤, FLOP, I/O

为了增强我们对 Transformer 层的理解，我创建了一个表格，按顺序列出了计算步骤。我们可以从上到下阅读这个表格，类似于执行程序。   除了提供了计算流程和输出形状（Shape），表格还提供了每个步骤的 FLOPs（浮点操作，即计算量）和 I/O 字节数（从 GPU 内存传输到 GPU 寄存器的数据传输）的数量。当将一个 NxM 矩阵与一个 MxP 矩阵相乘以产生一个 NxP 矩阵时，FLOP 计数为 N*M*P，I/O 计数为 N*M + M*P + N*P。此外，我们定义算术强度（Arithmetic Intensity）为 FLOP : I/O。

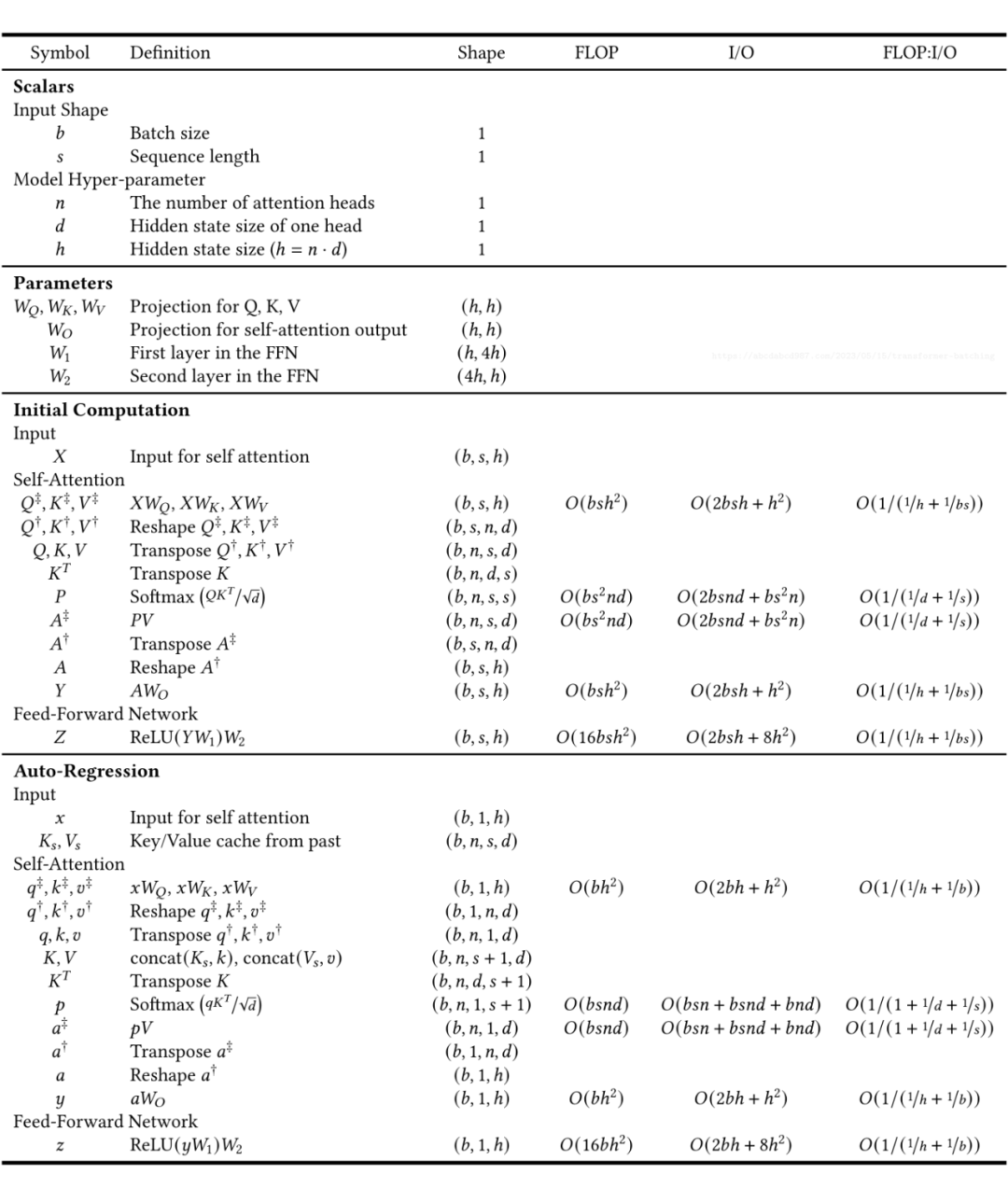
让我们一起仔细研究这张表格。以下是我觉得一些有趣的点：

参数：

自注意力具有 3h^2 个参数，而前馈神经网络（加上输出投影（Output Projection））具有 9h^2 个参数。

自注意力仅占总模型参数的四分之一。

内存使用：

Softmax（QK^T）占用的内存为 n*s^2，这是大语言模型难以支持较长的文本长度的原因之一。举个例子，67 亿参数的模型具有 32 个注意力头（Self-Attention Head），假设输入有 16384 个词元，那么我们需要 16 GB 的内存来存储这个临时值（32 * 16384^2 * sizeof（float16））。

相比之下，Softmax（QK^T）V 以及 Q，K，V 和其他隐藏状态（Hidden States）只使用 n*d*s 内存。在前面的例子中，大小为 128MB（4096 * 16384 * sizeof（float16））。

K，V 需要保存下来以供后续自回归使用。在前面的例子中，每层 KV 缓存占用 256 MB（128 MB * 2），67 亿参数的模型有有 32 个 Transformer 层，那么总的 KV 缓存需要占用 8GB（256 MB * 32）显存。

时间复杂度：

众所周知，Transformer 时间复杂度与序列长度平方成正比，正如上表中表示 Q，K，V 的矩阵乘法的行所示。

更准确地说，考虑到密集层，初始阶段的总时间复杂度为 O（s^2h + sh^2），自回归阶段为 O（sh + h^2）。

鉴于 h（>4096）通常比 s（<2048）大得多，可以说嵌入（Embedding）维度 h 的二次项比序列长度更影响时间复杂度。

矩阵乘法：

Transformer 层涉及两种类型的矩阵乘法。

第一种类型是密集层：

密集层使用向量矩阵乘法将输入向量转换为另一个向量。

对于更高维度的输入，向量矩阵乘法在除了最后一个维度之外的所有维度上进行广播。例如，当将形状为（h, h）的密集层应用于形状为（b, s, h）的张量时，在矩阵乘法之前将张量重塑（Reshape）为（b*s, h），然后在之后重塑回（b, s, h）。

对于形状为（(h, h）的密集层和形状为（b, h）的批处理输入，计算强度为 O（1 /（1+1/b））。增加批处理大小可以提高密集层的效率。 

第二种类型是自注意力：

自注意力计算一个输入序列中词元之间的关系。

对于批处理输入，Q 和 K 的形状都为（b, n, s, d）。操作 QK^T 实际上是批处理矩阵乘法（Batched Matrix Multiplication）。对于批处理的第 i 个条目和第 j 个注意力头（Self-Attention Head），结果 out[i, j] := matmul（Q[i, j, :, :], K[i, j, :, :].T）。随着 b 的增加，计算和 I/O 需求都增加，使算术强度保持不变。 

初始阶段的批处理：

密集层：

由于序列长度这一维度的存在，即使批处理大小为 1，输入也已经是批处理的。

因为序列长度通常很长，所以我们可以认为它已经很好地进行了批处理。

因此，在初始阶段，批处理对密集层的效益不大。

自注意力：

正如前面提到的，批处理不会增加自注意力的算术强度。因此，在初始阶段，批处理对自注意力并没有帮助。（其实也不完全是这样……我们会在下一个部分讨论。）

自回归阶段的批处理：

密集层：

自回归阶段的密集层输入的形状为（b, 1, h）。

显然这里批处理能带来的大幅效率提升。

自注意力：

同理，批处理在这里并没有什么作用。（其实也不完全是这样……我们会在下一个部分讨论。）

全程的批处理：

密集层和自注意力：

批处理有助于密集层，但对自注意力没有帮助。

密集层占据了模型参数的 3/4，这表明密集层的执行时间占据了整个 Transformer 层执行时间的一大部分。

因此，批处理对整个模型的效益很大。

初始阶段和自回归：

初始阶段已经在序列长度这一维度进行了很好的批处理，提升空间较小。而自回归能从批处理中获得很大的吞吐量提升。

自回归步骤通常要执行非常多次，例如生成 100 个甚至 1000 个词元。因此，自回归比初始阶段要花费更多时间。

因此，批处理能极大地提高端到端文本生成的效率。

微基准测试

我决定做一些微基准测试（Microbenchmark）来验证我对密集层、自注意力、初始阶段、以及自回归阶段中批处理效应的理解。  

测试代码大致如下：

def bench_dense(n, d, b, s):
  h = n * d
  X = torch.rand((b, s, h), dtype=torch.bfloat16, device="cuda")
  W = torch.rand((h, h), dtype=torch.bfloat16, device="cuda")
  def run():
    torch.matmul(X, W)
    torch.cuda.synchronize()
  latency = benchmark(run)

def bench_qk_init(n, d, b, s):
  Q = torch.rand((b, n, s, d), dtype=torch.bfloat16, device="cuda")
  K = torch.rand((b, n, s, d), dtype=torch.bfloat16, device="cuda")
  def run():
    torch.bmm(Q.view(b*n, s, d), K.view(b*n, s, d).transpose(1, 2))
    torch.cuda.synchronize()
  latency = benchmark(run)

def bench_qk_ar(n, d, b, s):
  Q = torch.rand((b, n, 1, d), dtype=torch.bfloat16, device="cuda")
  K = torch.rand((b, n, s, d), dtype=torch.bfloat16, device="cuda")
  def run():
    torch.bmm(Q.view(b*n, 1, d), K.view(b*n, s, d).transpose(1, 2))
    torch.cuda.synchronize()
  latency = benchmark(run)

我使用了 PyTorch 2.0，在 NVIDIA A100 上运行了这些基准测试。基准测试参数的范围是：

h = [768, 1024, 2048, 4096, 5120, 7168, 9216, 12288]
s = [1, 10, 20, 50, 100, 200, 500, 1000, 2000, 5000]
b = [1, 2, 3, 4, 5, 6, 7, 8,
     10, 12, 14, 16, 20, 24, 28, 32,
     40, 48, 56, 64, 80, 96, 112, 128]

3.1 整体批处理

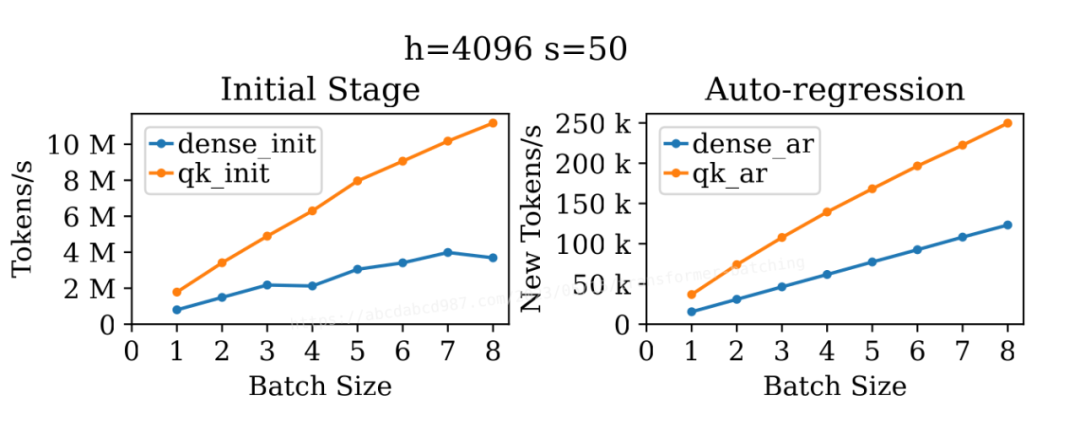
上图展示了批处理大小对密集层和自注意力在初始阶段和自回归阶段吞吐量的影响。出乎我的意料的是，这四条线都展现出了批处理对吞吐量的提升。  

对于 dense_init，批处理的提升可能是因为序列长度较小（50）。A100 轻松处理了大小为 4096 × 4096 × 4096 的矩阵乘法，而批处理大小为 50 未能充分利用所有可用的计算单元。  

那么，对于更长的序列长度呢？

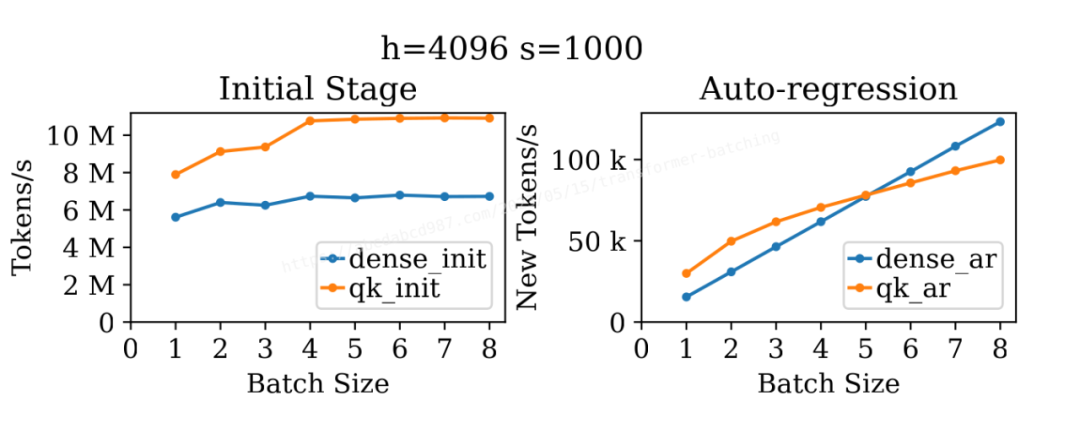
上图展示了类似的结果，但序列长度为 1000。再次出乎我的意料的是，无论是 qk_init 还是 qk_ar 都在批处理中获得了提升，尤其是在比较批处理大小为 1 和 4 时。可能的原因是，在并行运行 32*b 个这样的矩阵乘法实例时，执行 1000 × 128 × 1000 的矩阵乘法实际上太容易了。另一个解释可能是矩阵乘法核心不够优化，未能充分利用可用的计算单元。  

另一方面，由于序列长度已经很长，dense_init 不再从批处理中获得吞吐量的提升。正如先前分析的那样，在这个例子中 dense_ar 依然具有极佳的批处理效应。

3.2 密集层的批处理

让我们更仔细地看看密集层。

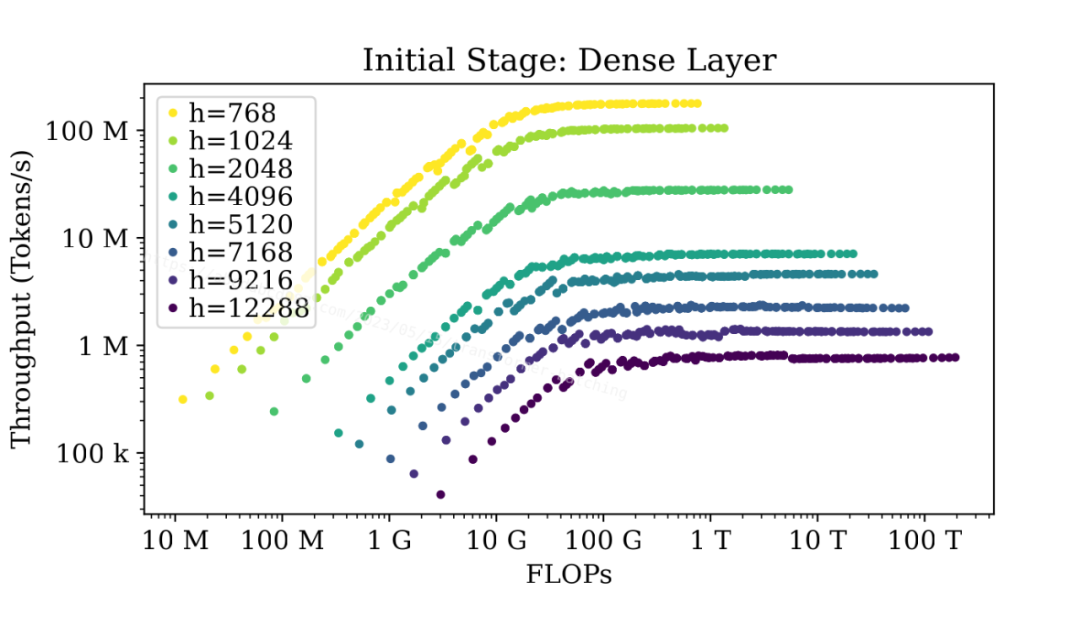
上图显示了不同大小的密集层的吞吐量与总浮点运算数（FLOPs）之间的关系。该图使用 FLOPs 作为 x 轴，基本上等同于 b*s 相似，因为 FLOPs 是 O(bsh^2)。比起使用 b*s 作为 x 轴，使用 FLOPs 作为 x 轴可以更好地在同一张图中区分不同的模型大小。  

图中显示，无论模型有多大，当序列长度不大时，密集层在初始阶段在达到最大吞吐量之前都可以在不同程度上受益于批处理。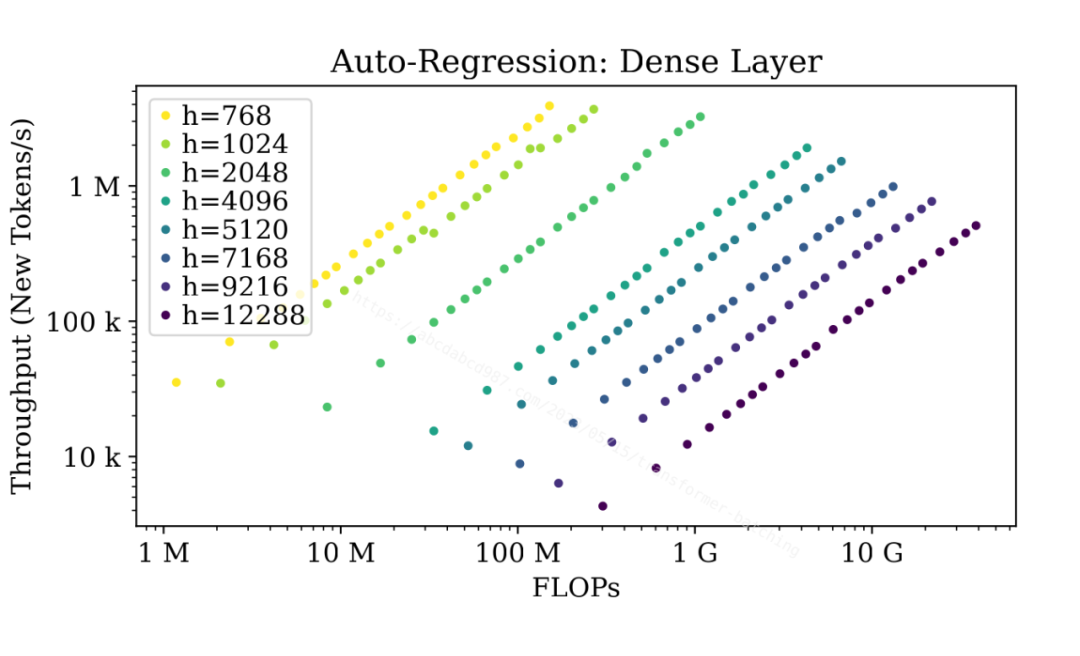



上图显示了自回归阶段。由于自回归阶段中的密集层序列长度始终为 1，批处理效应几乎没有上限。

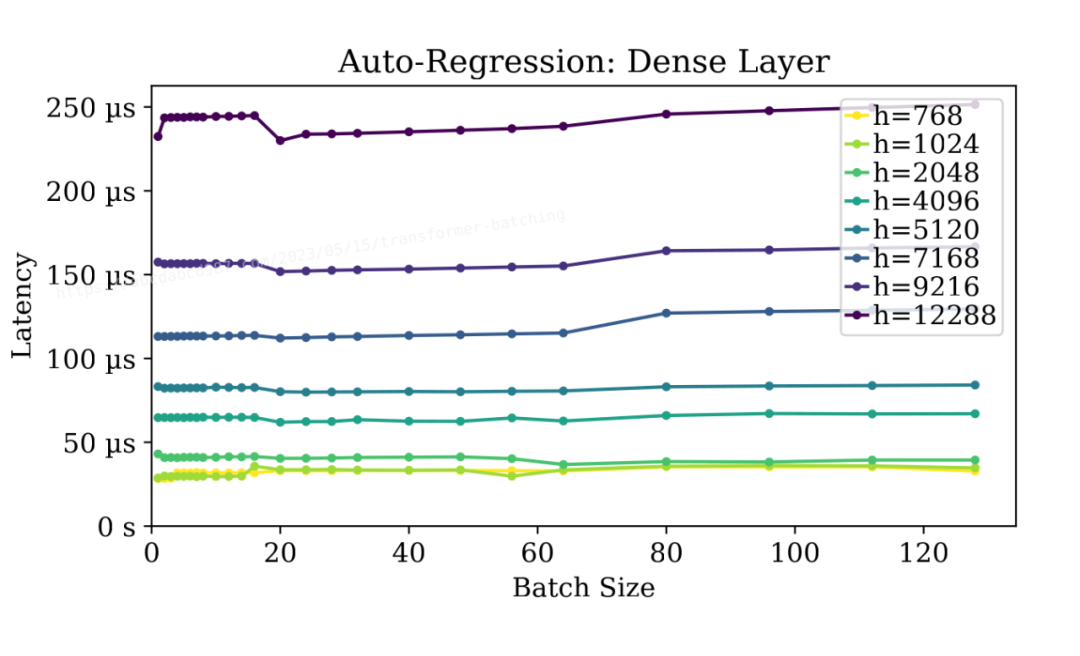
更好的是，如上图所示，批处理自回归阶段的密集层不会对延迟产生显著影响。批处理大小为128时，几乎与无批处理时的延迟相当低。这简直就是天上掉馅饼！

3.3 自注意力的批处理

现在，让我们来看看自注意力。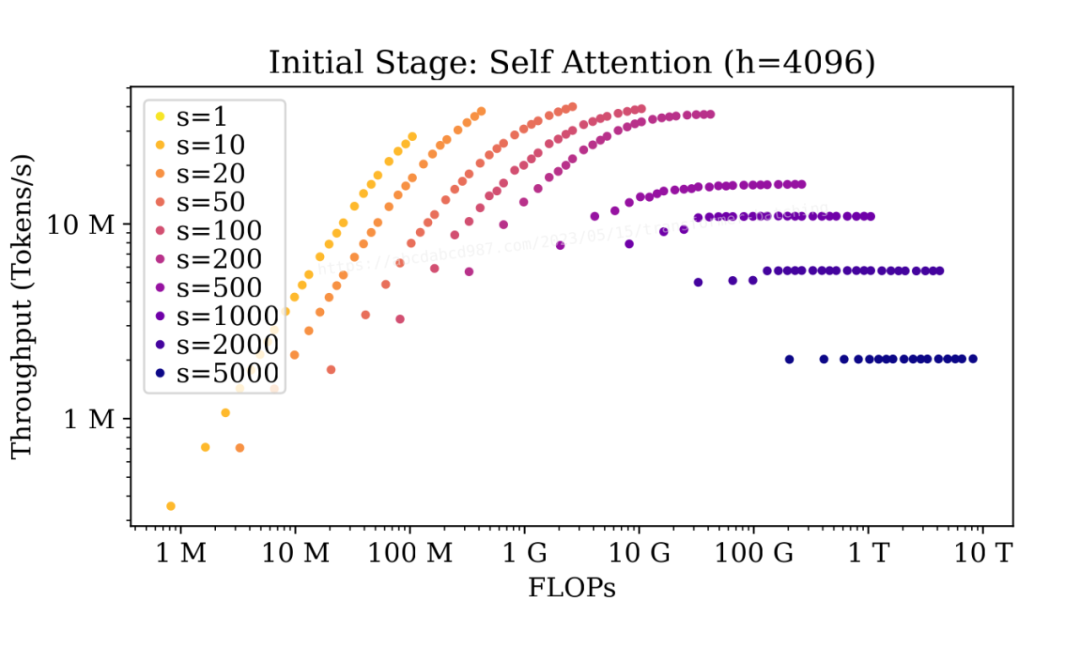



在初始阶段，当序列长度较短（s<=100）时，批处理会产生显著的影响，但对于较长的序列（s>=500），批处理的影响较小。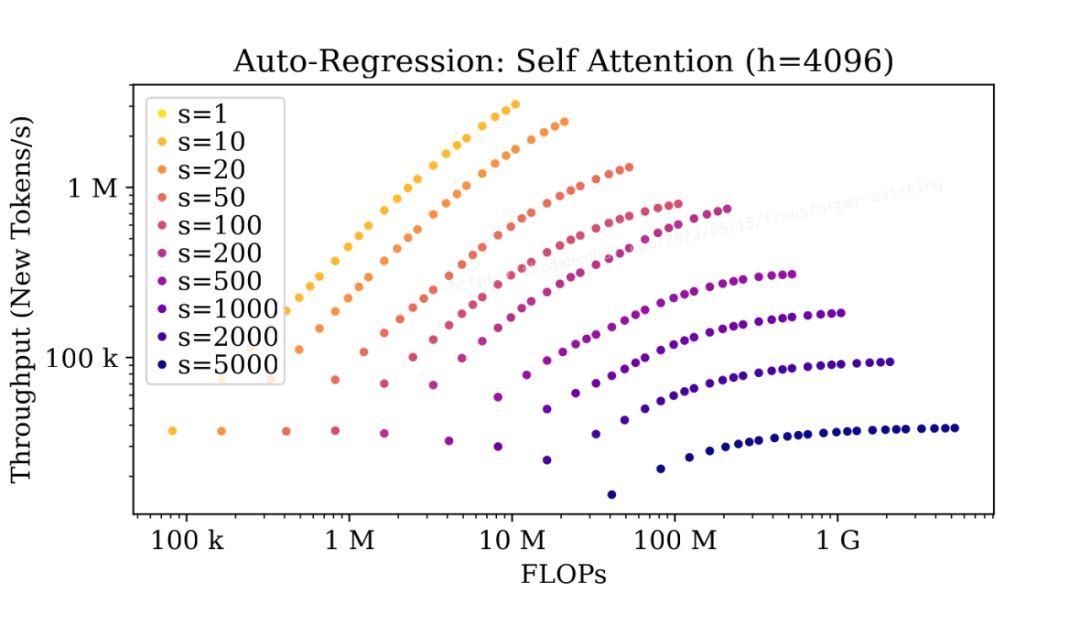



自回归阶段的情况类似，因为两个阶段中的自注意力具有相同的 FLOP:I/O 比例。要注意的是，随着自回归的进行，序列长度会逐渐增加，批处理的提升也会逐渐减少。

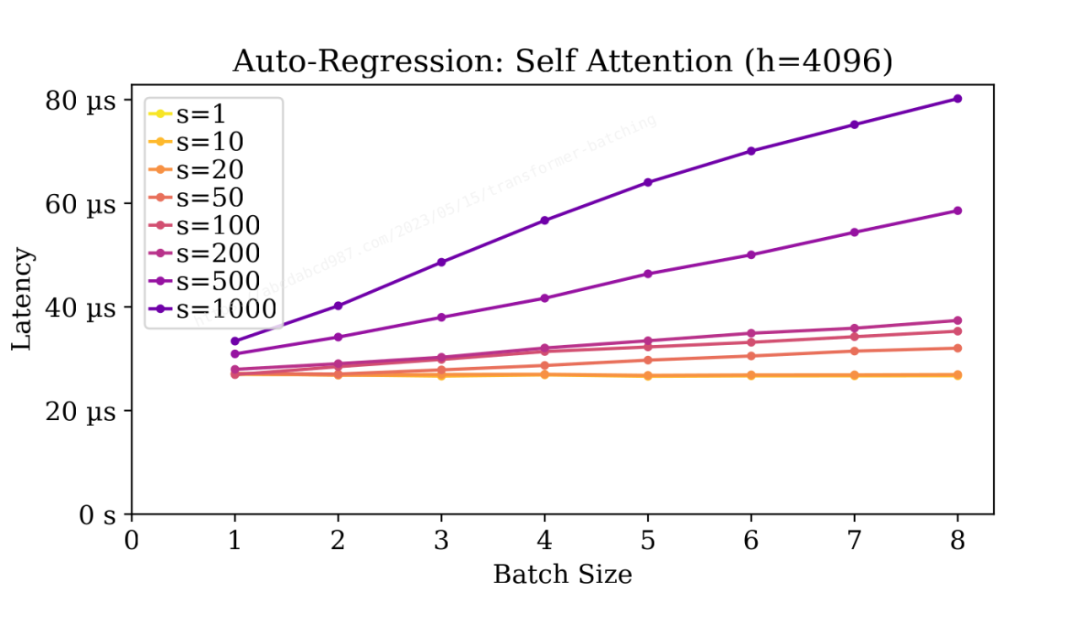
自注意力的延迟与密集层的延迟相当。

与密集层不同，自注意力的延迟随批大小增加而增加。

延迟与批大小大致呈线性关系。这是因为自注意力本质上是批量矩阵乘法。在固定的 FLOP:I/O 比例下，批处理意味着更多的工作量，但并没有在单个任务上获得速度上的提升。

同样，随着自回归的进行，序列长度逐渐增加，每个步骤的处理时间也逐渐增加。

3.4 屋顶模型

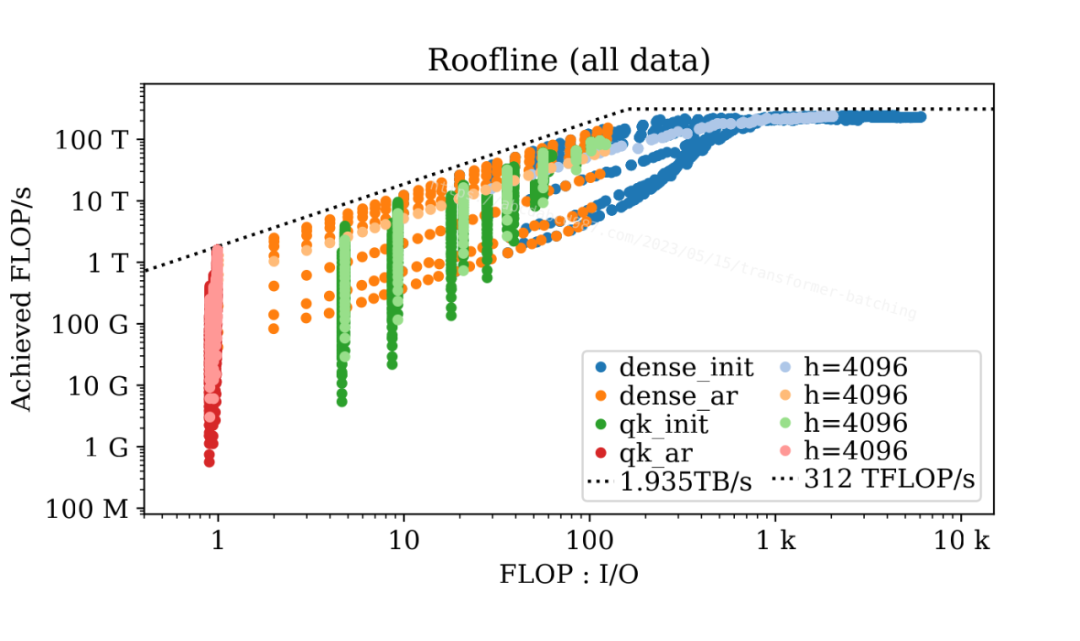
上图套用屋顶模型 [2]（Roofline Model）展示了基准测试参数的所有组合的数据点。四种颜色代表不同的阶段和层。每种颜色都包含一个较浅的版本，展示了 67 亿参数模型的数据点作为示例。此外，图中显示了来自 NVIDIA A100 参数表 [3] 的理论内存带宽和 FLOP/s。  

这张图有两个非常有趣的现象。一是数据点聚集成群和子群；二是数据点与理论屋顶线非常接近。  

为了探究批处理的影响，让我们来看一个特定的案例（h=4096, s=100）：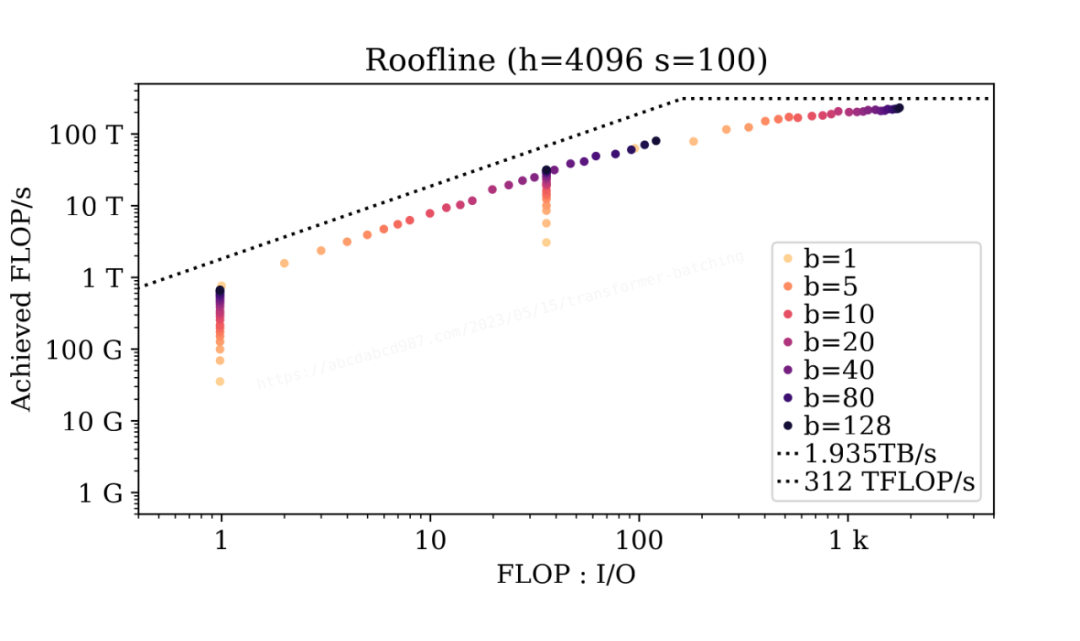

 

从这两张图中，我们可以得出以下结论：  

算术强度的顺序为：dense_init > qk_init > dense_ar > qk_ar。

效率（达成的 FLOP/s）的顺序为：dense_init > qk_init > dense_ar > qk_ar。

初始阶段的密集层受限于 GPU 的峰值计算性能。当序列长度较短且模型较小时，批处理可以提供轻微的效率提升。其余的情况，要提升初始阶段的密集层性能的唯一办法，就是加钱找老黄买更强的 GPU。

同大小的模型的自回归阶段的密集层数据点形成一条线。这条线的斜率与 GPU 的内存带宽相同。因此，自回归阶段的密集层受到内存带宽的限制。增加批大小可以提高密集层的算术强度，于是在内存带宽约束下增加实现的 FLOP/s。

批处理不会改变自注意力的算术强度。然而，在序列长度较短的情况下，批处理通过并行处理提高了自注意力的达成的 FLOP/s。在不改变算术强度的情况下达成的 FLOP/s 却增加了，这意味着自注意力的内核实现可能不够优化，没有充分利用所有计算单元。

文本生成端到端基准测试

在前面的部分，我们对密集层和自注意力进行了微基准测试。现在，让我们通过一个端到端的基准测试来研究批处理对文本生成的影响。在这个基准测试中，我使用了 67 亿参数的模型，输入词元长度为 200，输出词元长度为 500。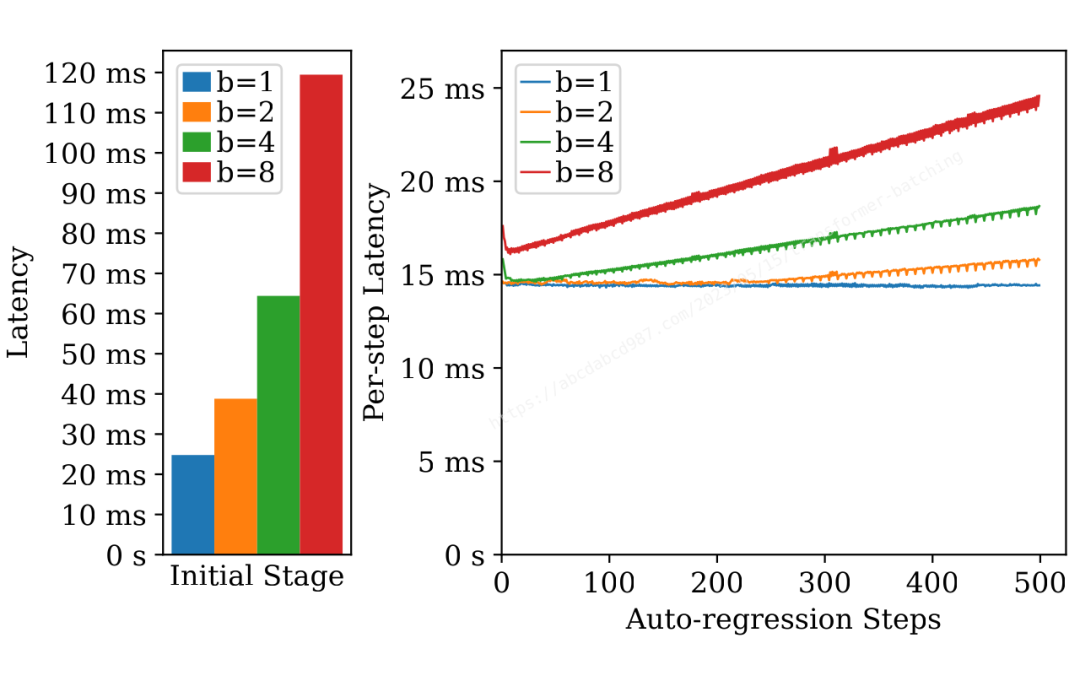

 

上面的图表显示了不同批处理大小下初始阶段和每个自回归步骤的延迟。从这个图表中可以看出一些有趣的现象：  

自回归步骤的延迟与初始阶段的延迟相当。考虑到生成数百个新词元，总延迟主要受自回归的影响。

初始阶段具有轻微的批处理效应，批处理大小为 1 时延迟为 24 毫秒，批处理大小为 8 时延迟为 119 毫秒。

自回归步骤显示出明显的批处理效应。最后一个词元（即最慢的词元）在批处理大小为 1 时需要 14 毫秒，在批处理大小为 8 时需要 24 毫秒。

根据这些观察结果，我们可以做出合理的推测：批处理可以显著提高吞吐量，而仅对延迟产生轻微影响。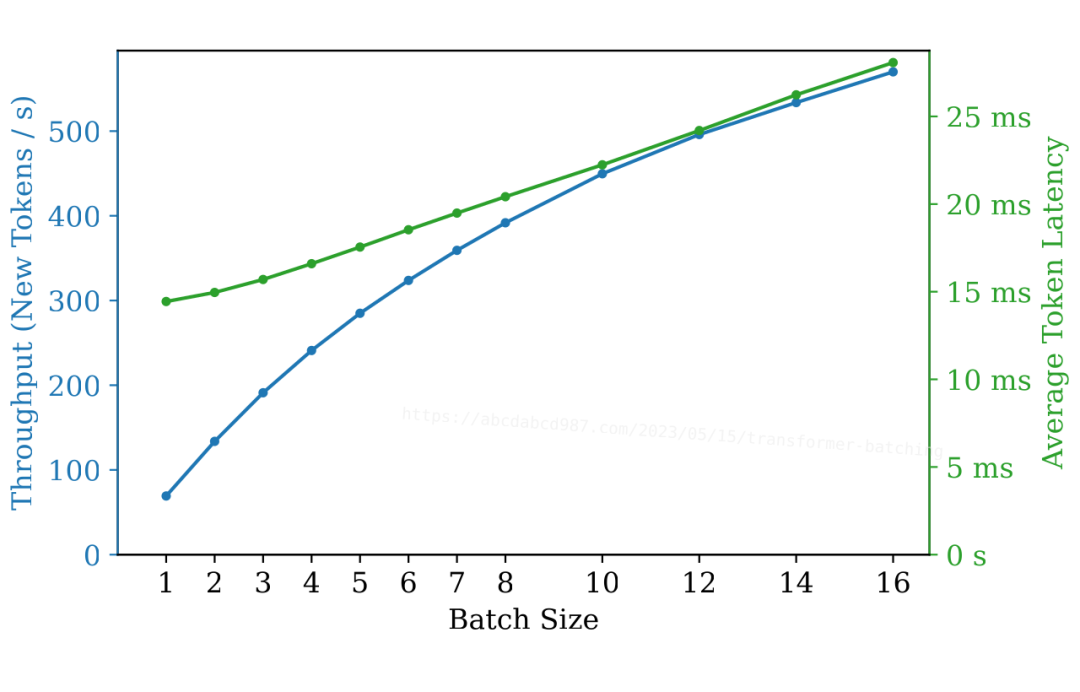

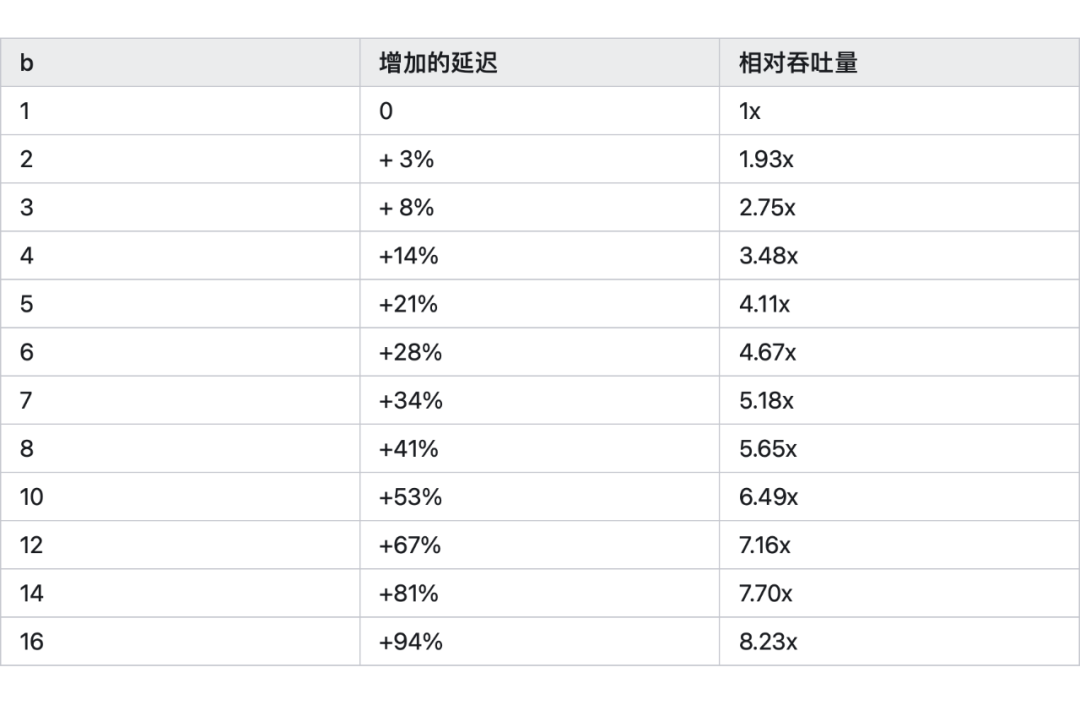
上面的图表确认了这个推测：  

在批处理大小为 2 时，延迟几乎保持不变，但吞吐量几乎增加了一倍。

在批处理大小为 4 时，延迟增加了 14%，而吞吐量是原先的 3.5 倍。

延迟与批处理大小大致呈线性关系。

我们可以这样理解：

图表中的延迟包含一个初始阶段和 500 个自回归步骤。如前所述，主要影响延迟的是自回归。因此，我们将重点放在自回归阶段。

回顾微基准测试部分的图表，我们可以观察到自注意力的延迟与批处理大小呈线性关系，而密集层的延迟几乎不受批处理大小的影响。

尽管密集层的运行时间比自注意力长几倍，但自注意力长仍然对整个层的总延迟产生显著影响。因此，延迟与批处理大小之间的线性关系延伸到整个层。

此外，随着批处理大小的增加，吞吐量的提升变少。

我们可以使用一个简单的分析模型来理解这种边际收益递减。

假设批处理大小为 b 的延迟是 c0 + c1 * b，其中 c0 和 c1 是正的常数。

批处理大小为 b 的吞吐量则是 b / (c0 + c1 * b)。

吞吐量的斜率由 c0 / (c0 + c1 * b)^2 给出，它始终为正（表示随着批处理大小的增加而提高吞吐量），但递减（意味着边际收益递减）。

批处理大小 1 和 2 之间的延迟差异显著小于较大批次之间的差距。

这是因为批处理大小为 1 时没有充分利用所有可用的计算单元。因此，当使用批处理大小为 2 运行时，我们可以获得一些额外的效率而不会产生显著地增加延迟。

提升大语言模型推断性能

在研究了大语言模型推断性能后，让我们根据我们的发现来做点改进。

5.1 融合自注意力的计算

正如我们之前分析的那样，QK^T 生成了一个形状为（b, n, s, s）的临时输出，而我们只需要 Softmax(QK^T)V 的最终结果，其形状为（b, n, s, d）。由于 d=128 相对较小，我们可以将这三个矩阵的乘法融合成一个单独的 Cuda 核 (Kernel) 函数，直接产生 (QK^T)V。  

然而，有一个障碍：Softmax。传统的 Softmax 实现需要读取 QK^T 的最后一个维度中的所有数字。这会带来一个问题，因为我们在融合 V 的乘法时只能计算一小块 QK^T。为了克服这个限制，我们需要找到一种聪明的方式来计算 Softmax，确保它保持结合性。

幸运的是，一些聪明的人已经发现了实现在线 Softmax [4] 的方法。我们可以尝试实现这个技巧并解决一些必要的细节问题。   恭喜你！我们实质上一起重新发明了 FlashAttention [NeurIPS'22] [5] 论文。此外，我推荐阅读这篇关于 FlashAttention 的精彩笔记 [6]。

5.2 批处理请求

另一个重要的机会在于将请求进行批处理，从而在略微增加延迟的情况下，大幅增加吞吐量，正如我们之前讨论的那样。大语言推断服务，如 OpenAI ChatGPT [7] 和 HuggingFace Hosted Inference [8]，可以从批处理中获得极大的好处。  

在我们之前的分析中，我们做了一个简化的假设，即所有请求序列具有相同的长度。然而，在现实中，请求序列的长度是不同的。虽然将所有序列填充到相同的长度是一个选项，但它也会增加计算量。幸运的是，重新审视我们之前的发现，我们可以设计一种更简单高效的解决方案：  

给定形状为 [(s1, h), (s2, h), ...] 的输入，我们将它们堆叠成一个形状为 (sum(si), h) 的大矩阵。

对这个堆叠矩阵应用密集层。

将密集层的结果分割回 [(s1, h), (s2, h), ...]。

对每个序列进行自注意力计算。

恭喜你！我们实质上一起重新发明了 Orca [OSDI'22] [9] 论文。    

总结

我们将 Transformer 块的计算步骤、FLOPs、I/O和算术强度浓缩到了一张表格中。

我们考虑了初始阶段和自回归阶段，分析了对密集层和自注意力进行批处理的效果。

为了验证我们的分析，我们进行了微基准测试，并使用屋顶模型解释了结果。

我们对文本生成进行了端到端基准测试，证明批处理显著提高了吞吐量，而只增加了微小的延迟。

我们通过融合自注意力的计算，以及支持跨请求批处理，来改进了大语言模型推断系统。

审核编辑：刘清