相机标定中的坐标变换原理难点分析

小伙伴们大家好！相信有一些同学在接触到标定的时候被花式坐标系转换、矩阵公式、畸变搞得一头雾水，今天我就带大家直击原理难点，一举拿下手眼标定！   如果有小伙伴进行过标定的操作，一定还记得其中有一句话—“进行手眼标定前一定要先进行相机标定”。这是因为相机标定的目的主要是为了获得相机的内参矩阵以及畸变系数，手眼标定的计算过程中需要用到这些参数。  

相机标定中的基本坐标系有：像素坐标系、图像坐标系、相机坐标系、世界坐标系，这些坐标系之间都有一定的转换关系，若这些转换关系已知，就可以得到世界坐标（棋盘上的点）和像素坐标之间的关系。在不考虑相机的畸变而只考虑空间坐标转换的情况下，像素坐标=内参矩阵*外参矩阵*世界坐标。这就有了后面的坐标系之间的转换关系的求解。  

图像坐标系（x,y）到像素坐标系（u,v）

像素坐标就是像素在图像中的位置，一般像素坐标系左上角的顶点就是原点，水平向右是u轴，垂直向下是v轴。在像素坐标系中，每个像素的坐标是用像素来表示的，然而，像素的表示方法却不能反映图像中物体的物理尺寸，因此，要将像素坐标转换为图像坐标。   将像素坐标系的原点平移到图像的中心，定为图像坐标系的原点。  

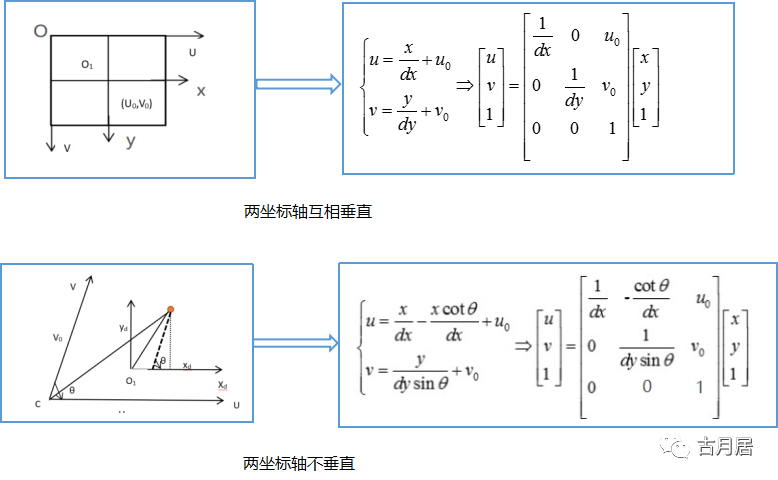
无论两坐标轴垂直与否，我们可以记为  

注：此处写成齐次是为了后面计算方便，下同。    

相机坐标系（Xc,Yc,Zc）到图像坐标系(X,Y)

相机成像原理是小孔成像，即简单的相似原理。根据小孔成像原理，同时为了方便计算，投影到同一侧，其中OCXCYCZC是相机坐标系，OiXY是图像坐标系。如下图，由▲ABOC~▲CPOC和▲AOCD~▲COCOi 可得  

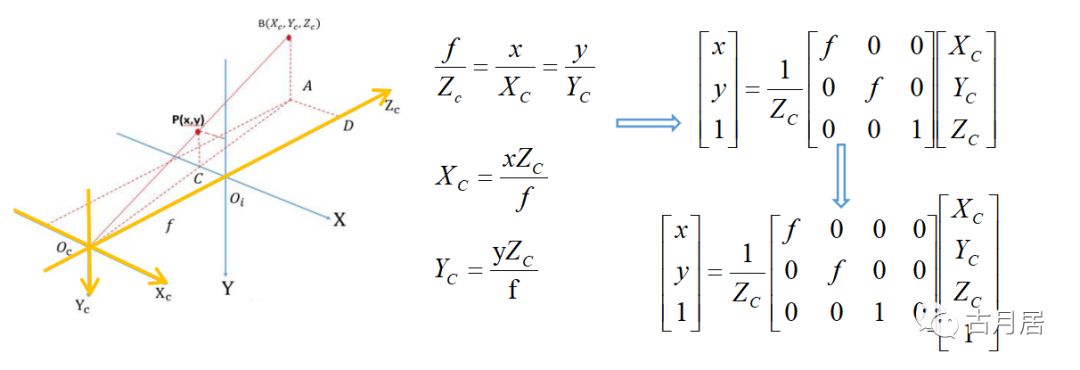
世界坐标系（Xw,Yw,Zw）到相机坐标系（Xc,Yc,Zc）

单纯的刚体变换，只涉及到旋转和平移，其中R3x3是旋转矩阵，T3x1是平移向量。  

好了，准备工作做好了，我们来看看吧！  

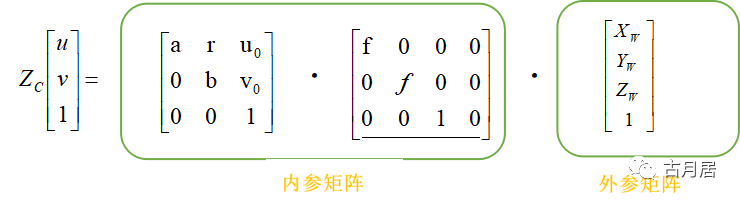
内参矩阵只与相机本身有关。   当然，我们前面已经说了这是理想的情况，实际情况中，受透镜和安装的影响，会产生畸变，主要为径向畸变和切向畸变。图像径向畸变是图像像素点以畸变中心为中心点,沿着径向产生的位置偏差,从而导致图像中所成的像发生形变。径向畸变是因为离图像中心，光线越弯曲造成的，主要有枕形畸变（图1左）和桶形畸变（图1右）。图像径向畸变是成像过程中最主要的畸变,同时也是对成像效果影响最大的畸变；切向畸变是因为透镜在安装的过程中，与成像平面不平行造成的。  

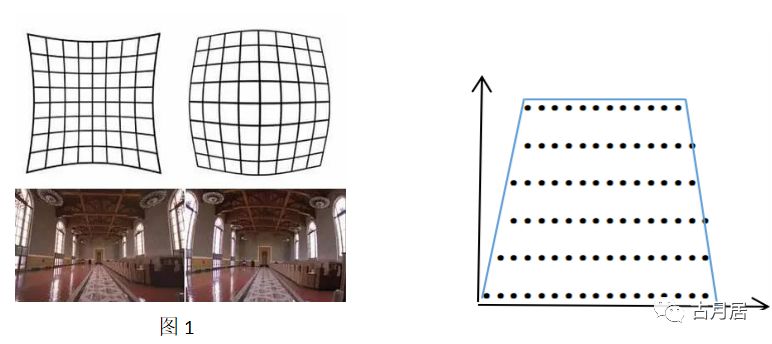
对于径向畸变，光学中心的畸变为0，随着向边缘移动，畸变越来越严重。   对于径向畸变可以通过下面的泰勒级数展开式进行校正：  

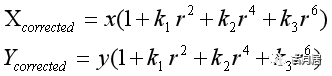
这里的x、y是图像中的畸变后的位置坐标，通过校正得到真实坐标。r是该点距成像中心的距离。   切向畸变可以通过以下公式来矫正：  

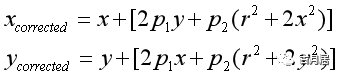
所以标定获得的畸变参数也就是[k1,k2,k3,p1,p2]。   在这里，我认为理想情况下的推理帮助我们清理头绪，而考虑畸变之后的复杂运算，我们理论上看懂即可，实际标定中复杂的计算，大可交给我们的计算机。   我们再回到手眼标定上来。手眼标定分为:eye-in-hand (眼在手上) 、eye-on-hand(眼在手外)。网上有不少以眼在手外为例的资料可供参考，这里我就以眼在手上为例。手眼标定的求解从本质上来说就是来解出方程AX=XB中的矩阵X，其中X即为对应相机坐标系到机械臂末端坐标系的转换矩阵，通常所说的对应“眼”到“手”的关系。  

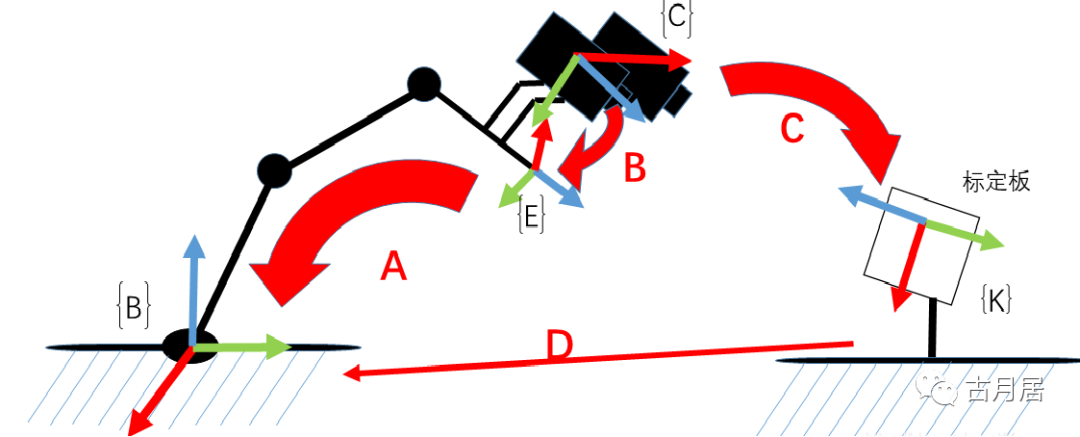
上图清楚地标明了各个坐标系之间的关系:   A:机器人末端在机械臂坐标系下的位姿，即机器人运动学正解的问题(已知) B:相机在机器人末端坐标系下的位姿，固定(未知，待求) C:相机在标定板坐标系下的位姿，即求解相机的外参(已知) D:我怎么知道。。。待求   只要我们能计算得到B变换，那么相机在机器人坐标系下的位姿D也就自然得到了。   参看下图，可得C1-1BA1=C2-1BA2,整理一下有 --> C2C1-1B=BA2A1-1,这是典型的“AX=XB”问题。  

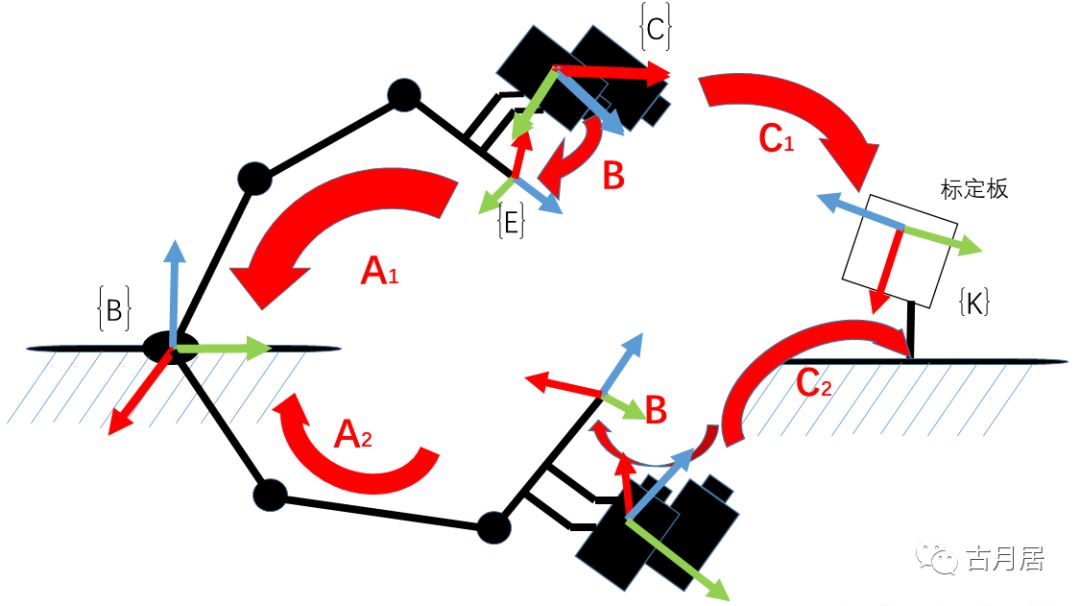
前面图文并茂略显粗糙的概述，主要是为了理清思路，对于每个部分的细节都给省略掉了，接下来对A、C进行说明。   变换A: 它是机械臂末端在机器人基座坐标系下的位姿，其实就是机器人学里面最基础的运动学正解。如下图  

变换C：相机在标定板坐标系下的位姿，即相机的外参。其中的R,T 即为相机在标定板下的位姿。在相机标定过程中已经求得，求取步骤可以用张正友相机标定的方法。   AX=XB问题：手眼标定的四种经典算法：   (1)通过几何关系求解---------Tsai-Lenz算法 (2)通过欧几里得群求解-------Navy算法 (3)通过单位四元数求解-------Horaud算法 (4)通过对偶四元数求解-------Dual quaternions算法   其中最常用的是Tsai-Lenz算法。大家可以自行搜索求解方法。  

审核编辑：黄飞