OpenCV边缘检测算子Laplace、LoG详解

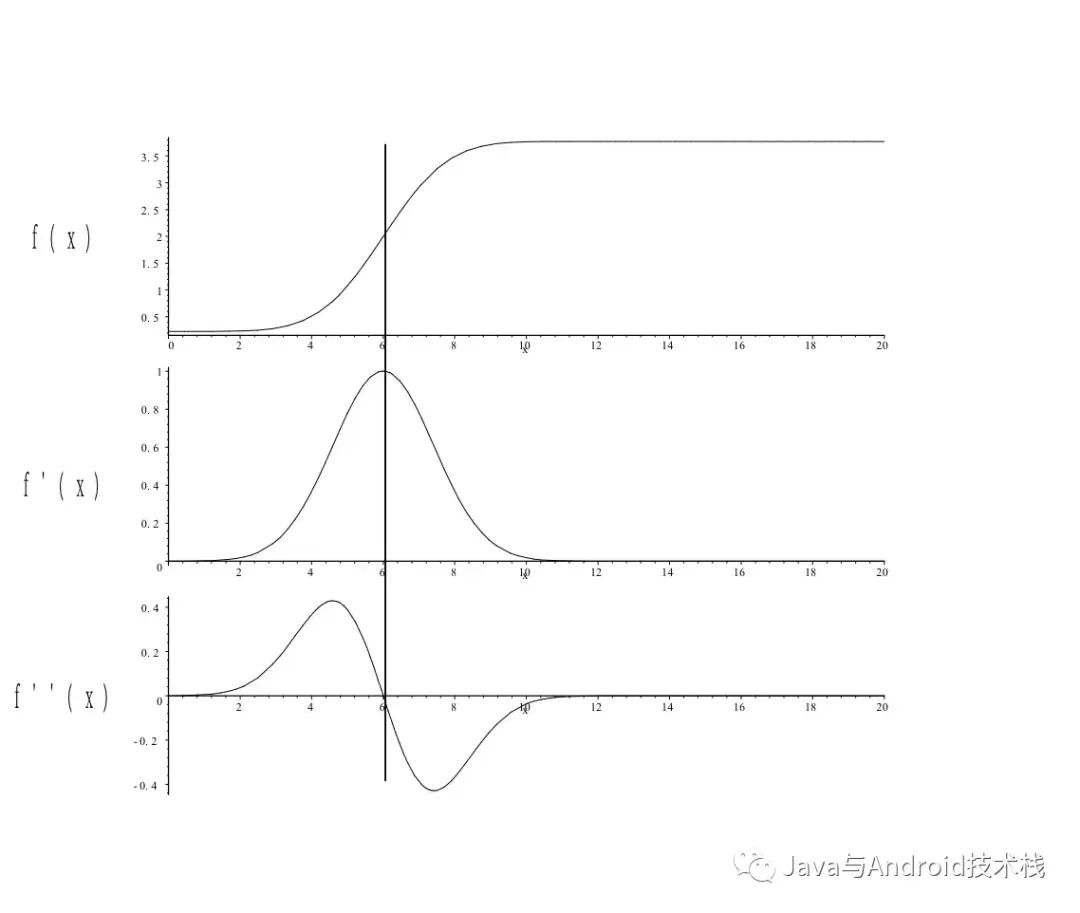
在该系列的第八篇文章中，我们曾介绍过一阶导数和二阶导数对分析边缘的结论：

一阶导数通常在图像中产生较粗的边缘；

二阶导数对精细细节，如细线、孤立点和噪声有较强的响应；

二阶导数在灰度斜坡和灰度台阶过渡处会产生双边缘响应；

二阶导数的符号可用于确定边缘的过渡是从亮到暗还是从暗到亮。

一阶导数算子(例如 Sobel 算子)通过对图像求导来确定图像的边缘，数值绝对值较高的点对应了图像的边缘。如果继续求二阶导，原先数值绝对值较高的点对应了过零点。因此，也可以通过找到二阶导数的过零点来检测边缘。在某些情况下，找二阶导数的过零点可能更容易。

一阶导数和二阶导数.png

Part11.  Laplace 算子

之前我们曾介绍过二阶导数的 Laplace 算子可以通过差分近似来简化，其公式为

它的卷积核：

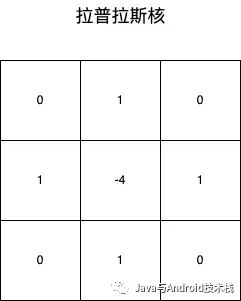
拉普拉斯核.png

这是它的 4 邻域卷积核。

11.1 Laplace 算子的扩展

Laplace 算子是具有旋转不变性的各向同性的算子。

将 4 邻域的 Laplace 算子旋转 45° 后，与原算子相加，就可以得到 8 邻域的算子。

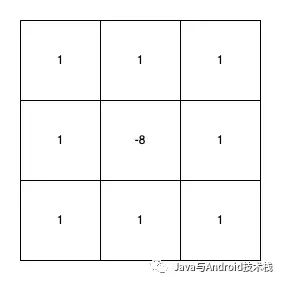
扩展的拉普拉斯算子.png

这是它的 8 邻域卷积核。这个算子表示一个像素周围一圈 8 个像素的和与中间像素 8 倍的差，作为拉普拉斯计算结果。

另外，还有两个拉普拉斯卷积核，分别是对 4 邻域卷积核和 8 邻域卷积核取反。

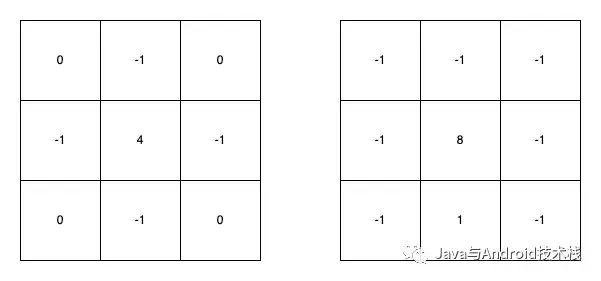
扩展的拉普拉斯算子2.png

21.2 图像的模糊检测

使用拉普拉斯变换对图像进行模糊检测的步骤大致如下：

对图像进行拉普拉斯变换，检测水平和垂直边缘

然后对拉普拉斯变换后输出的图像求方差

如果图像足够清晰，输出图像的方差会大于给定阈值

如果图像相对模糊，则拉普拉斯变换在图像中并不能检测到足够的细节，边缘就越少，从而导致输出图像的方差小于给定阈值

该过程需要选择合适的阈值。

拉普拉斯算子能突出显示图像中包含快速梯度变化的区域，这些区域往往与边缘有关。因此，如果一幅图像的方差较高，说明图像中存在广泛的边缘响应，包括类边和非类边，这是一幅正常聚焦图像的代表。但如果方差很低，那么表明图像中的边缘响应很小，几乎没有边缘存在。因此，通过比较方差与预设阈值的大小，可以判断图像是否模糊。

按照上面的步骤实现了一个模糊检测的函数：

 

bool isImageBlurry(const char* inputFile, double threshold)
{
    Mat src = imread(inputFile);
    if (src.empty()) {
        printf("Image not loaded
");
        return false;
    }

    Mat gray;
    cvtColor(src, gray, COLOR_BGR2GRAY);
    Mat dst, absDst;
    cv::Laplacian(gray, dst, CV_16S, 3);
    cv::convertScaleAbs(dst, absDst);

    Mat mean, stddev;
    double m = 0, sd = 0;
    meanStdDev(absDst, mean, stddev);
    m = mean.at(0, 0);
    sd = stddev.at(0, 0);
    double result = sd * sd;
    std::cout << "m: " << m << std::endl;
    std::cout << "StdDev: " << result << std::endl;
    return result <= threshold;
}

 

然后写一个程序来判断一下这张图是否是模糊的

 

模糊的手机图片.jpeg

 

int main(int argc,char *argv[])
{
    string fileName = ".../test.jpeg";
    bool result = isImageBlurry(fileName.c_str(),11.0);
    cout << "result =" << result <

	 

	输出结果：

	 
m: 2.5213
StdDev: 6.31374
result = 1


	 

	说明是模糊的图片。

	Laplace 算子对噪声敏感，通常不适用于存在噪声的图像。

	Part22.  LoG 算子

	LoG(Laplacian of Gaussian)边缘检测算子是 David Courtnay Marr 和 Ellen Hildreth 在 1980 年共同提出的，也称为 Marr-Hildreth 算子，它根据图像的信噪比来求检测边缘的最优滤波器。该算法先对图像进行高斯平滑处理，然后再与 Laplacian 算子进行卷积。稍后来解释为何是这样的。

	先来回顾一下二维高斯函数的公式：

	

	高斯函数的一阶导数和二阶导数，在很多算子中都会用到。例如一阶导数应用在 Canny 算子，二阶导数应用在 LoG 算子等等。

	简单推导一下它的一阶导数：

	

	同理：

	

	还有推导一下它的二阶导数：

	

	同理：

	

	将高斯函数代入拉普拉斯算子，可得 LoG 算子：

	

	Marr-Hildreth 算法如下：

	首先让 LoG 核与一幅输入图像卷积：

	

	寻找 g(x,y) 的过零点来确定 f(x,y) 的边缘位置。因为拉普拉斯变换和卷积都是线性运算，因此上式可以改成

	

	其中，f(x,y) 是输入图像，g(x,y) 是输出图像。

	这样正好解释了之前说的，该算法先对图像进行高斯平滑处理，然后再与 Laplacian 算子进行卷积。因为先使用高斯滤波器对图像进行平滑处理，可以减少噪声和细节，然后使用拉普拉斯算子对滤波后的图像进行边缘检测。

	它的优点是可以有效去除噪声，同时保留图像中的真实边缘。相比 Laplace 算子，LoG 算子具有更好的边缘定位能力和抗噪声。但是它也存在一些缺点，计算量相对较大。

	下图是负 LoG 算子的三维图像，看上去很像“墨西哥草帽”。所以，在业界也被称为墨西哥草帽小波(Mexican hat wavelet)。

	

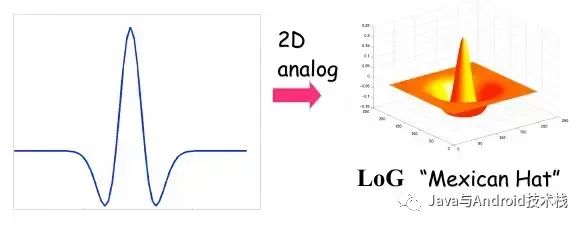
	负 LoG 算子的三维图像.png

	 

	Mexican Hat.jpg

	负 LoG 算子可用 5*5 的模版近似表示

	

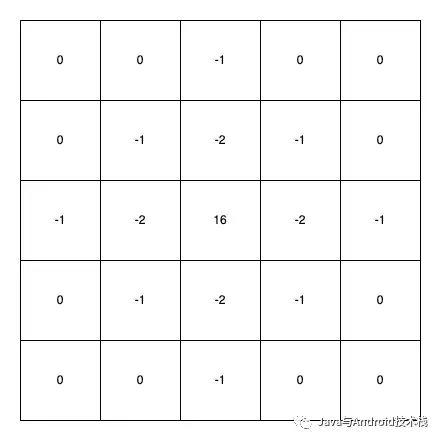
	LoG卷积核.png

	下面用高斯模糊和拉普拉斯变换来实现 LoG ：

	 
int main(int argc,char *argv[])
{
    Mat src = imread(".../street.jpg");
    imshow("src",src);

    Mat dst, gray, edge;
    cv::GaussianBlur(src, dst, cv::Size(3, 3), 0 ,0); // 高斯模糊 去除噪声
    cv::cvtColor(dst, gray, cv::COLOR_BGR2GRAY); // 灰度化
    cv::Laplacian(gray, edge, CV_16S, 3); // 使用拉普拉斯算子提取边缘
    cv::convertScaleAbs(edge, edge);

    imshow("LoG", edge);

    waitKey(0);
    return 0;
}


	 

	 

	Part33.  总结

	本文介绍了 Laplace 算子、LoG 算子，它们都是二阶导数的边缘算子。

	特别是 LoG 算子在 Laplace 算子的基础上引入了高斯滤波，可以在一定程度上克服噪声的影响。但它仍旧有一定的局限性，不过这种思想的引入对后续图像特征研究起到了积极作用，被很多后续的算法所采纳。

	 

	　　审核编辑：汤梓红