晶体知识—位错的应力场介绍

位错的应力场和应变力

位错在晶体中的存在，使其周围原子偏离平衡位置，而导致点阵畸变和弹性应力场的产生。

要进一步了解位错的性质，就须讨论位错的弹性应力场，由此可推算出位错所具有的能量、位错的作用力、位错与晶体其他缺陷间交互作用等问题。

位错的应力场

位错周围的弹性应力场弹性体假设模型：

⑴晶体是完全弹性体；

⑵晶体是各向同性的；

⑶晶体中没有空隙，由连续介质组成。

01

刃型位错的应力场

建立如图1所示的刃型位错力学模型。该模型中圆筒的轴线对应刃位错的位错线，圆筒的空心部分相当于位错的中心区。

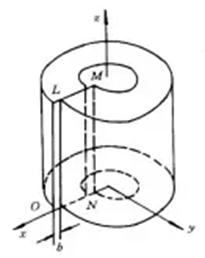
图1 刃型位错应力场

下面给出刃位错的应力场公式：

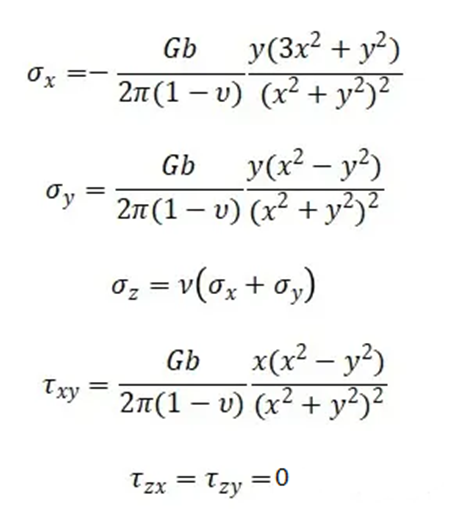
由上面所得结论可以看出：

σx与σy的符号相反。在滑移面上方，y>0，

σx为负（压应力）；在滑移面下方，y<0，

σx为正（拉应力）。

②在y＝0处有

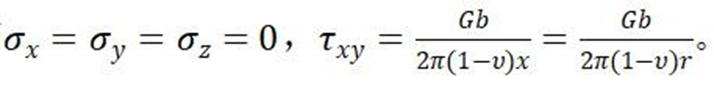
02

螺型位错的应力场

建立如图2所示的螺型位错力学模型。从该模型可知，形成螺位错时只有轴向位移，没有径向和切向位移。

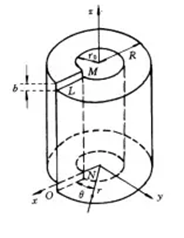
图2 螺型位错应力场

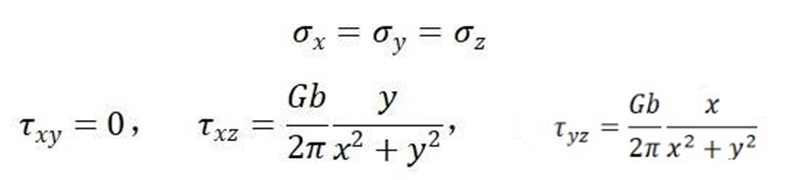
由上面的结果可知，螺位错的应力场没有正应力分量，且剪应力对称分布，在包含位错线的任何晶向平面上剪应力都是Gb/2πr，与θ角无关。螺位错不引起晶体的膨胀或收缩。

所以，无论是刃型位错还是螺型位错，作用在滑移面上的沿滑移方向的剪应力都可以写成是：

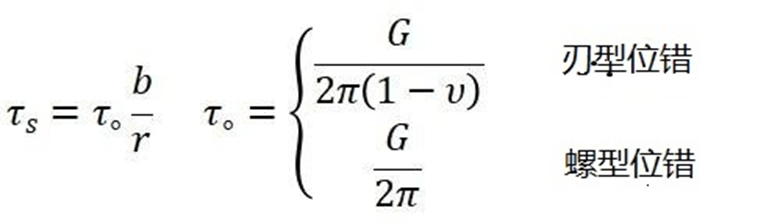
位错的应变力

位错周围点阵畸变引起弹性应力场导致晶体能量的增加，这部分能量即为位错的应变能。包括两部分：Wtot=Wcore+Wel。

（1）位错核心能Wcore：在位错核心几个原子间距ro=2|b|=2b以内的区域，滑移面两侧原子间的错排能即相当于位错核心能。错排能约占位错能的1/10，可忽略。

（2）弹性应变能Wel：在位错核心区以外，长程应力场作用范围所具有的能量，约占位错能的9/10。

由于位错在运动或与其他缺陷交互作用时，只有弹性能发生变化，因此，我们只关心各类型位错的弹性能。

刃型位错的弹性能

下面使用做功法计算刃型位错的弹性能。

首先构造一个刃位错的圆筒模型，如图3所示。

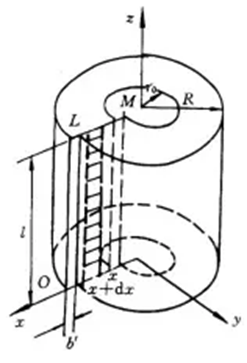
图3 刃型位错的圆筒模型

假设在形成刃位错过程中的某一时刻滑移面两边的相互位移为b´，0 < b´ < b。此时滑移面上x处产生的剪应力为：τxy=τob´/x

此后，使滑移面两边的晶体相对位移由b´增至b´+db´，则此过程中外力反抗τxy

做功为：

对上式积分可得形成伯氏矢量为b的刃型位错过程中外力所做的总功，也既是位错的弹性能为：

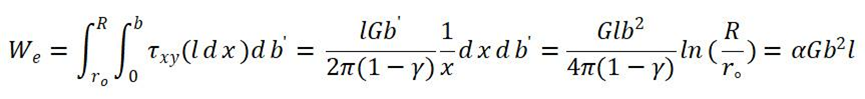
螺型位错的弹性能

采用与上面完全相同的做功法可以得到螺型位错的弹性能：

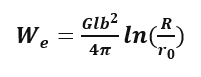
混合位错的弹性能

混合位错的弹性能应该等于其螺型分量的弹性能和刃型分量的弹性能之和。因此，对混合位错做相应分解，可以计算出混合位错的弹性能为：

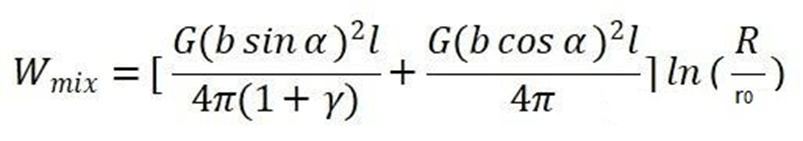
总之：

（1）位错的弹性应变能Wel ∝ lnR，即随R缓慢地增加，所以位错具有长程应力场。

（2）位错的能量是以单位长度的能量来定义的，直线位错更稳定，位错线有尽量变直和缩短其长度的趋势。

（3）位错的应变能与b2成正比。位错的弹性应变能可进一步简化为一个简单的函数式：W=aGb2。

式中W为单位长度位错线的弹性应变能，G是剪切模量，b是伯氏矢量，α=1/4πlnR/r0 其中R是晶体的外径、r0是位错核心的半径，系数a由位错的类型、密度（R值）决定，其值的范围为0.5-1.0。

意义：上式表明W ∝ b2，故可用伯氏矢量的大小来判断晶体哪些地方最容易形成位错。

 




审核编辑：刘清