应用卫星通信领域的一个坐标转换过程—机体坐标系与ENU坐标系的转换

今天我们要讲的是应用于卫星通信领域的一个坐标转换过程——机体坐标系与ENU坐标系的转换。小D将以《机载卫星通信天线角度的计算推导》为基础，来分析和推导坐标转换公式。

开头部分，我们先讲一下ENU坐标系和机体坐标系的定义。

ENU坐标系（导航坐标系）

ENU坐标系中的E表示East，N表示North，U表示Up，翻译过来就是东北天坐标系，小D第一次看到东北天这个名字时，还以为这个坐标系跟咱们祖国大东北有啥关系，后来发现没有关系。

所以，为了不让别人产生误解，小D就叫的北天东，其他文献中也有叫北东天的。另外还有一个坐标系是END，D表示Down。

ENU坐标系是以某个点为原点，三个轴表示出正东方向，正北方向和指向天上的方向，其中的“指向天上”是指垂直于水平面或海平面向上。

在大多数的文献中，ENU坐标系Z轴一般表示指向天，如果X轴指向正东方向，Y轴指向正北方向，那么这个坐标系就是ENU右手坐标系；如果Z轴指向天，X轴指向正北，Y轴指向正东，那么这个ENU坐标系就是左手坐标系。

我们今天参考的文献《机载卫星通信天线角度的计算推导》中的NEU坐标系是一个左手坐标系，并且ENU坐标系在这篇文献中也被称为导航坐标系，记作n系。ENU左手坐标系示意图如下图所示：

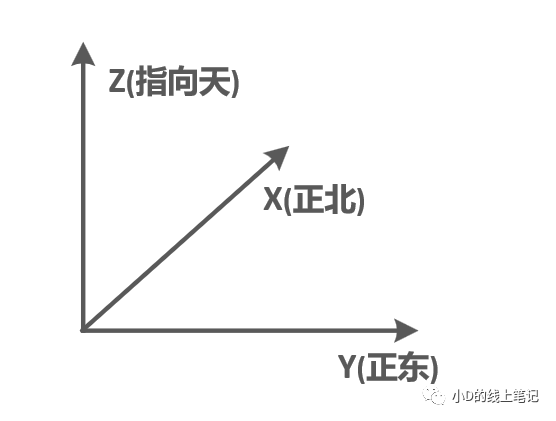
图1 ENU左手坐标系（导航坐标系n系）

机体坐标系（载体坐标系）

机体坐标系也叫载体坐标系，记作b系。机体坐标系也有很多种定义方式，有的地方定义的是左手坐标系，有的地方是右手坐标系；有的机体Z轴垂直于水平面向上，有的垂直于水平面向下。

我们今天讲的机体坐标系是这样定义的：X轴正方向指向飞机前进的方向，与机身纵轴重合，Y轴指向机身右翼，Z轴垂直于机身平面向上，构成左手坐标系。

航向角、俯仰角、横滚角

机体坐标系中有个重要的概念，就是机体姿态角，姿态角包含三个角度：航向角(yaw)，俯仰角(pitch)，横滚角(roll)，这三个角的定义如下：

航向角α：机头方向在水平面的投影与正北之间的夹角，北偏东为正，范围为0-360°；也可定义右偏为正，左偏为负，范围为-180-180°。

俯仰角β：机头方向与水平面的夹角，抬头为正，范围为-90-90°。

横滚角γ：机体绕机体纵轴旋转过的角度，右滚为正，范围为-180-180°。

其实上面各个角度都是人为定义的，你也可以有不同的定义方式，重要的是在解算角度的时候，实际的偏离角度要和定义的角度一致。

机体坐标系的航向角、俯仰角和横滚角示意图如下所示：

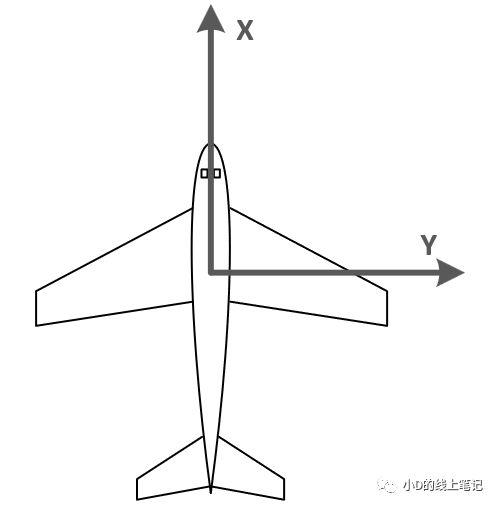
图2 飞机水平飞行时的机体俯视图

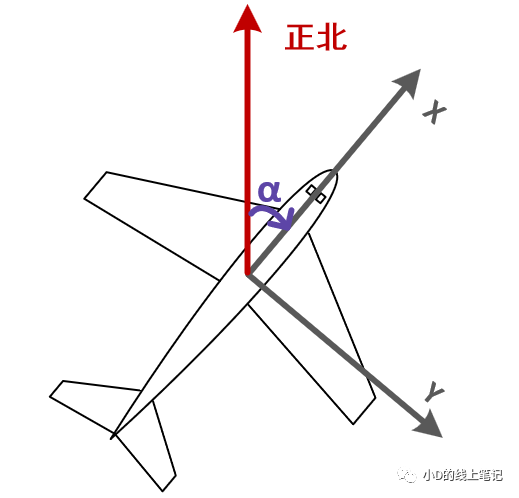
图3 机体右偏时的航向角(俯视图)

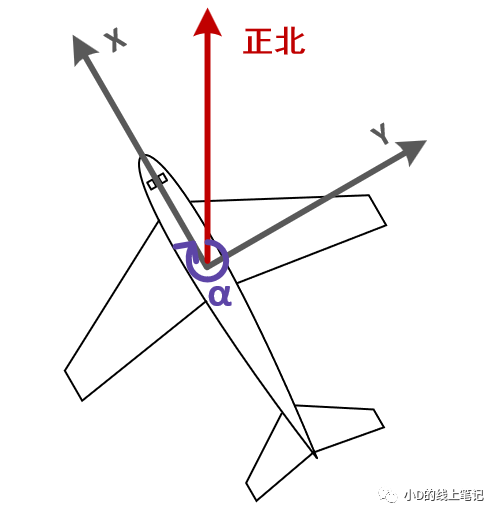
图4 机体左偏时的航向角(俯视图)

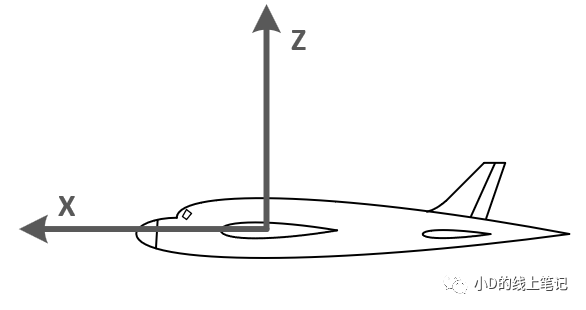
图5 飞机水平飞行时的机体左视图

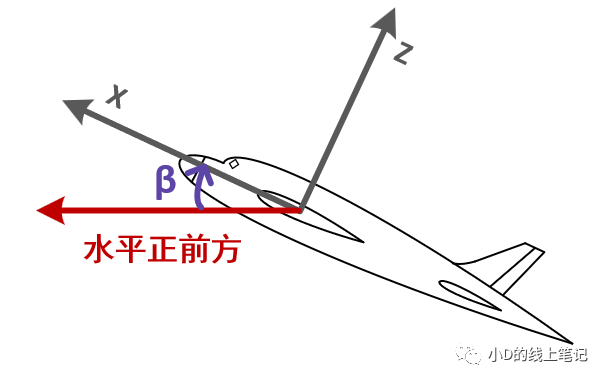
图6 机体向上抬头时的俯仰角(左视图)

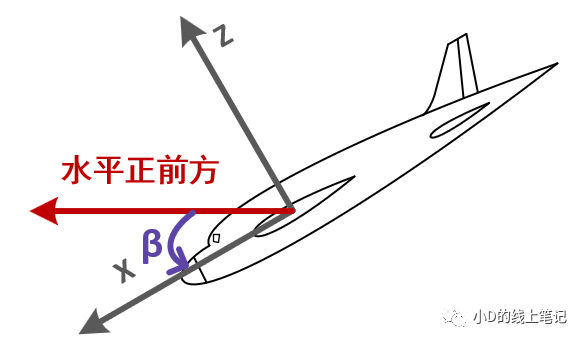
图7 机体向下低头时的俯仰角(左视图)

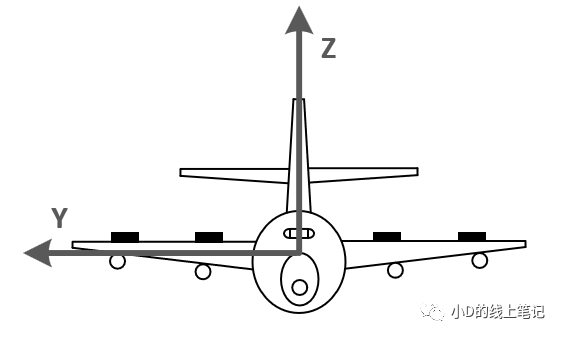
图8 飞机水平飞行时的机体前视图

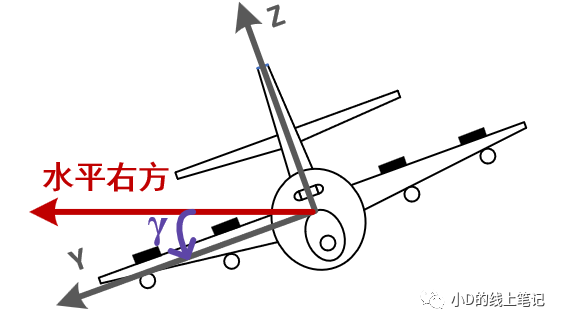
图9 飞机向右滚转时的横滚角(前视图)

注：向左滚转和向右滚转是以飞行员正视前方时的视角判断的

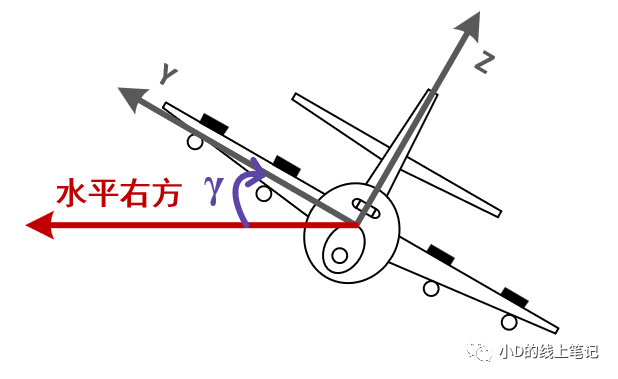
图9 飞机向左滚转时的横滚角(前视图)

上面的图是小D用visio画的，应该可以很好地说明航向角、俯仰角和横滚角。

ENU左手坐标系转换到机体左手坐标系

ENU左手坐标系(导航坐标系)转到机体左手坐标系(载体坐标系)是一个有点抽象的过程，小D第一次看这个转换过程的时候，觉得头都大了，想了好久才想明白是怎么旋转的。为了讲清楚转换原理，小D根据《机载卫星通信天线角度的计算推导》里的图，重新画了一个三维图，希望可以让大家更好地理解这个过程。

下图中，α是飞机的航向角，β是俯仰角，γ是横滚角，大家可以结合小D参考的这篇文献中的解释来看这几个角，小D把截图放在文末了。

紫色的XnYnZn坐标系代表NEU坐标系，灰色的XbYbZb坐标系代表机体坐标系，虚线坐标系是中间过程坐标系。为了不让示意图看起来很复杂，文献以及小D都把ENU坐标系XnYnZn的原点放到了机尾位置，它本来应该是和机体坐标系XbYbZb共用一个原点的。

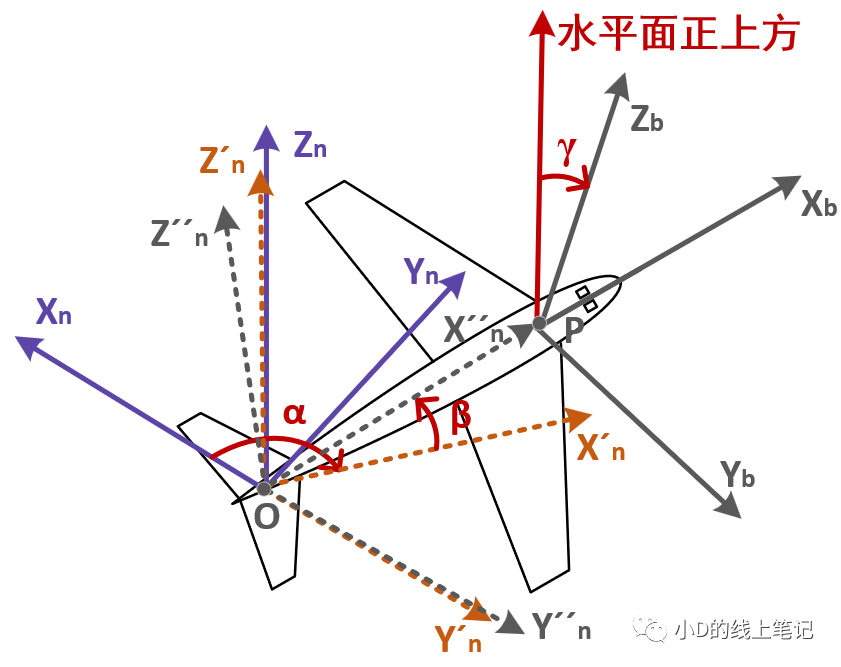
图10 ENU坐标系转换到机体坐标系的过程示意图

现在我们来看看ENU坐标系XnYnZn转换到机体坐标系XbYbZb的整个旋转过程，一共有三个旋转变换：

①XnYnZn坐标系先绕Zn轴顺时针旋转α角，形成X´nY´nZ´n坐标系；

②X´nY´nZ´n坐标系绕Y´n轴逆时针旋转β角，形成X´´nY´´nZ´´n坐标系；

③X´´nY´´nZ´´n坐标系绕X´´n轴逆时针旋转γ角，与机体坐标系XbYbZb重合。

图中没有画出第③个过程，大家可以自己想像一下，或者用模型比划一下，模型小D是用便签纸和胶棒粘的一个三维的空间XYZ坐标系，用来理解空间中的变换过程，大家也可以像小D一样做一个模型。

图11 自制模型

由于上面的过程是左手坐标系的旋转过程，所以顺时针旋转时，计算带入的角度是正的，逆时针旋转计算带入的角度是负的，根据小D上次发的公众号文章中的左手坐标系的旋转矩阵，我们可以计算ENU坐标系XnYnZn转换到机体坐标系XbYbZb的旋转矩阵：

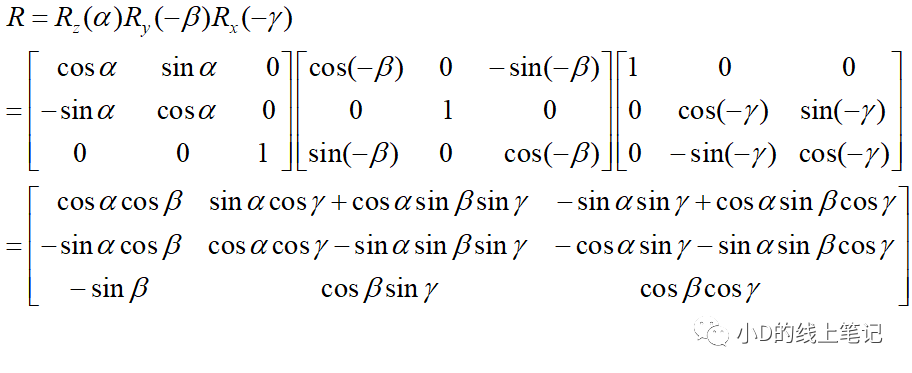
这就是最终的旋转矩阵了。

机体左手坐标系转换到ENU左手坐标系

机体坐标系转到ENU坐标系的过程是一个逆过程：

①XbYbZb坐标系先绕Xb轴顺时针旋转γ角，形成X´bY´bZ´b坐标系；

②X´bY´bZ´b坐标系绕Y´b轴顺时针旋转β角，形成X´´bY´´bZ´´b坐标系；

③X´´bY´´bZ´´b坐标系绕Z´´b轴逆时针旋转α角，与ENU坐标系XnYnZn重合。

所以，机体左手坐标系转换到ENU左手坐标系旋转矩阵为：

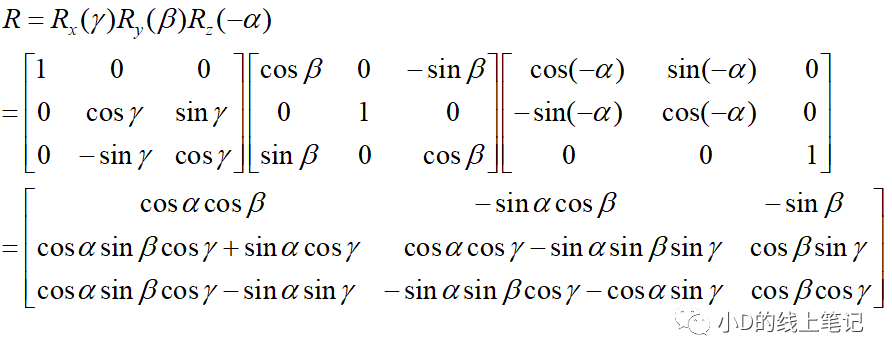
文献中的公式推导

《机载卫星通信天线角度的计算推导》中的转换过程示意图如下图所示，其中U轴是水平面正上方，小D绘制的跟文献中的图有一些不同的地方，就是Zb轴小D觉得应该画在U轴的右边。

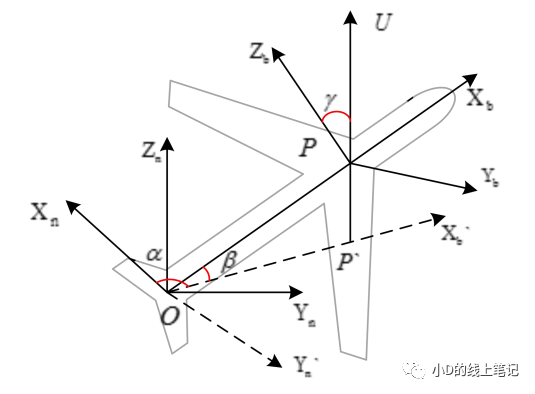
图12 文献中的旋转过程示意图

除此之外，小D觉得文献中给出的绕X，Y，Z轴逆时针旋转的旋转矩阵是有点问题的，正确的旋转矩阵小D在上篇公众号文章中给出了，大家可以对比一下，如果你觉得小D的观点有问题，也可以告诉小D。

文献中关于ENU坐标系（导航坐标系）与机体坐标系（载体坐标系）的推导过程是这样的：

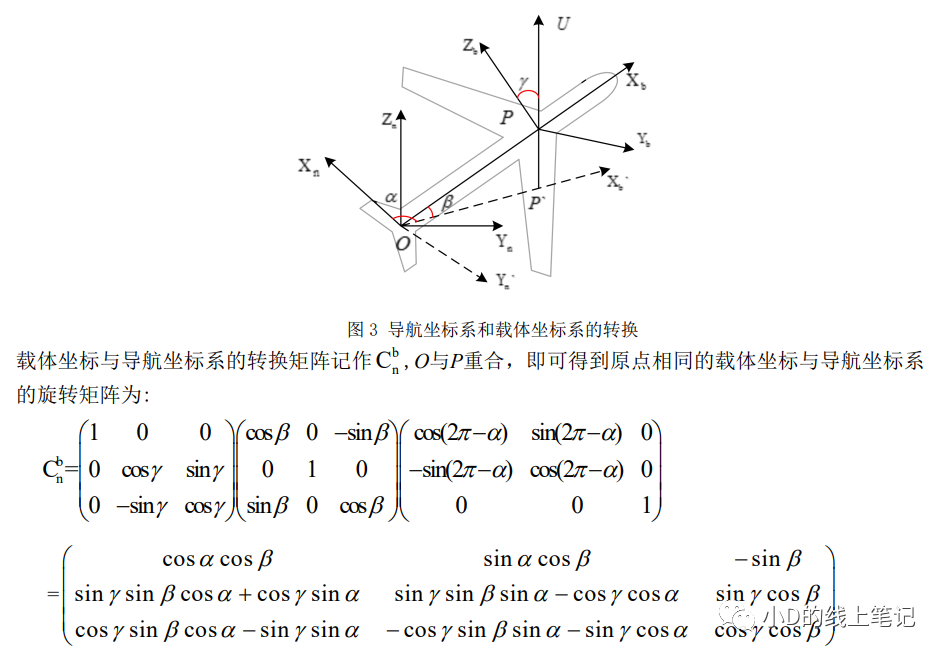
需要注意的是，上面的“逆时针旋转2π-α”与“顺时针旋转α”是等效的。该篇文献的作者讲解的旋转过程是导航坐标系转到载体坐标系的过程，但是计算的旋转矩阵是载体坐标系转到导航坐标系的公式。

还有一点就是，作者可能是笔误，三个矩阵相乘的结果也有一点问题，小D用matlab计算了一下作者给出的三个矩阵相乘的公式，计算过程如下：

图13 旋转矩阵相乘的验证代码

图14 代码计算结果 

代码计算结果如上图所示，和作者计算的不一样，字体有点小，大家可以自己在matlab里验证旋转矩阵计算结果。

审核编辑：刘清