关于网络综合和滤波理论的起源及演进历程

本文是达林顿于1984年所撰写的网络综合与滤波理论发展概述，聚焦RLC电路的演进。电路今日之繁荣，理论发展功不可没。诚邀您搭乘时光之舟，探寻电路历史的趣闻轶事，共鉴科技辉煌。

如下是维基百科对作者达林顿的传记译文(https://en.wikipedia.org/wiki/Sidney_Darlington)：

西德尼·达林顿(Sidney Darlington，1906年7月18日-1997年10月31日)是一位美国电气工程师，于1953年发明了一种晶体管电路结构，即达林顿对管。他推动了网络理论的发展，开发了插入损耗综合方法，并发明了线性调频雷达(chirp radar)、轰炸瞄准器以及枪支和火箭制导系统。

1928年，达林顿以优异成绩获得哈佛大学物理学理学学士学位，并被选为Phi Beta Kappa成员。1929年，他又获得了麻省理工学院的电气工程理学学士学位，并于1940年获得哥伦比亚大学物理学博士学位。

1945年，他由于在二战期间的贡献而被授予美国最高平民荣誉——总统自由勋章。他是美国国家工程院的院士，由于他在电气网络理论、雷达和制导系统方面的贡献。1975年，他获得了IEEE的爱迪生奖章，“以表彰他对网络理论的基本贡献以及在雷达系统和电子电路方面的重要发明”，并于1981年获得IEEE荣誉奖章，“以表彰他对滤波和信号处理的基本贡献，从而促成了线性调频雷达的发明”。

他在美国新罕布什尔州埃克塞特的家中去世，享年91岁。

A History of Network Synthesis and Filter Theory for Circuits Composed of Resistors, Inductors, and Capacitors

电路网络的综合与滤波理论发展史

摘要

本文是关于网络综合和滤波理论的起源及演进历程的非正式历史记述，主要是围绕电路的发展进行阐述。它包含了一些事件、经验和轶事，这些可能并不都有详尽的文档记录，但读起来会很有趣。本期杂志中的其他论文是电路理论其他方面的历史，大部分源自于理论。

引言

这是一篇关于网络综合和滤波器的受邀论文。本期杂志中其他作者的其他历史论文涵盖有源电路、数字电路、非线性电路等。因此，为了避免重复，本文主要关注线性、时不变、电路。然而，将大量讨论理论对其他学科的影响，反之亦然。

我们所知的通用网络综合首先是为电路开发的。真空管电路是相对简单的电路(真空管放大器中的级间电路，振荡器和“再生”无线电接收机等中的简单反馈)。没有运算放大器、晶体管、回转器(gyrators)、阻抗转换器等。因此，电路的网络综合理论是一般综合理论的祖先。

贝莱维奇(Belevitch)在1962年5月IRE会议录50周年特刊上发表了非常好的电路理论发展史。他列出了许多关键贡献和贡献者，注明了出版年份但没有特定的期刊引用。他还指出，为了简洁和可读性，还有许多其他值得一提的贡献者被排除在外。

我不可能改进贝莱维奇到1962年为止的客观、学术性的电路理论历史。自1962年以来，理论取得了重要进展，但除了计算机应用(属于本期CAD论文)外，它们相对较少。电路理论的大多数重要进展都涉及其他类型的电路，如有源、开关或数字电路。

而且，当我试镜像贝莱维奇那样写一篇客观的学术史时，唤起了我的大量个人记忆，这些记忆记录在我半个多世纪以来的技术数据库中。我从小就想成为一名工程师，而且选择了电气工程(可能是为了与我的父亲不同，他是一名机械工程师)。我在哈佛大学乔治·华盛顿·皮尔斯(George Washington Pierce)讲授的调谐耦合电路瞬态课程中，从电力工程转向通信工程(1927年或1928年)，并在麻省理工学院欧尼·纪廉敏(Ernie Guillemin)讲授的传输线课程中，接触到了坎贝尔-佐贝尔滤波器(Campbell-Zobel filters)(1929年，他深入研究通用网络综合的前一年左右)。当我于1929年加入贝尔实验室时，我的第一位老板是埃德·诺顿(Ed Norton, Norton's theorem诺顿定理等等的提出者)。我的第二位老板(从20世纪30年代中期开始)是亨德里克·伯德(Hendrik Bode)。因此，我在通信工程领域早期的成长时期，与网络综合的早期形成时期基本吻合。

所以，本文是一篇学术性较低、主观性较强的历史文章。它包括了一些事件、经历和轶事，这些并不都有详尽的文档记录，但读起来会很有趣。它还包括了关于电路理论对研究它的人以及其他种类工程发展的影响的个人思考。

可以写一整本书来讲述电路、网络综合和滤波理论的历史，包括技术解释、期刊和专利引用以及与其他学科的相互作用。它的准备工作需要比我所能设想的更多的期刊和图书馆研究，而且很难轻易证明其合理性。

一些读者可能不同意对某些人物和事件的引用选择。他们是非常个人化的选择，来自众多的应得引用，只能作为样本。一些从记忆中提取的细节可能在小的方面存在错误，特别是关于很久以前的事件。滤波器理论和网络综合诞生时的高远时代，几乎没有幸存的见证者。坎贝尔(Campbell)、佐贝尔(Zobel)、卡尔(Cauer)、纪廉敏(Guillemin)和其他许多人很多年前就去世了。伯德(Bode)大约在两年前去世，诺顿(Norton)大约在一年前去世。在幸存者中，一个值得注意的例子是福斯特(Foster)。在最近的一次电话交谈中，他透露他正在写一篇关于拓扑学的长篇论文(大约在他著名的“电抗定理”发表60年后)。对于本文中未提及的更多人物、事件和日期的更简短的引用，请参阅。

“网络(network)”一词在这里主要用于“网络综合(network synthesis)”，这在历史上是最为人所熟悉的。在其他地方，同义词“电路”更受青睐。贝莱维奇使用“网络”专门指理想化的电路模型[, p. 849 (脚注)]。但是现在我们也有很多的计算机“网络”、电视台、通信频道等。

本文的其余部分分为以下几个部分：

网络综合之前

原始网络综合

通用网络综合-实现技术

通用网络综合-逼近技术

具有规定插入损耗的电路综合

损耗-相位关系和反馈放大器

电路理论的进一步发展

现在与过去

今后

网络综合之前

“电路分析”用于确定给定电路的特性。“网络综合”则与之相反，它用于确定具有给定(期望)特性的电路。电路分析的发展是网络综合发展的先决条件。首先，必须阐述单个元件的性能(用现代术语来说就是“建模, modeled”)。其结果是欧姆定律用于电阻，电流导数用于电感，电压导数用于电容等。然后，必须阐述互连元件的操作。对于线性时不变电路，基尔霍夫定律导出了具有常系数的电压和/或电流的线性微分方程。

这种微分方程的数学理论当然为人熟知，也应用于经典动力学。对应用于电路的微分方程的理解包括稳态与瞬态响应、叠加定理、戴维南定理和诺顿定理以及互易定理等概念。复数的使用使稳态响应的计算变得更加容易，频率变量在瞬态分析和后来的综合技术发展中都很重要。

海底电缆的发展对电路理论的发展产生了重要影响。最初，人们对海底电缆等传输线的理解很浅。误解导致了严重的实际困难。奥利弗·亥维赛德(Oliver Heaviside)是早期对传输线以及电路理论其他方面理解的重要贡献者。Nahin最近出版了一本关于亥维赛德的传记。最初，亥维赛德的工作并没有得到普遍认可，直到20世纪20年代末他几乎被遗忘了。在他1927年或1928年关于调谐耦合电路瞬态的课程中，G.W.皮尔斯没有包括亥维赛德展开定理。1929年，麻省理工学院的人们正在阅读一本关于亥维赛德运算微积分的新书(据我回忆，这是范尼瓦尔·布什(Vanivar Bush)著的一本书的早期版本)。但是乔治·坎贝尔(George Campbell)一直对亥维赛德感兴趣，他是将亥维赛德的数学应用到实践中非常重要的、非常早期(出生于1870年)的贡献者。

对传输线的理解引入了传播常数(衰减和相位)、匹配阻抗以及非匹配阻抗处的反射等概念。集总加载(最初由亥维赛德提出)是镜像参数滤波器的先驱。接地与平衡线路以及“phantom”电路引入了三端与平衡双端口以及纵向与横向电流的概念。

原始的网络综合

韦伯斯特词典将“proto”定义为“时间上的第一”或“原始的”。在这里，我们指的是在通用网络综合开发之前使用的电路设计技术(以及此后的许多目的，甚至直到现在)。成功的设计技术是为许多特殊目的而开发的。下面提到的例子大多来自1910年代和1920年代。(但是，加载线早在1900年就被证明了。)

滤波器理论首先由加载线(loaded lines)演化而来。一条线结合了分布电感和电容的效应(电感加载增加了有效电感的值，这通常远低于电容的值。)分布加载增加了分布电感本身的值(例如，通过磁性材料包裹在导体周围)。集总加载通过在均匀间隔的点处在线中插入集总电感来近似这种效果。亥维赛德提出了分布加载和集总加载。他的建议没有被广泛接受，因为人们认为增加的电感会延缓信号的传输。当然，实际上它确实会延缓传输，但这只是延迟的增加，同时延迟失真减少。

后来，坎贝尔(AT&T公司)和普平(Pupin)都申请了关于集总加载的专利。由于亥维赛德已经发表了这一概念和原理，因此尚不清楚他们到底声称什么可能是实践上的减少。普平赢得了专利诉讼，并将独家权利卖给了AT&T公司。“加感线圈”大大增加了在真空管中继器出现之前进行电话通话的实际距离(但只有在改进电感的发展之后，这需要大量的实验)。

如果加感线圈足够接近，连续加载可以被集总加载替代，这并不奇怪。当电感的大小和间距减小到零时，就是连续加载的极限。工程问题是：它们可以放置多远？为了回答这些问题，分析了加载线的传输特性。事实证明，如果其频率不超过与加感线圈的间距和大小相关的“截止频率”，则沿非耗散加载线传播的正弦信号将遭受零衰减。在较高频率下，信号会被衰减。因此，加载线是一个低通滤波器。将分布电感减小到零只留下集总电感是简单的一步。然后可以合理地增加集总电容加载，并将分布电容减小到零。

其结果是集总低通滤波器(其所有传输零点都在无限频率处)。它具有“梯形”电路结构(configuration)：线路中的交替“串联支路”和跨线路的“并联支路”。坎贝尔还公开了全通格型网络(1920-1922)。人造传输线(Artificial lines)和衰减器(attenuators)很早就被开发出来了，并且至少有一些使用了梯形电路结构。

坎贝尔和瓦格纳(Wagner)在第一次世界大战期间独立发明了这种滤波器。至少在坎贝尔的情况下，历史更为复杂，大致如下：1911年，AT&T就坎贝尔的滤波理论提交了专利申请，但没有付诸实践。1913年，建造和测试滤波器的提议被放弃，因为这似乎“在物理上没有多大影响”。1915年，弗兰克·朱厄特(Frank Jewett, AT&T的助理首席工程师，后来是贝尔实验室的第一任总裁)写了一封信，敦促确保“最大的专利保护”的重要性。这封信包括以下两段话：“这件事高度技术化，涉及与电路网络相关的相当多的数学物理学，这是很少有工程师能掌握的学科”，并在结尾处写道：“你可能不同意我的这个建议，但我强烈认为，如果我们让这件事不了了之，我们迟早会在以后的某个早晨体会到后悔的滋味。”

滤波理论包括滤波段(filter sections)、镜像阻抗(image impedances)、镜像衰减(image attenuation)和相位(phase)的概念。用这些术语来说，从加载线导出的滤波器可以描述为相同基本段的串联连接。由于镜像阻抗在段之间是匹配的，因此整个滤波器的镜像衰减和相位是各个段之和。奥托·佐贝尔(Otto Zobel)发明了简单的滤波器段，具有与原始迭代滤波器相同的镜像阻抗以及通带和阻带，但具有不同的镜像衰减和相位特性。特别是，他的“m推演”部分给出了更陡峭的截止特性，并在任意有限频率处产生了衰减峰值。通过将他的m推演段在中间分开，他获得了在滤波器末端的镜像阻抗，该阻抗在通带频率上的变化较小，从而减少了终端反射损耗。

在滤波理论发展的同时，双端口的一般概念在德国和法国被引入。引入了相应的阻抗、导纳和链矩阵(2×2的频率函数矩阵，chain matrices)，并用于计算串联、并联和级联连接的两端口的相应矩阵。

现在有了开发滤波器设计技术的科学基础。除了设计低通滤波器外，还设计了高通、带通和带阻滤波器的附加滤波器段。有一段时间，电路理论家可能会通过发明另一种滤波器段来提高自己的知名度。多年来，大量的技术(Art)被添加到科学中，其结果是出现了大量满足许多实际要求的实用滤波器。

在20世纪30年代，伯德(1934)和皮洛蒂(Piloty, 1937-1938)以及卡尔引入了一种更系统的镜像参数滤波器理论方法。在这里，人们研究整个滤波器的开路和短路阻抗与镜像阻抗以及衰减和相位函数之间的关系。镜像阻抗由相应开路和短路阻抗乘积的平方根表示：。镜像阻抗在理论通带上是实数，在阻带上是虚数。这要求通带内的或的零点和极点被或的极点或零点抵消，当它们出现在阻带内时，和的零点和极点是相同的。匹配奇点的任意位置决定了镜像阻抗以及镜像衰减和相位随频率变化的方式。

调谐电路(Tuned circuits)也是一种简单的(带通)滤波器。它们对无线电接收机的发展至关重要。调谐耦合电路可以提供相当平坦的通带，当截止频率不需要非常陡峭且对通带平坦度的要求不是很严格时，这种电路的级联非常有用。在无线电接收器中，通过联动可变电容将通带定位在频率刻度上，后来通过调整阿姆斯特朗(Armstrong)的超外差接收器(superhetrodyne receivers)中的外差振荡器(the hetrodyne oscillators)来定位通带。

除了滤波器之外，还开发了其他电路。均衡器(Equalizers)被用于各种目的。莎莉·佩罗(Sally Pero, 后来的Sally Pero Mead)设计了一款非常早期的专用均衡器。据我所知，它是一个简单的单端口跨接在接收器上，用于海底电报电缆，旨在允许以更快的速率传输电报信号。我不知道它是更多地校正相位失真还是幅度失真。电报信号是脉冲，以相当低的速率传输。在陆地上，脉冲由机电继电器再生。在海洋下，中继器无法使用，失真限制了每秒可传输的脉冲数。

奥托·佐贝尔的“恒定电阻均衡器段, constant resistance equalizer sections”取代了其他更基本的均衡器。由于它们的镜像阻抗与频率无关，因此恒定电阻部分可以级联连接并电阻端接，没有反射。定阻全通格型网络允许相位均衡和接近恒定延迟(但它们是平衡的四端口，而不是接地的三端口电路)。

人工延迟线(artificial delay lines)的早期应用之一是乔治·华盛顿·皮尔斯所开发的水听器系统(hydrophone system)。(他在哈佛大学讲授水听器工程课程，据称这是世界上唯一一门此类课程。)皮尔斯的系统是对第一次世界大战中使用的纯声学水听器的电气改进。用现代术语来说，它是一种使用二元阵列接收器的被动声纳。方向测量需要一个(可允许的分段)可变延迟。皮尔斯使用了简单滤波器状三端节的迭代。每个节包括一对耦合串联电感和一个从它们的公共点到地的电容。这是一个低通滤波器部分，其，它将传输零点置于实数(虚数)。适当的耦合系数提供了比未耦合电感更线性的相位()。我记得，皮尔斯的专利被贝尔系统购买或许可。

电话工程师越来越需要多端口变压器或变压器的组合。例如抗侧音混合线圈(antisidetone hybrid coils)，幻影分离(separation of phantom)和普通平衡线(纵向与横向电流)，以及双向和一对单向传输系统之间的连接。1920年，坎贝尔和福斯特发表了一篇关于电阻终端非耗散四端口最佳能量关系的论文。贝莱维奇描述说，这可能是关于网络综合真正意义上的第一篇出版物，包括网络的双共轭性(biconjugacy)、所有实现的穷举以及明确由理想变压器组成的电路。当然，这一切都使用了等效电路的概念。

福斯特曾讲述了关于理想变压器四端口组合的穷举的以下故事：可以有不同数量的变压器，具有不同数量的绕组，以不同的方式相互连接到各个四端口。起初，坎贝尔和福斯特发现了一些看起来很有用的电路，并要求他们的专利部门申请专利。专利律师回答说，如果有其他等效电路(可以用来规避专利)，那么申请其中一些电路的专利是没有用的。他们应该全部申请专利或者不申请。因此，坎贝尔和福斯特着手穷举所有等效电路。他们得出了如此大的数字，以至于认为申请所有专利是不可行的(有83,539个不同的电路)。因此，他们决定公布穷举结果，从而排除其他人可能想要使用的特定实施例申请专利的可能性。

理想变压器不仅在理论上很有用。它们实际上在许多带通滤波器设计中都得到了实现，这是通过电路等效性来实现的，如图1所示。图1中的左路电路是一个三端两端口“L”电路，包括一个阻抗为的串联支路和一个阻抗为的并联支路。比率必须恒定(与频率无关)，但和可以分别与频率的函数成正比。该电路与一个阻抗为的并联支路，后跟一个阻抗为的串联支路，后跟一个理想变压器的电路完全等效。假设和是所需滤波器的一部分，并且希望添加理想变压器。可以通过将组合替换为分支和来实现相同的效果。如果和都除以，则可以将变压器移动到相应“L”的另一端。对于从左到右的传输，在图中所示的电路中，它始终是一个降压变压器。对于升压变压器，请将两个电路分别转动。当大于所需的变压器比率时，串联阻抗和/或并联导纳可以分为两部分，其中只有一部分用于图1的电路中。

通过“转动L”来实现理想变压器是带通滤波器设计的常用手段。我第一次是从诺顿那里了解到的，但不知道他是不是第一个发现它的人。当然，许多其他电路等效性也用于滤波器设计，例如等效的“T”和“”以及一些格型的“桥T”等效。

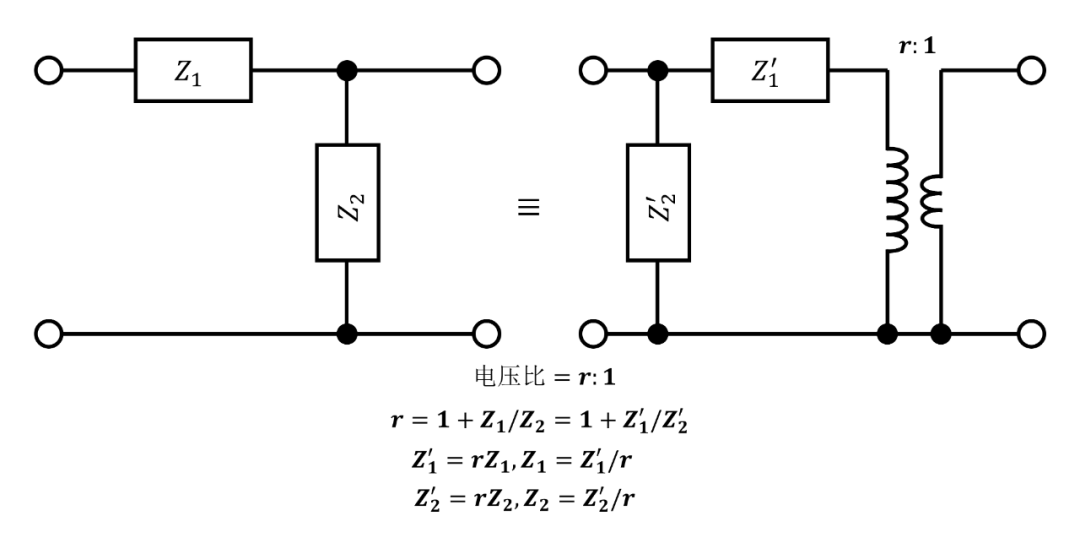
图1. 理想变压器的实现。

通用网络综合-实现技术

通用网络综合理论包括两部分：实现技术(realization techniques)和逼近技术(approximation techniques)。第一部分在20世纪20年代和30年代初就已经形成，相比前一节中描述的更为专业的技术，它描述了更通用的电路设计方法。

不同类型的电路需要不同的实现技术，但一般来说，它们只在共同的一组主要部分的细节上有所不同。第一种“完整”的实现技术涉及LC单端口。所有可能的LC单端口都可以被视为电路的一个抽象类。电路类中的电路产生的各种阻抗可以被视为函数(频率)的一个抽象类。福斯特电抗定理(1924年)建立了用数学术语定义函数类的必要和充分条件。

对应于函数类中的每个函数(除了最简单的)，有许多“等效”的单端口网络，它们具有相同的阻抗但电路结构不同。可以选择一种或另一种电路结构来定义电路类的“规范”子类，以便它可以用来实现函数类中的任何阻抗函数。四个众所周知的规范单端口网络是：并联连接的串联谐振，串联连接的并联谐振(福斯特型)，带有串联和并联的“梯形”，或反过来(卡尔型)。对于函数类中的任何函数，可以通过直接计算找到四个规范电路中任何一个的元件值。贝莱维奇 指出，福斯特的电抗定理(1924年)是“从分析动力学到现代网络综合的过渡”，但“第一篇明确处理实现单端口网络的论文，其阻抗是频率的函数，是卡尔 1926年的贡献”。但福斯特回忆说，他与卡尔在1924年至1926年间就有关于卡尔论文的通信，这是他1926年的论文。

许多其他类型的电路的实现技术遵循类似的模式。表I以一般术语列出了主要部分。(另见福斯特关于电路理论理论方面的论文)。

Brune在1931年发表了他的单端口网络实现。对于表中的第3项，他引入了正实函数(PR)的概念，这与他的规范电路结构一样重要，经常使用许多互感。后来，发现了避免互感的电路结构，但要以额外的元件为代价(Bott和Duffin，1949年)。

福斯特的单端口网络定理很快被扩展到双端口网络。第一篇论文假设对称双端口网络，但在1931年，卡尔解决了所有双端口网络甚至n端口网络的一般问题。卡尔的规范电路包括许多互感和其他不理想的特性。后来发现了更有用的等效电路。

表I

电路类型(元件类型、端口数量，有时还包括电路结构限制)。

相应的频率或时间函数类(导纳，或导纳矩阵，或脉冲响应等)。

必要和充分条件，以数学术语定义函数类。

涵盖函数类的电路类的规范子类。

一种直接计算与函数类中任何给定函数对应的规范电路元件大小的过程。

从那时起，随着实际需求和可用元件的激增，已经衍生出许多其他实现技术。参考文献是一篇关于实现技术的综述，发表于1955年。它包括一个包含21个完整实现技术的表格，如上所述。它们在电路类上有所不同，由元件类型和电路电路结构类型(单端口网络、双端口网络、端口网络、三端或平衡电路、是否允许互感)定义。它们在由函数类表示的特性上也有所不同(驱动点导纳、双端口网络或口网络的完整导纳矩阵、传输导纳、仅插入损耗、脉冲响应时间函数等)。

该表绝不是1955年已知的实现技术的详尽清单，当然自那时以来已经设计了更多的实现技术。

还有其他或多或少不完整的实现技术(如上定义)。一个例子是没有互感的三端梯形滤波器。函数类包括大多数实用的滤波器函数。已知没有互感的一些充分条件，以及更可能需要它们的一些条件。但是，定义函数类的完整必要和充分条件要么未知，要么至少不是以易于应用的形式出现。

通用网络
综合-逼近技术

在大多数电路设计问题中，理想特性只能逼近得到。就表I而言，函数类中没有与理想外部特性完全匹配的函数。然后，问题是根据一个或另一个标准在函数类中找到最能逼近理想的函数。最著名的逼近技术是应用于滤波器设计的那些技术，假设理想滤波器具有完全平坦的通带和无限衰减的阻带。

1930年，巴特沃斯(Butterworth)在多级放大器的设计中使用了最大平坦度逼近。最大平坦度逼近使得在特别重要的频率处(对于调谐耦合电路为中频，对于低通滤波器为零频)的导数值为零。大约在同一时间，或者可能稍早一些，诺顿将最大平坦度的概念应用于机电和机械声学设备的设计。

诺顿的工作与电动记录器有关，用于切割蜡质母版留声机唱片和改进的机械声学唱片播放器。(贝尔实验室为Victor Talking Machine Co.开发了这些产品。)诺顿根据等效电路设计了放大器到切割唱针和唱针到指数号角机构的电路。(质量由电感建模，柔顺性由电容建模，阻尼由电阻器建模。)等效电路类似物具有低通滤波器的电路结构，仅在一端端接。诺顿设计了滤波器以获得最大平坦度响应。我相信“Orthophonic Victrolas”在巴特沃斯的论文发表之前就上市了，但从诺顿的评论(我几乎不记得了)来看，他的最大平坦度设计可能是针对后来的模型。

至少从某种程度上说，诺顿的工作象征着电路理论的成熟。早期的电路分析大量借鉴了之前振动机械系统的分析动力学。诺顿可能是第一个扭转类比的人，用更先进的电路理论来设计机械系统。

1931年，卡尔将“切比雪夫意义上的逼近”引入电路理论，对此，“极小极大逼近”是一个更简单的现代术语(使最大误差最小化)。他推导了常数镜像阻抗的可实现切比雪夫逼近，适用于理论通带的任意部分。他还推导了无限衰减的切比雪夫逼近(使最小衰减最大化)，适用于理论阻带的任意部分(除了变量变化外，是相同的数学问题)。在每种情况下，它们都假设了由滤波器复杂度确定(或决定)的任意数量的任意参数。

在贝尔实验室，我们中的一些人首先在卡尔提议出售他的一些专利的会议上了解到卡尔的一些规范电路和他的切比雪夫逼近。这是我职业生涯中的一件大事。

卡尔的专利在没有证明的情况下陈述了他的切比雪夫公式。谢尔盖·谢尔库诺夫(Sergei Schelkunoff)很快为我们提供了证明。同时，他构思了一个新的通用定理(不需要用于那个特定问题)，该定理适用于所有具有“等波纹”解的切比雪夫问题。我仍然在寻找更多的新应用。

规定插入损耗的电路综合

镜像参数滤波器受到方法固有的开路和短路阻抗的大部分零点和极点的必需抵消或重合的限制。实际插入损耗不是直接选择的，而是通过校正所选线路类型的反射和相互作用(多次反射)衰减来选择的。

另一种方法是直接指定插入损耗函数，并据此确定电路。一般的插入损耗理论之前由诺顿的恒定电阻滤波器对(于1937年发表，但于1930年代初发明)。诺顿的滤波器对在一端并联(或串联)，它们一起在公共端提供恒定的电阻。诺顿表明，每个滤波器都像一个在一端仅由电阻端接(在另一端由开路或短路端接)的单个滤波器。他选择了适合他的恒定电阻对滤波器的插入损耗函数，从中找到了滤波器在其终端端的开路或短路阻抗，并推导了从开路或短路阻抗计算梯形电路结构中的元件的步骤方法。

更一般的插入损耗理论由科奇(Cocci, 1938-1940)、达林顿(Darlington, 1939)、卡尔(Cauer, 1939-1941)和皮洛蒂(Piloty, 1931-1941)独立开发。一般理论由几个主要部分组成。从以下实现技术开始，在表I的意义上：电路类是插入在输入和输出电阻之间的所有双端口的类。感兴趣的频率函数是“功率比”，其中是输出电阻两端的电压，是可能的最大(对应于两个电阻之间的阻抗匹配变压器)。函数类是对应于电路类中所有电路的所有此类函数的类。对函数的必要和充分条件要求是频率平方的非负有理函数，任何地方都不超过1。

可以从任何这样的函数中找到相应的双端口的开路和短路阻抗。找到这种关系是一般理论发展的一部分。可以证明，阻抗满足卡尔关于双端口的条件。然后卡尔的规范双端口成为一般插入损耗理论的一个规范电路。

卡尔的规范双端口为插入损耗函数提供了必要和充分条件，但对大多数实际应用来说并不令人满意。插入损耗理论的第二个主要部分确定了另一种规范的双端口，该端口由级联连接的简单“节”组成。对于一般的双端口，可能需要四种类型的部分。串联单端口、并联单端口、由并联电容隔开的一对耦合串联电感的“”，以及具有两倍元件数量但仅在复杂频率下传输零点所需的部分。(为了完全通用，还必须在双端口的一端包括一个理想变压器，如果终端电阻的比率取决于设计者的选择，则插入损耗理论中不需要)。 大多数实用滤波器可以排列成交替串联和并联单端口的梯形电路结构，并且没有互感。

作为实现技术的推论，发现了新的规范一端口。它只有一个电阻，但通常需要一些冗余的无功元件和一些耦合电感。它在与频率相关的阻抗匹配方面有一些用途。

插入损耗理论的下一个主要部分涉及插入损耗滤波器的逼近技术。为了有效地使用元件，通常选择零损耗和无限损耗的频率为实数。然后，功率比可以写成，其中是频率的奇或偶函数。零损耗的频率是的零点，传输零点是的极点。增加(正)比例因子会增加阻带损耗，但代价是通带上的损耗变化增加。的零点和极点以及比例因子可以任意选择。然后可以简单地计算任何频率下的插入损耗。

顺便提一下，当为奇时，相应的滤波器是(外部)对称的；当为偶时，它们是反对称的。

切比雪夫或最大平坦度对应于切比雪夫或最大平坦度插入损耗。对于切比雪夫或最大平坦度通带，是在通带频率上接近零的切比雪夫或最大平坦度逼近值；对于切比雪夫或最大平坦度阻带，是在阻带频率上接近零的切比雪夫或最大平坦度逼近值。切比雪夫通带和阻带都可以在同一滤波器中实现。找到了低通和高通滤波器的设计技术，并从中推导出了其他设计技术。它们使用雅可比椭圆函数，不同于但类似于卡尔用于镜像参数滤波器函数的那些函数。

发现了其他通带和阻带特性组合的设计技术，包括最大平坦度通带和阻带、切比雪夫通带和最大平坦度阻带、最大平坦度通带和切比雪夫阻带，以及切比雪夫通带和任意阻带传输零点。

还开发了从功率比函数计算元件大小的方法。首先找到的极点，并从中得到复频率函数和端接电阻处的复反射系数。由此，可以很容易地得到双端口的开路和短路阻抗函数。最后，使用基本的诺顿步骤方法从一个或多个阻抗中计算滤波器元件。(后来，各种电路理论家对其进行了改进和完善，尤其是降低了对计算舍入误差的敏感性，这种误差可能很高。)

我的插入损耗理论还包括第四部分。伯德发现了一种对频率变量的简单变换，由此可以计算用具有相同品质因数Q的有耗电感和电容替换所有无耗电感和电容的效果。将伯德的变换反过来，可以得到无耗电感和电容的“预失真”电压比，从而在用电感和电容替换为有相同(指定)品质因数Q的有耗元件时获得所需的电压比(除了平坦损耗外)。

与镜像参数滤波器一样，科学的骨架必须通过大量的技术来充实以进行实际设计。插入损耗滤波器设计方法直到几年后才被普遍接受。它必须与经验丰富的、高技能的滤波器设计师使用的既定镜像参数方法进行竞争。通过插入损耗方法获得的滤波器通常更好，但并不比镜像参数对应物好很多。插入损耗设计所需的大量计算是一个严重的缺点。

计算机和非滤波器的出现改变了这种情况。例如，级联双二阶有源滤波器的设计就不需要计算插入损耗滤波器的梯形元件，只需要计算电阻端接镜像参数滤波器的极点。

上述引用的日期是出版日期。考虑到插入损耗理论的广泛性，每篇出版物之前可能都进行了相当长一段时间的研究。我的研究始于20世纪30年代初。我的初步灵感来自诺顿的恒定阻抗滤波器；福斯特、卡尔和Brune的实现技术；以及卡尔的镜像参数滤波器的切比雪夫逼近。到1933年，我知道如何计算对称和反对称的切比雪夫滤波器，但(我相信)我还没有证明端接电阻之间双端口的规范性质。1936年，我写了一套通用的笔记供贝尔实验室内部使用(超过400页的打字)。它几乎包括了1939年出版的所有内容(以及更多的细节)，但并不完全包括。该出版物的手稿于1938年5月被《数学与物理学杂志》的编辑收到，但直到1939年9月号才有空位出版。(译注：这篇文章已经被翻译为中文版本，请在公众号内部查找《综合特定插入损耗指标的LC四端口网络》)

同时需要切比雪夫通带和阻带的雅可比椭圆函数，在19世纪的各种文献中都有描述。在纽约市，纽约图书馆，人们可以查阅雅可比于1829年用拉丁文发表的原始论文。值得注意的是，有折页列出了椭圆函数变换，包括直接适用于镜像参数和插入损耗切比雪夫逼近的变换。

损耗-相位关系与反馈放大器

网络综合的一个完全不同的重要部分涉及反馈放大器(以及类似的自动控制系统)。哈罗德·布莱克(Harold Black)发明了具有环路净增益的负反馈放大器。奈奎斯特(Nyquist)提供了他的标准(译注：也就是现在所谓的奈奎斯特稳定性判据)，它表明了一个给定的放大器是否稳定。但那是电路分析。稳定反馈放大器的设计仍然是一个网络综合问题。

问题的关键在于现在著名的损耗-相位关系(译注：这里也可以用增益-相位关系)。它们允许相位根据给定的损耗进行计算，反之亦然，通过某些积分，假设电路稳定。特别是，它们可用于关联打开的反馈环路周围的损耗和相位，这是应用奈奎斯特标准的初步。贝莱维奇引用了各种关于损耗-相位关系数学的早期出版物。其他人可能会被包括在内。

在20世纪30年代中期，必须为第一个同轴电缆电话传输系统中的中继器开发高效的反馈放大器。我们在《数学与物理学杂志》上发表了一篇关于损耗-相位关系的论文，作者是维纳( Wiener )和李( Lee )(我不记得日期了)。我们认识到这些关系可能很重要，但正如所发表的那样，它们有两个困难。数学表明存在多个解，但没有物理解释。这些关系以积分的形式出现，没有深入了解损耗如何影响相位。伯德消除了这两个困难。他确定并定义了“最小相位”，并表明所有其他允许的相位与之相差“全通”相位。他将经典的损耗-相位积分转化为等效的积分，从而提供了所需的洞察力。这需要将积分变量从频率更改为频率，然后进行部分积分。结果是现在著名的每倍频程分贝规则(译注：这也是波特图的来源)。给定频率下的最小相位是损耗相对于所有频率的对数频率的导数的加权平均值。

从每倍频程分贝规则出发，伯德开发了一套广泛的综合理论和技术来设计反馈放大器。它包括理想的环路增益特性、由于前向电路渐近行为而对反馈和/或带宽的限制、定义“电阻效率”的积分等，以及同轴电缆系统所需的可变均衡器。这项工作中的一些使用了当时电路工程师通常不熟悉的经典函数理论。

在二战之前，就已经通过伯德的方法设计了高效的放大器。他于1945年出版的关于反馈的经典著作与他战前为贝尔实验室课程所写的笔记几乎没有什么不同。

电路理论的进一步发展

电路理论的一般发展，特别是网络综合的发展，变得越来越多，具有极其复杂的相互关系。作为衡量电路理论活动的一项指标，贝莱维奇 使用每年发表的电路理论论文的数量：1910年前少于1篇，1920年至1940年间为5至25篇，1954年后 > 100篇。在1973年关于“跳跃式”有源滤波器的一篇论文中，圣特尔迈(Szentirmai)指出：“在过去的二十年里，如何实现规定的频率有理函数的问题......是通过有源结构实现的，这是超过一千篇学术论文的主题。” 

电路理论的新发展利用了其他学科的新发展：新元件、新的通信需求、新的计算机需求等。相反，电路理论和实践的新发展也引发了其他学科的新发展。它们数量众多，无法在这篇论文中详细描述。无论如何，从更一般的角度来看这些相互作用会更有趣。

表II比较了四列中各个学科的增长。它并不包括所有可能的学科。它只是说明了增长的复杂性。在表中，时间向下增加，不一定是线性的。一个项的垂直位置应该代表它何时首次对电路理论变得重要(在不一定线性的时间尺度上)。但这样的时间是极其模糊的。许多项目都是从一个小起点开始，在很长一段时间内变得重要。

用其他系统来模拟电路理论的发展是很诱人的。一个模型是挂毯。从正面看，不同的观看者会看到不同的图案。从背面看，人们只能看到纠结的线团。一个更有活力的模型是代表电路理论的河流，由代表其他技术的支流提供。这些支流将电路理论从涓涓细流提升为具有许多相互作用的宽阔河流。但是计算机能被描述为仅仅是电路理论的支流吗？

其他可能性更加以自我为中心。一个是族谱的。当今的电路理论可以被视为来自许多祖先的后代，其中前几代的电路理论只是男性血统。其他祖先包括元器件技术、计算机等。但是家谱模型对于谁是谁的后代提出了艰难的抉择。(A能同时是B的父母吗？B是A的父母吗？)

表 II

(虚线以上的项是促成现代电路理论诞生的早期发展)

最好的以自我为中心的模型可能是社会学(或人类学)的：许多部落，他们的文化因频繁的通婚而丰富。例如，有崇拜电路理论的部落和崇拜计算机的部落。每个部落的许多成员都与另一个部落无关。(而且每个部落中真正工作的人对另一个部落的增长知之甚少，也不关心。)但是所有的部落都从无数的通婚中获得了巨大的利益。而且肯定已经发生了人口爆炸。

以下例子可能很有趣：每个人都知道计算机对电路理论产生了巨大的影响。早期在另一个方向上的交叉施肥就不那么为人所知了。20世纪30年代末，乔治·斯蒂比茨(George Stibitz)利用电话交换元件发明了一台电子计算机。它有一个以电传打字机为形式的“终端”。输入数字和指令，计算机就会输出答案。1940年，它在位于新泽西州汉诺威的“终端”和位于纽约市贝尔实验室壁橱里的“CPU”上进行了演示。这台机器只执行复数的简单算术运算，但其设计引入了几种新颖的想法和概念，这些想法和概念此后被用于更大的计算机中。

斯蒂比茨专门为复数算术设计计算机并非偶然。在斯蒂比茨工作的贝尔实验室，电路开发部门对更好的复数算术运算方法有着迫切的需求。他们在电路分析中使用大量的常规复数算术运算来检查新电路设计的响应。复数算术运算是由台式计算机上的一系列正实算术运算来执行的。这项工作很繁琐，而且很难避免偶然的错误。(这是由被称为“计算员”的女性完成的；那是性别歧视的日子。)

显然，表II中的许多项目都应该有更详细的个人历史。有些内容在本期的其他论文中有所涉及(有源电路、数字电路等)。下面简要介绍其他一些内容。

二战推动了特殊用途信号处理电路和优化理论的快速发展。撷取一小部分是：用于雷达发射机的脉冲发生器；用于减少雷达接收机噪声的最佳脉冲形状(理论)(“北滤波器North filters”等)；用于雷达显示的距离测量和扫描电路；运算放大器的发明(Och和Swartzel)；用于模拟高射炮火控计算机的运放平滑和预测电路。最后一项启发了诺伯特·维纳(Norbert Wiener)著名的关于高斯信号平滑和外推的二战论文。鲁迪·卡尔曼(Rudy Kalman)的状态空间平滑和预测稍后出现，并找到了许多应用。当然，战时高频电子技能的发展对战后电视的发展起到了巨大的推动作用。迪佐尔德(Dietzold)的一项专利引用了-单运放电路作为实现一般传递函数的一种手段。

卡尔曼还引起了人们对状态空间在经典电路分析和综合中的应用的广泛兴趣。其实，状态空间的概念由来已久。在电路理论的早期历史中，人们谈论“自由度(degrees of freedom)”和“自然模式(natural modes)”。事实上，亥维赛德的展开定理是将状态空间应用于电路脉冲响应的计算。数学家们早就将阶标量微分方程转化为1阶向量微分方程。不同的状态空间应用使用不同的状态空间(在线性电路的情况下线性相关)。现代对状态空间电路理论的兴趣始于一个空间，在这个空间中，空间的维度与电路元件之间存在一一对应的关系。这通常从一个奇异矩阵开始，但巴什科夫(Bashkow)展示了如何将其简化为他的非奇异“矩阵”。

横向滤波器(译注： transversal filters ，抽头延迟线滤波器，有限脉冲响应滤波器)的概念早于表II建议的时间。在早期(或可能是20世纪30年代中期)。维纳和李为逼近频率的任意函数申请了一种电路的专利。(另见参考文献中的傅里叶级数。)它由一个相同的全通段级联组成，信号输入在一端。输出在段之间取出，乘以任意常数因子，然后相加。输出被描述为变换频率变量(由单个部分的频率响应确定)中的截断傅里叶级数。然而，直到宽带时间函数变得重要，如在雷达、电视和高速数据传输中，横向滤波器才受到关注。

对电路理论的拓扑方面的浓厚兴趣大约始于20世纪30年代中期。福斯特是该领域的早期爱好者，他的兴趣一直持续到现在。拓扑通常关注没有变压器或互感的电路，通常是n端口。要了解更多历史，请参阅本期关于拓扑的论文。

散射参数最初是为分布元件(如线路)开发的，但也有效地应用于集总元件电路，包括插入损耗滤波器和阻抗匹配。

电路理论训练对人的影响也可能很大。许多曾经的电路理论家都转向了系统理论。理想情况下，像表I这样的表格也可以成为许多其他工程设计领域的目标。但通常，实际复杂性或理论困难使理想与现实相去甚远。电路理论似乎特别令人满意，也许是因为理论模型非常接近现实，数学问题可以用不太困难的方法解决。它可以是一个重要理想的有价值的例证(特别是当由像欧尼·纪廉敏这样的伟大教师教授时)。

另一方面，我记得那些过于热情的电路理论家，他们似乎认为像表I这样的系统组织对工程来说是新的。这是一个非常古老的例子：考虑一个围绕行星运行的航天器(设备类)。艾萨克·牛顿爵士发现了由于引力引起的天体运动的微分方程(我们的函数类是两体问题的特例，其中一个物体的质量远小于另一个物体)。对于两个物体，他证明了轨道必须是椭圆形的、抛物线的或双曲线的，并找到了尺寸与速度等关系的公式(用数学术语定义我们函数类的必要和充分条件)。只要航天器的重量与行星相比很小，不同重量的航天器就会描述相同的轨道(任何一个都可以是规范子类)。最后，几个世纪后出现了“霍曼转移椭圆”，这是将航天器从一个椭圆轨道转移到另一个椭圆轨道的最有效轨道。

现在与过去

1939年，在麻省理工学院，电气通信是VIC部门，与普通电气工程VI部门相对应。幸运的是，那一年正好讲授了滤波器理论——在一门关于通信传输线路的学期课程结束时。现在，通信、计算机和控制的电子学使电力工程相形见绌。在四年的工程课程中，要彻底教授电子学的所有重要方面已经不可行了。

在20世纪20年代和30年代，跟踪电路理论的出版物并不太难。现在，仅IEEE电路与系统学会的“国际研讨会”就能产生超过一千页的研讨会“会议记录”。

在20世纪20年代，人们很幸运地能找到一种满足设计需求的电路(对于滤波器：电阻终端LC梯形电路)。现在，人们必须在许多完全不同的电路类型之间进行选择(对于滤波器：、机电、运算放大器(在众多电路结构中的任何一种)、数字、开关电容、横向、微波等)。给定应用的最佳设计取决于众多实际考虑之间的平衡。

另一方面，特定类型的滤波器可以结合为其他几种滤波器开发的设计理论。这里有一个例子。从RLC梯形电路结构开始。根据切比雪夫(椭圆函数)对理想滤波器的逼近，找到元件尺寸。用运放等效物替换。用开关电容替换所有。开关电容滤波器对信号进行采样。开关可以这样安排，使得数字滤波器理论的“双线性变换”适用。在原始的设计中，使用双线性传递函数来调整滤波器截止频率值。最后，将整个开关电容滤波器集成在一个芯片上。

有三种不同的逼近技术可用于获得具有(或多或少)平坦通带和高损耗阻带的滤波器：镜像阻抗滤波器、插入损耗滤波器和调谐耦合电路。插入损耗滤波器通常能更有效地利用元件。对于设计，它们需要更复杂的计算，但计算机通常是可用的。但是，对于一些流行的运放电路结构，插入损耗和镜像参数滤波器的计算大致相同。

当然，人们知道调谐耦合电路对已经很长时间了。一种概括是两个以上调谐电路的串联连接，每个调谐电路与下一个调谐电路之间有耦合。耦合可以是感性的或容性的。我被告知，在可靠的权威下，通过“调整”两个以上调谐电路的电容耦合级联中的所有电容，经常可以获得有用的滤波器。该电路结构包括由“T”型电容(相当于“”型电容)分隔的并联电感。所有电容都通过实验进行调整，以获得满意的(不一定是最佳的)滤波器特性。这些滤波器适用于通带相当窄且不需要非常平坦的情况，以及阻带不需要太靠近通带就能给出非常高损耗的情况。使用更少元件的同样令人满意的设计可能是可能的，但可能不值得更大的设计和调整努力。“调整”设计和“理想”设计之间的性能差异可能会随着调谐电路数量的增加而非常迅速地增加。

插入损耗滤波器理论为我们提供了一些关于调整滤波器可能性的见解。假设通带相当窄。除了滤波器两端的电感外，所有电感在一定范围内可以具有任何值，而外部滤波器特性不会改变。这是因为电容可以被调整以产生等效的理想阻抗变压器(每诺顿)。具有最大零损耗实频数的插入损耗滤波器(非耗散和)需要在滤波器两端具有相等的电感(对于相等的终端电阻)。如果两个终端电感与设计值有相同的微小差异，则可以调整滤波器的带宽。对应于稍微不相等的终端电感，将有包括附加恒定损耗的插入损耗设计。问题不在于存在用于插入损耗特性的电容调整，而在于如何找到调整。

模拟滤波器理论在数字滤波器中的应用取决于数字滤波器的性质。模拟逼近理论可以直接应用于无限冲激数字滤波器(“”的有理函数)，通过双线性变换实现。但是双线性变换通常不适用于有限冲激响应滤波器(中的多项式)。最大平坦度、切比雪夫通带或阻带以及椭圆滤波器的概念仍然适用，但应用更加困难。此外，对于有限冲激响应(FIR)滤波器，还有不同的各具优势的概念和技术，特别是傅里叶级数和“加窗”。

今后

在我们日益数字化的未来，我们的滤波器中无疑将有越来越大的一部分是数字的。对于许多模拟滤波器而言，在、转换器之间使用数字滤波器可能会变得越来越经济，集成在单个芯片上。也许这类可编程滤波器中的少数几个将取代许多单独设计的滤波器，就像微处理器在其他应用中所占据的主导地位一样。但是，根据频率范围、滤波器要求、信号性质、要制造的单位数量等，某些用途肯定仍然需要模拟滤波器。

在过去的半个多世纪里，网络综合与滤波器理论的诞生与成长，已然成为诸多探索者心中一段弥足珍贵的历程。这一历程不仅丰富了我们的知识体系，更对电子学的演进产生了深远的影响。我有幸涉足通信工程这一领域，虽说是机缘巧合，但谁又能料到，这一选择竟能引领我见证并参与电子学所带来的技术与社会革命。回望过去，我们不难发现，每一次理论的突破与实践的创新，都在推动着人类文明不断向前。

REFERENCES

[1] V. Belevitch, "Summary of the history of circuit theory," Proc. IRE, vol. 50, no. 5, pp. 848-855, May 1962.
[2] R. M. Foster, Telephone conversations, May 11 and June 9, 1983. Letter June 3, 1983
[3] P. J. Nahin, "Oliver Heaviside, genius and curmudgeon," IEEE Spectrum, vol. 20, no. 7, pp. 63-69, July 1983.
[4] R. M. Foster, "Academic and theoretical aspects of circuit theory," Proc. IRE, vol. 50, no. 5, pp. 866-871, May 1962.
[5] S. Darlington, "A survey of network realization techniques," IRE Trans. Circuit Theory, vol. CT-2, pp. 291-297, Dec. 1955.
[6] G. Szentirmai, "Synthesis of multiple-feedback active filter," Bell Syst. Tech. J., vol. 152, no. 4, Apr. 1973; see first sentence, p. 527.
[7] G. A. Campbell, Collected Papers of George A. Campbell. New York: AT&T Co., 1937. Introduction by E. H. Colpitts: pp. 1-9. Loaded Lines: pp. 2-5 and 10-39. 4-Ports of Ideal Transformers: pp. 119-168.
[8] S. Darlington, "Some thoughts on the history of circuit theory," IEEE Trans. Circuits Syst., vol. CAS-24, no. 12, pp. 665-666, Dec. 1977.

[0]:已故作者曾在美国新罕布什尔州达勒姆市新罕布什尔大学电气与计算机工程系工作，邮编03824。
这是IEEE TRANSACTIONS ON Circuits and Systems，vol. CAS-11，pp. 1-13，1984年1月发表的一篇论文的再版。
出版商项目标识符S 1057-7122(99)00537-1。
[1]:根据坎贝尔多年前给福斯特的两封内部AT&T信件的(可能不完美的)副本。
[2]:向桑顿·怀尔德道歉。在他的小说《The Eighth Day》中，他用类似的术语将人与事件之间的相互关系比作挂毯。
[3]:由于这项发明，斯蒂比茨最近被选入“National Inventor's Hall of Fame”。
[4]:我是通过参与一些太空项目了解到霍曼转移椭圆的。它可能包含在霍曼1925年的一本德国书中，在C. C. Adams的《Space Flight》一书中提到，New York, McGrawHill, 1958, p. 18.

审核编辑：黄飞