

信号无失真传输的好帮手—相位线性度测试
描述
相位线性度在通信系统中起着至关重要的作用,就像音符在音乐中的重要性一样。在音乐中,音符的顺序和时间决定了旋律的和谐和优美。同样地,相位线性度决定了信号传输的准确性和可靠性。如果系统的相位线性度不佳,就像音乐中的音符不准确或混乱一样,会导致接收的信息失真。
现代移动通信、卫星通信等系统中广泛采用了相位调制体制,如QPSK、QAM等数字调制技术,器件的相位非线性会引起系统带内相位关系的变化,使调制信号失真。尤其使用高阶QAM调制的通信系统,其相位误差的敏感度更高, 这使得系统的相位线性度成为一个绕不开的话题。
什么是相位线性度?
相位线性度就是信号经系统传输后,实际相位与理想相位的偏差。
想要深入理解这个概念,我们就需要从《信号与系统》的无失真传输条件说起:
奥本海姆老先生在“线性时不变系统频率响应的模和相位表示”这一章节中,以理想频率选择性滤波器引出:要满足“波形不失真传输”,系统需同时满足两个条件
条件1:幅度/频率特性在工作频率范围内要保持恒定;
条件2:相位/频率特性在工作频率范围内保持线性,传输群时延保持恒定,不随工作频率而变化。
为了更好的帮助大家理解这两个条件,接下来以一个方波通过一个带通滤波器为例,来描述信号传输过程中的变化。
在《信号与系统》中,我们可以了解到方波信号包含基波、三次谐波、五次谐波等频率成分。假设这些频率成分都在这个滤波器的工作频率范围内,根据图2我们可以得出:信号经过这个滤波器后,只是幅度变小,有一定的延迟,但信号的形状仍是方波,周期也没变化。
也就是说, 如果一个器件带内幅频特性是常量且相频特性为线性,信号经由它传输,不会失真。
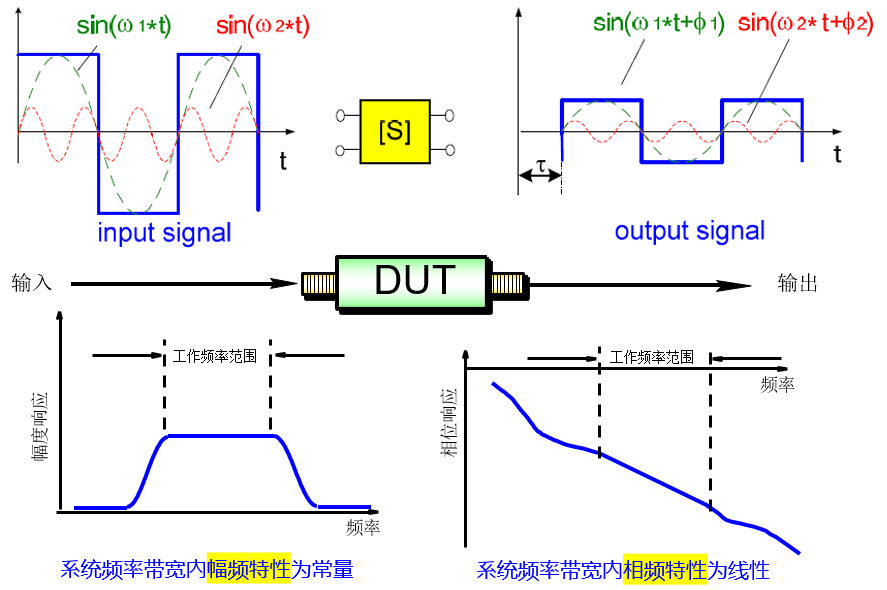
图 2 无失真传输条件
所以:理想的系统带内幅频特性是常数;相频特性具备线性特征;群时延是常数;频带内传输信号不会产生失真。
而实际器件的相频特性与理想的线性相位相比,有一定偏差,群时延随频率有一定波动。衡量器件相位线性程度的两个主要参数为群时延纹波和相位线性度。
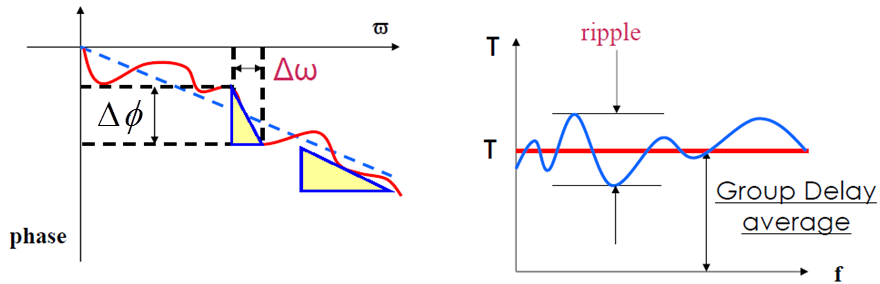
图 3 相位线性度是被测件实际相频响应与理想线性相位的偏差(左),群时延纹波也可反映相位的线性度(右)
对于高阶QAM调制的通信系统,相位误差的敏感度更高。相位失真会导致信号质量下降,增加误码率,甚至可能导致通信中断。为了确保信号的准确传输和解调,系统的相位线性度测试至关重要。
相位线性度该如何测得呢?
传统方法:利用群时延纹波来计算相位线性度
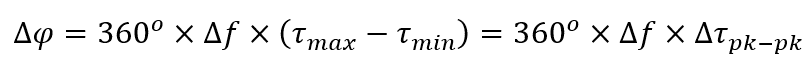
其中,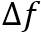 为群时延孔径(aperture),
为群时延孔径(aperture),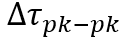 是群时延纹波的峰峰值。
是群时延纹波的峰峰值。
测试案例:
使用R&S公司的ZNA矢量网络分析仪,测一个中心频率 8 GHz,带宽 8 GHz的器件,测试条件是SPAN = 8 GHz,扫描1001个点,群时延孔径取20,测得群时延波动 35.8ps。
使用公式计算得到相位线性度:
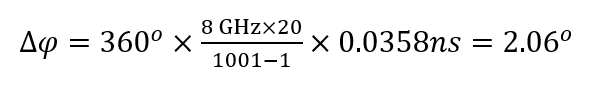
实际上,这种方法通过测群时延纹波求得相位线性度,有较大的不确定度,孔径选择对测量结果也有一定影响。孔径选取过小,会带来噪声波动,孔径过大,会遗漏变化细节。如何设置,业界并无统一规则,常常让工程师们手足无措。
R&S的矢量网络分析仪具有强大的功能,可以为相位线性度测试提供三种新方法。
新方法01
Trace中统计功能的妙用
步骤
这种方法实际上是用start和stop两端频点的相位确定理想的相频特性,确定一条直线,Flatness就是实测迹线偏离理想相频特性的峰峰值。
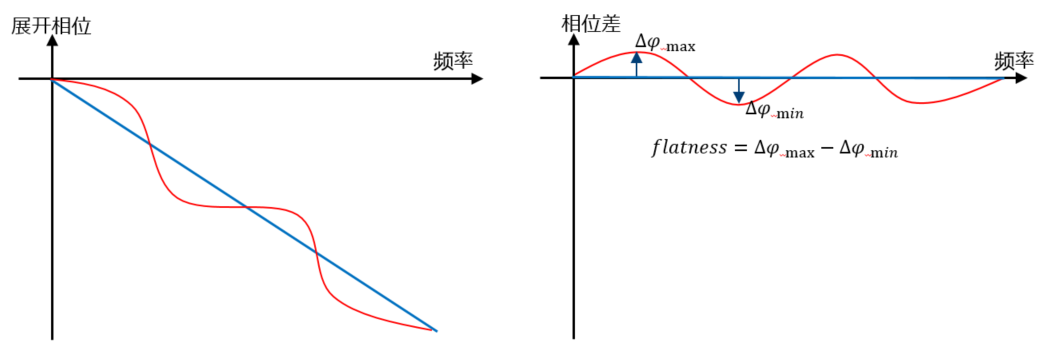
图 4 Trace中统计功能计算相位线性度的原理
新方法02
Auto Length计算相位线性度
步骤
Auto Length(也称 “自动长度检测” )计算扫描范围的平均电长度,通过参考面的平移,将各测试频点补偿同一个常数群时延。再通过Trace统计里的pk-pk读出相位线性度。
利用测试案例中提到的器件,测得的相位线性度为2.48°,与传统方法测得(2.06°)有一定差异。
新方法03
Trace中线性偏差应用
步骤
R&S ZNA矢量网络分析仪针对相位线性度测试,设计了Linearity Deviation快捷菜单,它用线性回归算法。
假设DUT的相位特性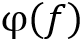 可表示为自变量
可表示为自变量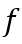 的线性组合
的线性组合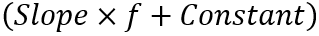
,加上一个随机误差项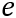 。其中
。其中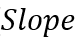 是斜率,
是斜率,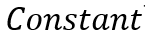 是截距:
是截距:
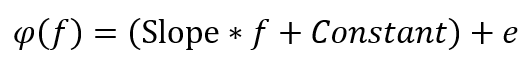
我们的目标是根据实测相位(unwrap phase)曲线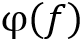 ,找到合适的
,找到合适的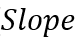 和
和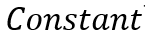 ,使得误差项
,使得误差项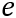 的平方和最小。
的平方和最小。
这时,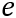 就是实测相位与拟合相位的偏差,而偏差的峰峰值就是相位线性度。
就是实测相位与拟合相位的偏差,而偏差的峰峰值就是相位线性度。
下图利用R&S的ZNA矢量网络分析仪测得结果为2.43°。
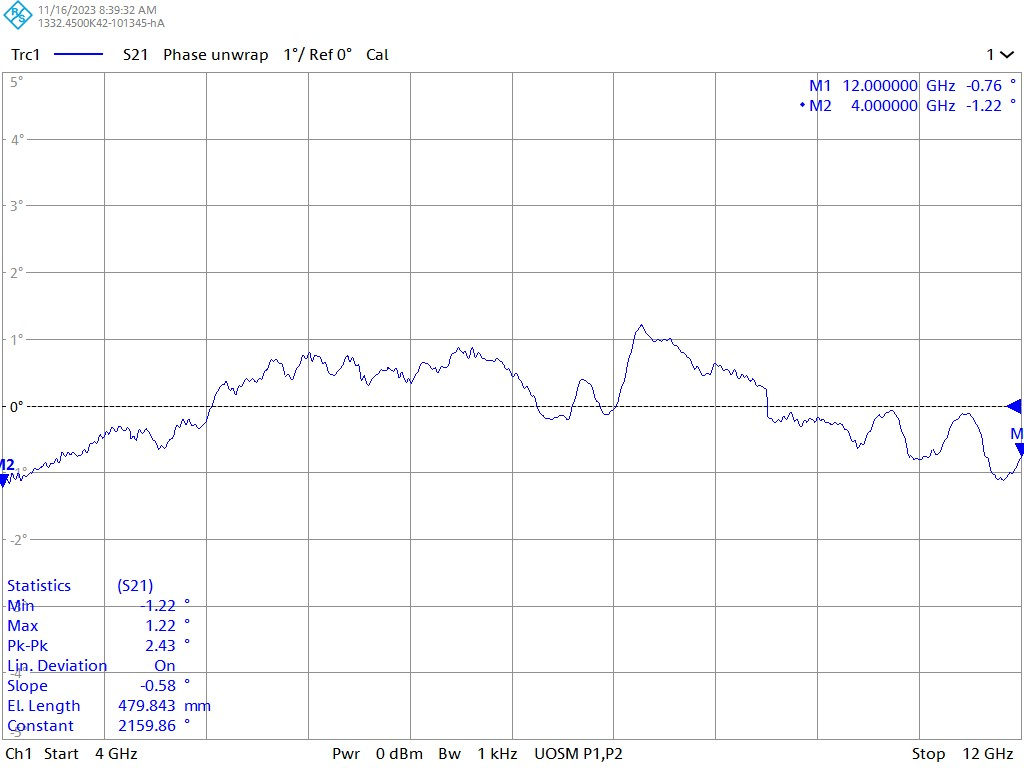
图 6 利用Trace功能中线性偏差的实测结果
方法3既避免了传统方法中选择群时延孔径的烦恼,也避免了方法1中只用了开始频点相位、终止频点的相位参与计算导致相频特性的不精确。此外,方法2中通过AutoLength补偿平均群时延值的操作繁琐,也涉及到选择群时延孔径的烦恼。
推荐小伙伴们使用LinearityDeviation法, 因为被测件全带宽内每个频点都参与线性回归计算,使得误差项的平方和最小,拟合出来的相位特性更接近被测件真实特性。
审核编辑:刘清
-
正弦波低失真度测试仪功能特点 音频信号分析仪 失真度仪2025-05-07 777
-
设计的无源带通滤波器,不同频率的信号会产生不一样的相位偏移, 导致输出信号失真怎么解决?2024-08-14 656
-
解读Tx/Rx系统中的非线性失真2023-09-05 3656
-
新唐参考应用|KVM无缝切换多台计算机的好帮手2023-08-11 1377
-
[6.4.1]--无失真传输系统jf_90840116 2022-12-11
-
#硬声创作季 信号与系统:4-8-1-2线性系统不失真传输信号的条件(2)Mr_haohao 2022-10-31
-
相位失真是什么意思_如何解决相位失真2019-09-26 18582
-
【MDP-XP数字电源申请】物联网项目好帮手MDP-XP迷你数字电源2019-08-27 1842
-
偏离线性相位程序错误地表征了DUT2019-08-23 2149
-
线材测径仪测量轧材的好帮手2018-11-27 2525
-
信号无失真传输的条件_无失真传输的条件2018-03-19 132310
-
初学者好帮手,EMC基础知识详细介绍(103页PPT)2015-08-17 17418
-
好帮手电子争取两年内上市2009-12-15 919
全部0条评论

快来发表一下你的评论吧 !

