简析控制系统的稳定性判据

本期内容                  

上一篇视频，我们已经对控制系统分析的关键 —— 传递函数进行了深入浅出的介绍（点我穿越回上一期内容）。

本期视频则基于前述概念，简析控制系统的稳定性判据。

01通常，对控制系统的分析主要有两种思路：

时域分析法  

即观察一段时间内，系统输出跟随输入的响应关系。通常会考虑根据系统的微分方程或传递函数、以拉氏变换为数学工具求解，依据响应曲线来分析系统性能。这种方法相对直观，但数学模型的建立较难。

频域分析法  

转换思路到频域进行处理。

因为系统频率特性可通过实验测定，并且频率特性本身也能够反映系统的传递函数，因此在实际操作中频域分析法对控制系统的分析和设计有着相对更强的实践意义。 其中图解法是分析控制系统频率响应的经典手段，而最为著名的两种方法就是以奈奎斯特（Nyquist）命名的幅相特性曲线法和以伯德（Bode）命名的对数频率特性曲线法，二者均通过实验可测的控制系统开环传函频率响应特性来完成对系统稳定性的判断。

02由于伯德图在工程实践中应用更为广泛，所以今天我们将重点关注如何利用伯德图对控制系统进行稳定性判断。

首先，我们在此引入控制系统频率响应的概念：

即，系统对某一频率下正弦输入信号的稳态响应。

图 ：系统频率响应说明

分析求解可知，系统的稳态输出与输入之间具有同频、变幅、移相的关系。

而能够反映上述控制系统（或元件）对不同频率正弦输入信号的稳态频率响应特征的数学模型，即为系统的频率特性。因为频率特性属于传递函数的特例，其实质为定义在复平面(s平面)虚轴上的传递函数，将它写为复数形式后，可以看到该复数的模表征了系统的幅频特性、相角表征了系统的相频特性：

据此可知，通过向待测系统输入一个频率可变的正弦信号，且不断改变频率ω的取值，并测量与每一个ω值对应的稳态输出，记录相应频率下稳态输出与输入的幅值比和相角差，即可绘制幅值比与相角差随频率ω变化的曲线，从而求解幅频特性与相频特性表达式，这是一种非常直观且实践意义极强的系统特征分析方法。

而伯德提出的对数频率特性图解法，是将系统幅频特性与相频特性分别画在两个对数坐标系中进行分析，由一幅对数幅频曲线和一幅对数相频曲线合为完整的对数频率特性曲线：

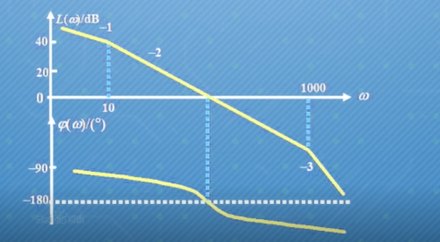
图 ：对数频率特性曲线 (伯德图) 

对数频率特性曲线的横坐标表示频率ω，并按对数分度十倍频程；

对数幅频曲线L(ω)的纵坐标表示对数幅频特性的函数值，即20lgA(ω)，线性均匀分度，单位是分贝，即幅频特性A(ω)每变化十倍，对数幅频特性L(ω)变化20dB；

对数相频曲线φ(ω)的纵坐标表示相频特性的函数值，线性均匀分度，单位是度或弧度。

选择在对数坐标系内分析，最直观的好处就是能够将表示控制系统内环节串联的幅频特性乘除运算转化为对数坐标系内的加减运算，从而简化曲线绘制；即系统的开环传递函数通常可以表示为若干个典型环节相乘形式，实际分析时就可以根据各频段下起主导作用的典型环节伯德图来直接完成系统开环伯德图的绘制。

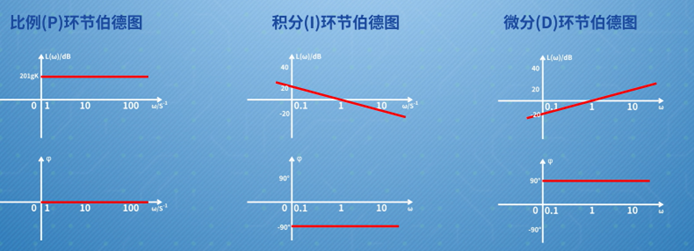
图 ：控制系统典型环节伯德图示意

03随着计算机辅助设计及仪器测量技术的发展，更多情况下，工程师朋友们面临的往往是根据仪器已经测得的伯德图来分析系统性能。

其中，频域性能指标最关键的参数就是稳定裕度：

稳定裕度可以定量地表征系统当前距离稳定边界(临界稳定)的远近，是评价系统稳定性好坏的性能指标，也是系统设计的重要依据之一。

良好的稳定裕度可以有效弥补分析设计过程中的简化处理或实际参数扰动等因素带来的偏差影响。

那么如何通过伯德图来判断系统的稳定裕度呢？

让我们回到最基本的控制系统判稳条件：系统稳定时，系统所有闭环极点(特征方程的根) 均具有负实部。

这意味着当系统不稳定时，特征方程的根具有正实部，即此时不稳定的闭环系统呈现不收敛的振荡发散状态，此时可认为稳态时闭环传递函数无穷大，从而可以推导得到系统开环传递函数G(s)H(s)=-1。

由此可以绘制开环传递函数为-1的系统伯德图，这就是系统处于临界稳定的边界：

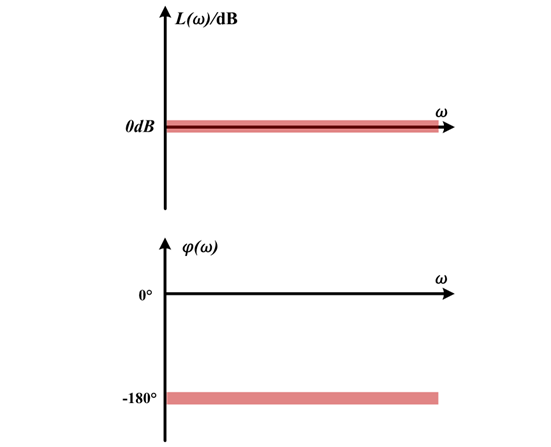
图 ：系统临界稳定时的伯德图

稳定裕度则代表实际控制系统的开环对数频率特性曲线距离幅频和相频稳定边界的远近，稳定裕度越高，意味着系统开环对数频率特性与稳定边界相去甚远，则系统抗扰性越好，在真实世界的各种外界扰动下更能实现稳定。

利用伯德图解法进行开环传递函数分析时，需要关注两个关键频率点：

定义ω_c为开环截止频率，这一频率点上系统幅频响应的幅值增益为1

定义ω_g为相角穿越频率，这一频率点上系统相频响应的相角为-180°

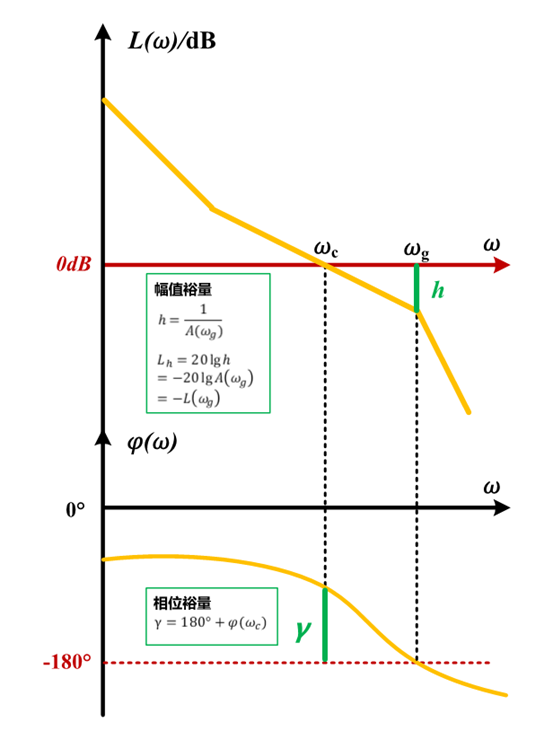
图 ：相位裕量与幅值裕量的定义

二者即为系统临界稳定时开环传函G(s)H(s)=-1所定义的边界。

定义相位裕量为γ=180°+φ(ω_C)，表征：

此时系统开环幅频特性不变的情况下，若相频特性再滞后γ度，系统将触碰稳定边界。

定义幅值裕量为h=1/(A(ω_g))，在对数频率特性坐标系中表示为L_h=20 lg⁡h=-20lgA(ω_g )=-L(ω_g)，表征：

此时系统开环相频特性不变的情况下，幅频特性再增大h倍，系统将触碰稳定边界。

一般相位裕量γ>0°理论上即可判断系统稳定，相位裕量越大则系统稳定程度越高，工程上一般要求设计时γ≥40°；

而幅值裕量h>1、对数幅值裕量L_h≥0dB时也可判断系统稳定，幅值裕量越大，系统稳定程度越高，类似地，工程上一般会在设计时要求保证L_h≥6dB (6-10dB)。

因此，对于一个控制系统来说，假如它能够实现在开环幅频特性穿越0dB线时带来的相位滞后少于-180°，或开环相频特性穿越-180°线时其开环幅频特性已经远低于0dB线，这样的对数幅频特性“穿越”才是表征系统稳定的可靠“穿越”。

04下面，我们来关注伯德图判稳在电源设计中的实际应用。

BODE100 环路分析仪可以辅助测量电源系统的伯德图，以MPQ4423C的评估板为例，进行伯德图的实测：

图 ：MPQ4423C环路测试示意

24V输入，5V输出带2A负载的情况下，MPQ4423C测得伯德图如图所示：

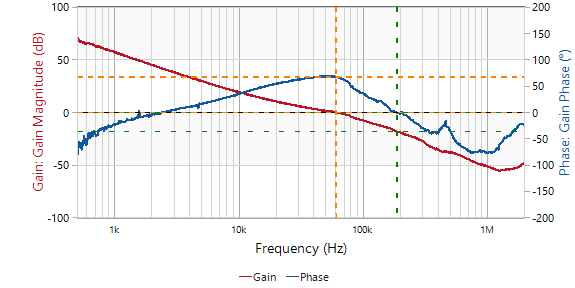
图 ：EVQ4423C环路测试结果

通过观察红色的幅频特性曲线与0dB线的交截点可以判断得到MPQ4423C的截止频率为60kHz； 而开环截止频率通常有个工程师更为熟悉的名字——带宽，表征系统的响应速度；带宽越高，意味着面对动态负载时系统输出跟随输入的响应能力越快。 由于BODE 100环路分析仪在做处理的时候，已将相频特性曲线整体抬升180°，故通过观察蓝色的相频特性曲线在截止频率下距离0°线的距离，即可直接得出系统的相位裕度为67.455°，意味着MPQ4423C有着相当优越的稳定性。       这一期的系统判稳就讲到这啦。

下一期我们会和大家探讨“环路参数具体该如何调节”，请大家持续关注电源小课堂后续视频！

审核编辑：汤梓红