RL究竟是如何与LLM做结合的？

RLHF 想必今天大家都不陌生，但在 ChatGPT 问世之前，将 RL 和 LM 结合起来的任务非常少见。这就导致此前大多做 RL 的同学不熟悉 Language Model（GPT）的概念，而做 NLP 的同学又不太了解 RL 是如何优化的。在这篇文章中，我们将简单介绍 LM 和 RL 中的一些概念，并分析 RL 中的「序列决策」是如何作用到 LM 中的「句子生成」任务中的，希望可以帮助只熟悉 NLP 或只熟悉 RL 的同学更快理解 RLHF 的概念。

1. RL: Policy-Based & Value Based

强化学习（Reinforcement Learning, RL）的核心概念可简单概括为：一个机器人（Agent）在看到了一些信息（Observation）后，自己做出一个决策（Action），随即根据采取决策后得到的反馈（Reward）来进行自我学习（Learning）的过程。

光看概念或许有些抽象，我们举个例子：现在有一个机器人找钻石的游戏，机器人每次可以选择走到相邻的格子，如果碰到火焰会被烧死，如果碰到钻石则通关。

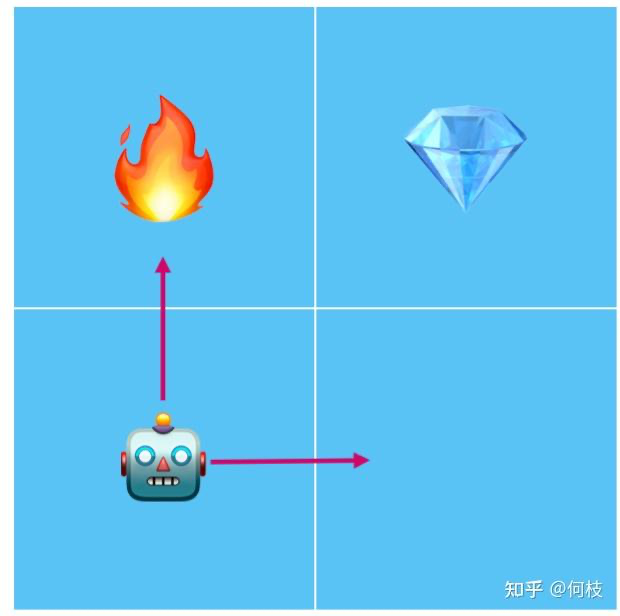
机器人找钻石的例子：碰到火焰则会被烧死

在这个游戏中，机器人（Agent）会根据当前自己的所在位置（Observation），做出一次行为选择（Action）：

如果它此时选择「往上走」，则会碰到火焰，此时会得到一个来自游戏的负反馈（Reward），于是机器人会根据当前的反馈进行学习（Learning），总结出「在当前的位置」「往上走」是一次错误的决策。

如果它此时选择「向右走」，则不会碰到火焰，并且因为离钻石目标更近了一步，此时会得到一个来自游戏的正反馈（Reward），于是机器人会根据当前的反馈进行学习（Learning），总结出「在当前位置」「往右走」是一次相对安全的决策。

通过这个例子我们可以看出，RL 的最终目标其实就是要让机器人（Agent）学会：在一个给定「状态」下，选择哪一个「行为」是最优的。

一种很直觉的思路就是：我们让机器人不断的去玩游戏，当它每次选择一个行为后，如果这个行为得到了「正奖励」，那么下次就多选择这个行为；如果选择行为得到了「负惩罚」，那么下次就少选择这个行为。

为了实现「多选择得分高的行为，少选择得分低的行为」，早期存在 2 种不同的流派：Policy Based 和 Value Based。

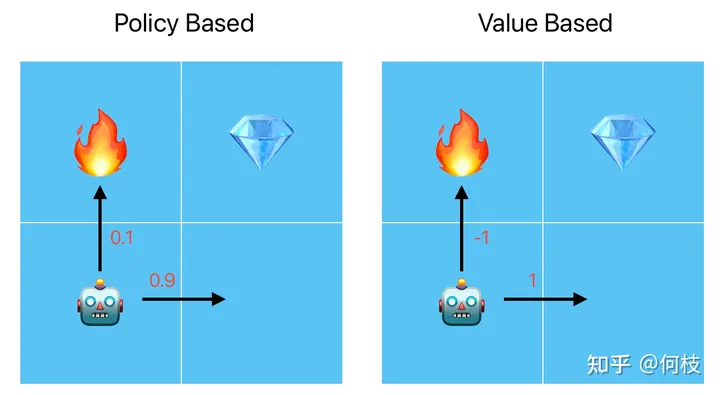
Policy Based 将行为量化为概率；Value Based 将行为量化为值

其实简单来说，这 2 种流派的最大区别就是在于将行为量化为「概率」还是「值」，具体来讲：

Policy Based：将每一个行为量化为「概率分布」，在训练的时候，好行为的概率值将被不断提高（向右走，0.9），差行为的概率将被不断降低（向上走，0.1）。当机器人在进行行为选择的时候，就会按照当前的概率分布进行采样，这样就实现了「多选择得分高的行为，少选择得分低的行为」。

Value Based：将每一个行为量化为「值」，在训练的时候，好行为的行为值将被不断提高（向右走，1分），差行为的行为值将被不断降低（向上走，-1）。当机器人在进行行为选择的时候会选择「行为值最大的动作」，这样也实现了「多选择得分高的行为，少选择得分低的行为」。

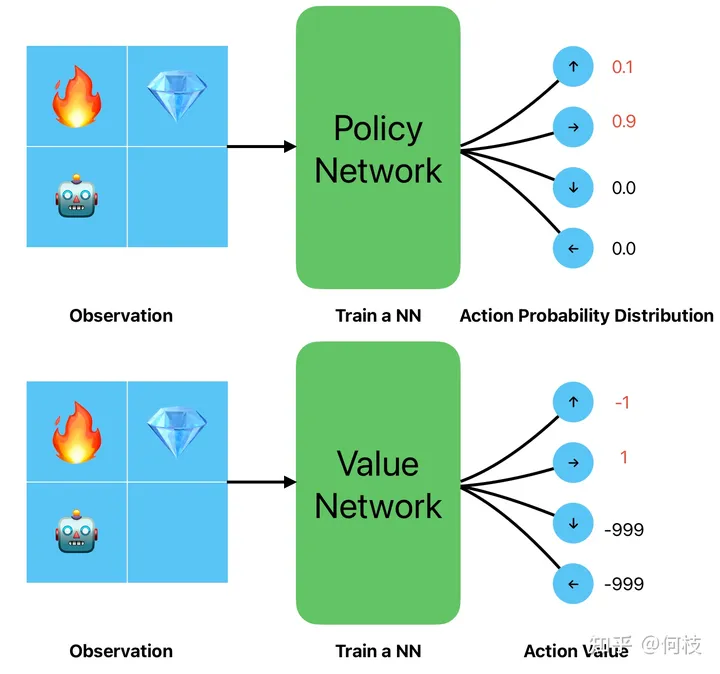
两种策略输入一样，只是输出的形式不一样（概率 v.s. 值）

关于这 2 种流派的更多训练细节在这里就不再展开，如果感兴趣可以看看比较出名的代表算法：[Policy Gradient]（Policy Based）和 [Q-Learning]（Value Based）。

讲到这里，我们可以思考一下，Language Model（GPT）是属于 Policy Based 还是 Value Based ？

为了弄明白这个问题，我们下面一起看看 GPT 是怎么工作的。

2. Language Model（GPT）是一种 Policy Based 还是一种 Value Based？

GPT 是一种 Next Token Prediction（NTP），即：给定一段话的前提下，预测这段话的下一个字是什么。

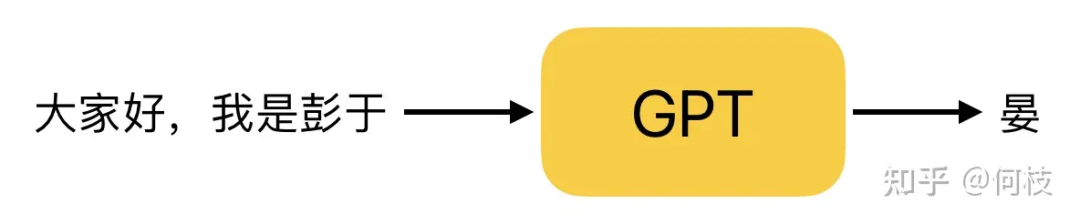
GPT 工作原理（Next Token Prediction，NTP）

而 GPT 在进行「下一个字预测」的时候，会计算出所有汉字可能出现的概率，并根据这个概率进行采样。

在这种情况下，我们完全可以将「给定的一段话」看成是我们上一章提到的 Observation，

将「预测的下一个字」看成是上一章提到的 Action，而 GPT 就充当了其中 Agent 的角色：

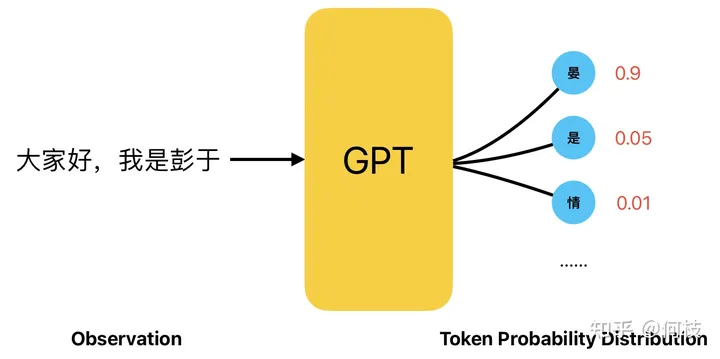
GPT 生成文本的过程，一个典型的 Policy Based 过程

如此看来，Language Model 的采样过程其实和 Policy Based 的决策过程非常一致。

回顾一下我们之前提到过 RL 的目标：在一个给定「状态」下，选择哪一个「行为」是最优的，

迁移到 GPT 生成任务上就变成了：在一个给定的「句子」下，选择（续写）哪一个「字」是最优的。

因此，将 RL 中 Policy Based 的训练过程应用到训练 GPT 生成任务里，一切都显得非常的自然。

通过 RL 对 GPT 进行训练，我们期望 GPT 能够学会如何续写句子才能够得到更高的得分，

但，现在的问题是：游戏中机器人每走一步可以通过游戏分数来得到 reward，GPT 生成了一个字后谁来给它 reward 呢？

3. 序列决策（Sequence Decision）以及单步奖励（Step Reward）的计算

在第一章和第二章中，我们其实讨论的都是「单步决策」：机器人只做一次决策，GPT 也只生成一个字。

但事实上，机器人想要拿到钻石，通常需要做出 N 次行为选择。

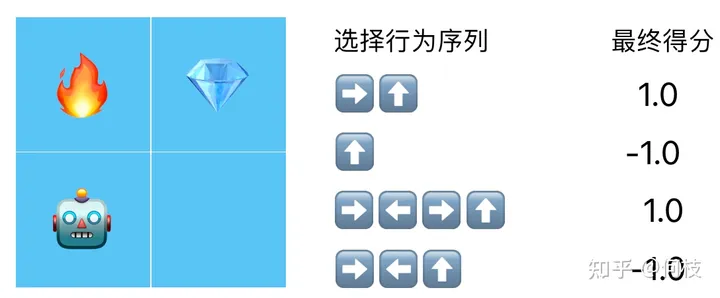
不同的行为选择序列得到的得分：假设拿到 得1分，碰到 得-1分，其余情况不加分也不扣分

在这种情况下我们最终只有 1 个得分和 N 个行为，但是最终 RL 更新需要每个行为都要有对应的分数，

我们该如何把这 1 个总得分对应的分配给所有的行为呢？

答案是计算「折扣奖励（discount reward）」。

我们认为，越靠近最末端的行为对得分的影响越大，于是从后往前，每往前行为就乘以 1 次折扣因子 γ：

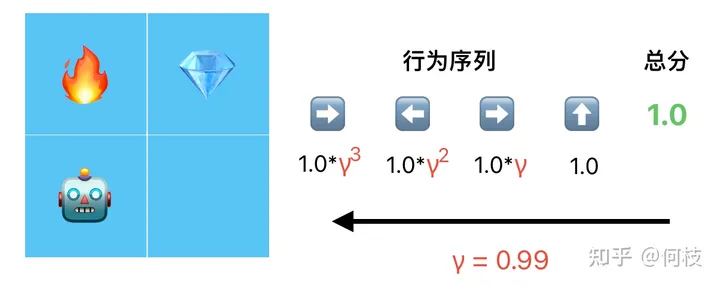
根据最终得分（total reward），从后往前倒推出每一个行为的得分（step reward）

同样，GPT 在生成一个完整句子的过程中，也会做出 N 个行为（续写 N 个字），

而我们在评分的时候，只会针对最后生成的完整句子进行一个打分（而不是生成一个字打一个分），

最后，利用上述方法通过完整句子的得分倒推出每个字的对应得分：

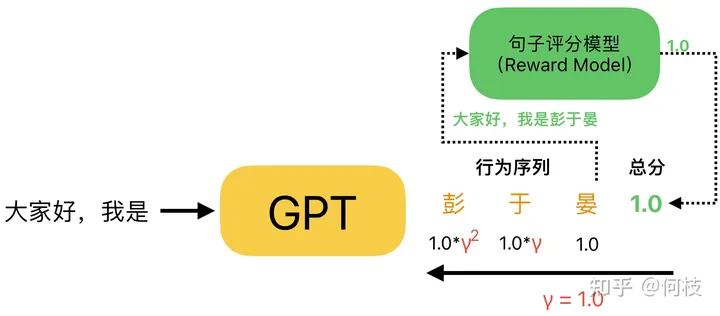
注意：在 GPT 的得分计算中，通常折扣因子（γ）取 1.0

值得注意的是：通常在对 GPT 生成句子进行得分拆解的时候，折扣因子（γ）会取 1.0，

这意味着，在句子生成任务中，每一个字的生成都会同等重要地影响着最后生成句子的好坏。

我们可以这么理解：在找钻石的游戏中，机器人采取了一些「不当」的行为后是可以通过后续行为来做修正，比如机器人一开始向右走（正确行为），再向左走（不当行为），再向右走（修正行为），再向上走（正确行为），这个序列中通过「修正行为」能够修正「不当行为」带来的影响；但在句子生成任务中，一旦前面生成了一个「错别字」，后面无论怎么生成什么样的字都很难「修正」这个错别字带来的影响，因此在文本生成的任务中，每一个行为都会「同等重要」地影响最后句子质量的好坏。

4. 加入概率差异（KL Penalty）以稳定 RL 训练

除了折扣奖励，在 OpenAI 的 [Learning to summarize from human feedback] 这篇工作中指出，

在最终生成句子的得分基础上，我们还可以在每生成一个字时候，计算 RL 模型和 SFT 模型在生成当前字的「概率差异」，并以此当作生成当前字的一个 step reward：

通过概率差异（KL）作为 reward 有 2 个好处：1. 避免模型崩溃到重复输出相同的一个字（模式崩溃）。2. 限制 RL 不要探索的离一开始的模型（SFT）太远

通常在进行 RL 训练时，初始都会使用 SFT 模型做初始化，随即开始探索并学习。

由于 RL 的训练本质就是：探索 + 试错，

加上「概率差异」这一限制条件，就相当于限制了 RL 仅在初始模型（SFT）的附近进行探索，

这就大大缩小了 RL 的探索空间：既避免了探索到那些非常差的空间，又缓解了 Reward Model 可能很快被 Hacking 的问题。

我们举一个具体的例子：

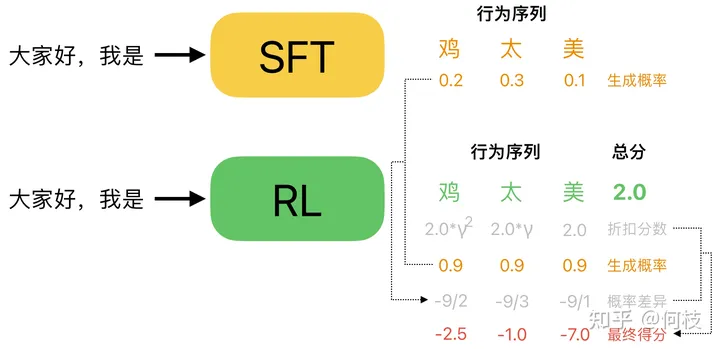
加上 KL 惩罚（概率差异）约束后的 step reward

如上图所示，对于「大家好，我是」这个 prompt，Policy（RL）Model 认为「鸡太美」是一个很好的答案，

这可能是 Reward Model 打分不准导致的（这很常见），上图中 RM 给「鸡太美」打出了 2 分的高分（绿色）。

但是，这样一个不通顺的句子在原始的模型（SFT Model）中被生成出来的概率往往是很低的，

因此，我们可以计算一下「鸡太美」这 3 个字分别在 RL Model 和在 SFT Model 中被采样出来的概率，

并将这个「概率差异」加到 RM 给出的「折扣分数」中，

我们可以看到：尽管对于这个不通顺的句子 RM 给了一个很高的分数，但是通过「概率差异」的修正，每个字的 reward 依然被扣除了很大的惩罚值，从而避免了这种「RM 认为分数很高，但实则并不通顺句子」被生成出来的情况。

通过加入「概率差异」的限制，我们可以使得 RL 在 LM 的训练中更加稳定，防止进化为生成某种奇怪的句子，但又能「哄骗」Reward Model 给出很高分出的情况（RL 非常擅长这一点）。

但，如果你的 RM 足够的强大，永远无法被 Policy 给 Hack，或许你可以完全放开概率限制并让其自由探索。