

详解微电子器件的宏原型
电子说
描述
微电子模拟器件工作运行规律,对于初学者来言,看不见摸不着,理解起来难度大。针对这种情况,对于初学者有没有一种更好的理解方式呢?值得深思。纯属个人观念,微观世界与宏观世界是相对应的,若用宏观世界去理解微观世界,会更有利于对微观世界的理解和把握。因此,初学者在学习模拟器件工作运行规律时,可找个熟悉的宏观模型去类比,更好理解其工作运行规律,更好的去设计电路,分析解决电路的问题所在。
如图1所示,模拟集成电路设计中用到的器件可分为有源器件和无源器件两大类,有源器件常用的是三极管BJT、场效应管MOS;常用的无源器件有电容、电感、电阻、二极管和忆阻器。这些器件都可找到与其对应的宏观模型;需注意,所有类比的“宏原型”仅仅是为了方便理解和分析,不能完全的等效。
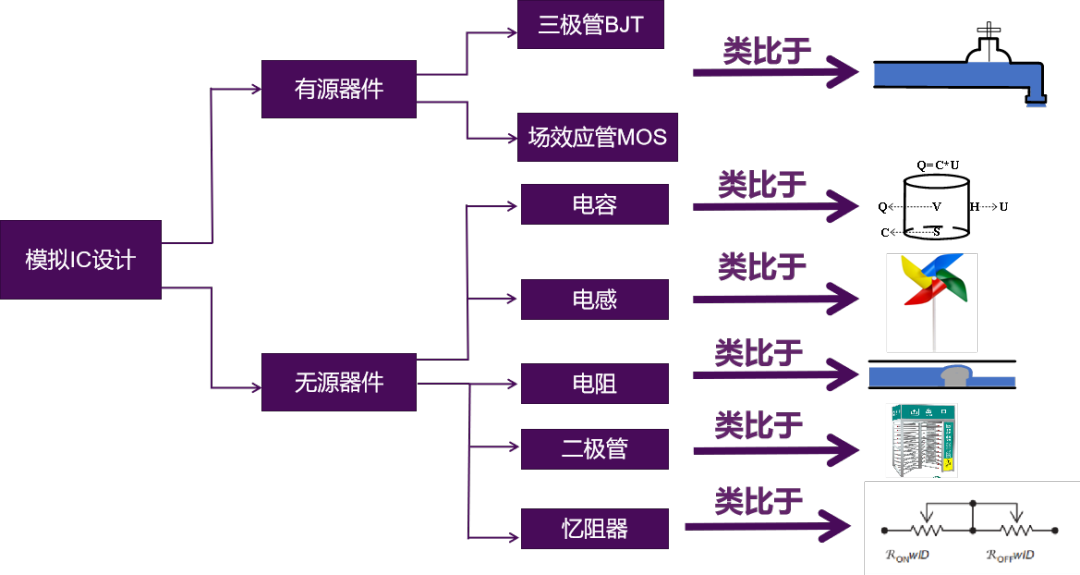
图1 模拟器件等效宏观模型
MOS管的宏原型:水龙头
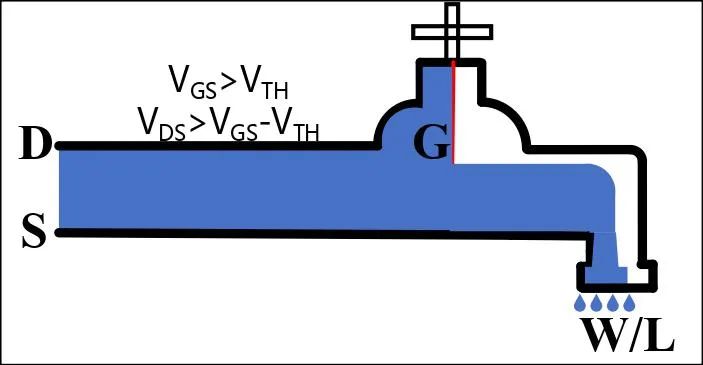
MOS管分为NMOS和PMOS两种,其两者在工作区分析中仅相差一个负号。因此,这里以NMOS为例,其模型对应的是宏观世界中带水龙头的水管,因不考虑MOS管的二级效应,忽略MOS管的衬底(B),如图2所示,NMOS管有三个极,栅极(G)、源极(S)、漏极(D)。假设流入水流的高度对应NMOS管的漏源电压(VDS),水龙头的阀门高度(后文简称阀门)对应NMOS的栅源电压(VGS),出水口对应NMOS管的宽长比(W/L)。这里以NMOS管的饱和区、线性区、截止区以及亚阈值区四个区进行解析说明。
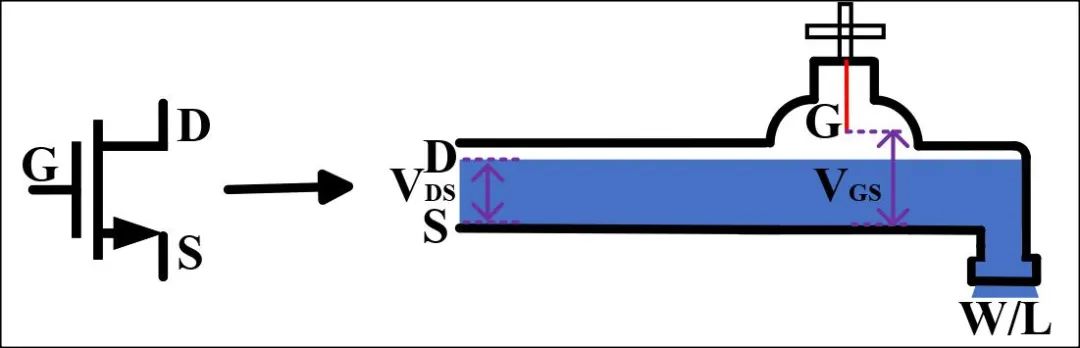
图2 NMOS管的等效宏观模型
工作在饱和区的NMOS管,在不考虑NMOS管的二级效应的前提下,如图3所示。图3(a)中,假设此时水龙头的阀门到水面的高度正好是VTH,该状态是NMOS管正好进入饱和区,此时NMOS管的输出电流达到最大值,对应水管的流出水流也达到最大。图3(b)中NMOS管进入一个深饱和区,此时流入的水流高度(VDS)高于阀门(VGS)的高度,不难发现,流出的水流大小(ID)主要受阀门(VGS)的高度影响,阀门的高度成为决定流出水流的关键因素,阀门高些,水流大些。同时,也会受出水口的大小(W/L)影响,出水口越大,单位时间流出的水越多。因此,饱和区的NMOS管电流公式如式1所示,主要是受VGS影响,同时也受W/L影响。
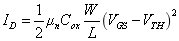
(1)
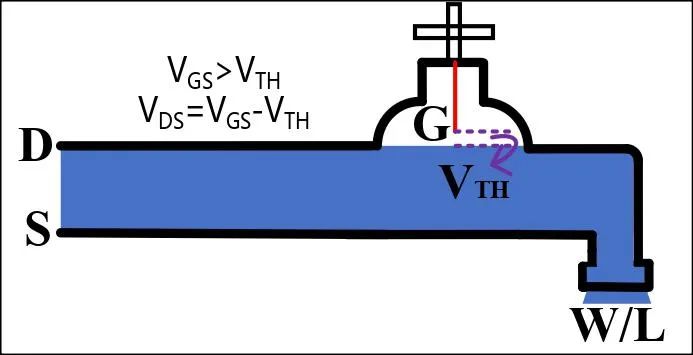
(a)
(b)
图3 NMOS管饱和区的宏观模型
工作在线性区的NMOS管,对应等效的宏观模型如图4所示,阀门(VGS)打开的很高,且流入的水流高度(VDS)低于阀门(VGS)减去一个电压阈值(VTH)。不难发现,前提是阀门(VGS)需要被打开且足够的高,该因素是影响水流流出大小的必要因素,不是主要因素,主要因素是水流流入的高度(VDS),因为,此时的水流流入是不会受到阀门的阻碍。同时,出水口(W/L)大小也是影响流出水流大小的因素,是次要因素。因此,NMOS管线性区的电流公式如式2所示,可看到VDS有两项,且其中一项是平方项,突出VDS是输出电流的主要因素。同时,式中还有VGS和W/L两项影响着输出电流大小。
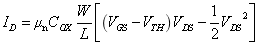
(2)
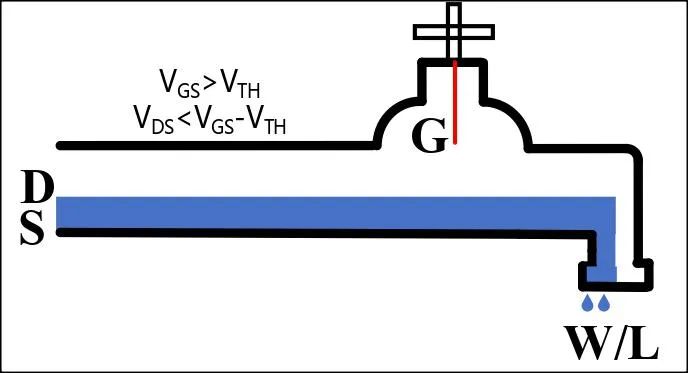
图4 NMOS管线性区的宏观模型
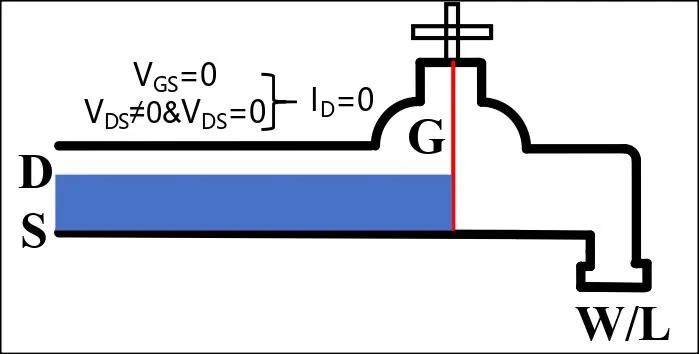
工作在截止区的NMOS管,对应等效的宏观模型如图5所示,只有两种情况才能认为NMOS管工作在截止区,第一种如图5(a),阀门关死(VGS=0),不管是否有水流流入(VDS取任意值),都不会有水流流出(ID=0);另一种如图5(b),无水流流入(VDS=0),不管阀门是否打开(VGS取任意值),也不会有水流流出(ID=0)。
(a)
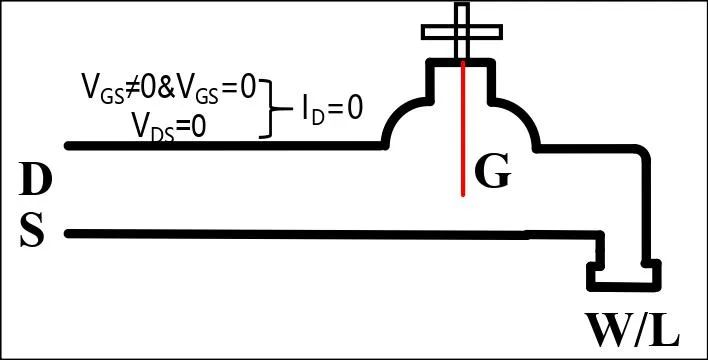
(b)
图5 NMOS管截止区的宏观模型
工作在亚阈值区的NMOS管,对应等效的宏观模型如图6所示,阀门未关死(VGS
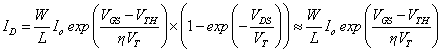
(3)
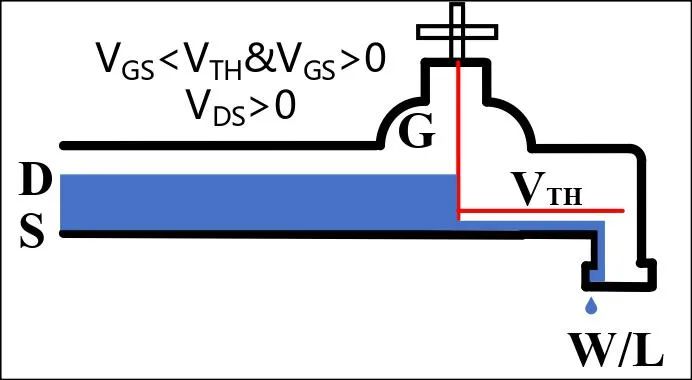
图6 NMOS管亚阈值区的宏观模型
三极管的宏观模型跟MOS管的宏观模型一样,这里就不赘述。
电容的宏原型:水桶
电容所对应宏观世界中的水桶(圆柱体)模型,如图7所示,圆柱体的底面积S等效为电容值C,圆柱体的高度H等效为该电容能承受的最大电压U,圆柱体的体积V等效为该电容的容值Q。为了形容电容的充放电,引入水龙头来模拟电容的充放电过程变化。
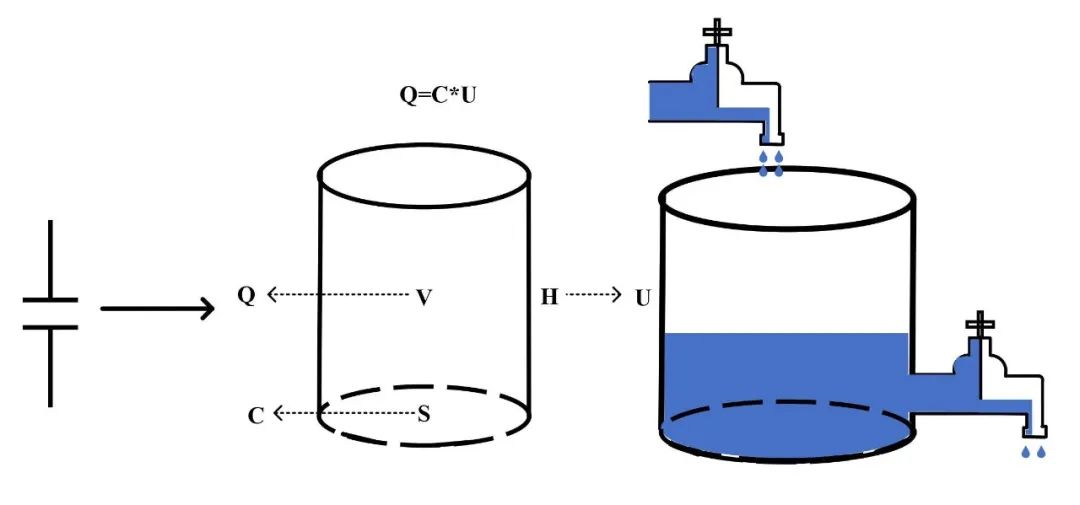
图7 电容的等效宏观模型
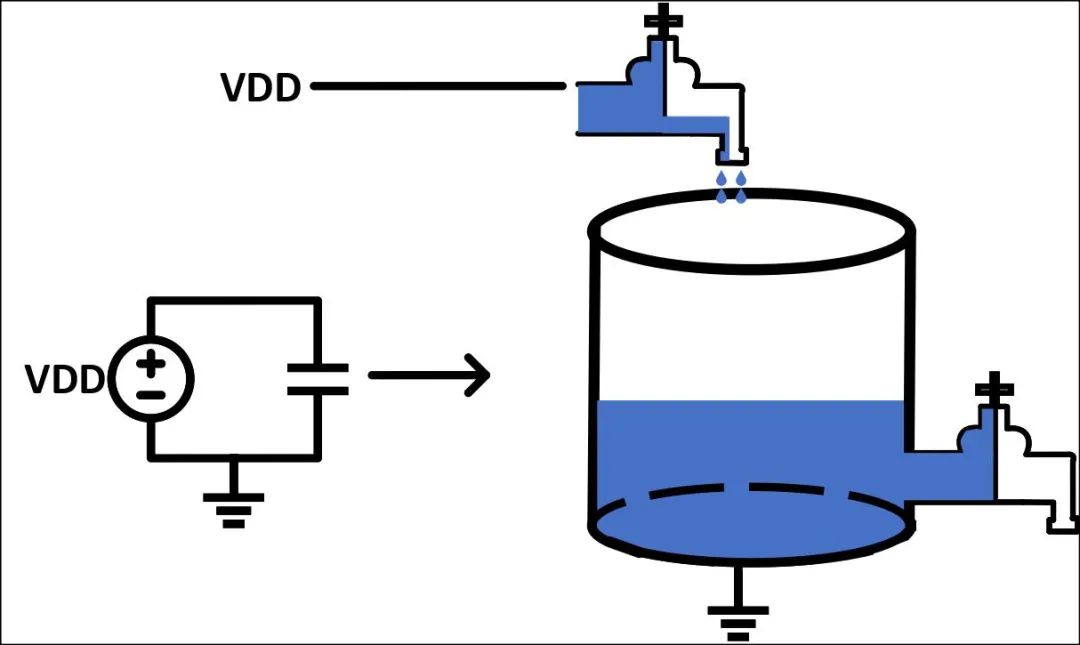
电容常见的三个性能分别是储能、滤波和升压,具体是怎么实现的呢?这时可以通过宏观的模型比较直观的看到电容的三个性能具体变化过程。首先来聊下,电容的储能和滤波,如图8所示。图8(a)中,在电容的两端接入一个直流电源,对电容进行充电,可以等效出圆柱体上面的水龙头打开,往圆柱体内灌水,圆柱体内的水面高度表现为电容上极板电平值,也可看作电容的输出电压。刚开始的时候,圆柱体内水面升的很快,这是因为水龙头流出的水到圆柱体的水面高度越高,水龙头流出水的水流速度越快,单位时间的水量越多,因此圆柱体内水面升的速度先快后慢(电容的充电过程是先快后慢),且圆柱体的下面水龙头没有打开(电容没有放电),那么圆柱体内的水会一直存储,这就是电容的储能过程。在电容的储能过程中,假设一直给电容充电,且该电容容值足够大,那么电容的输出电压会一直升高吗?答案当然不,正如当圆柱体的水面覆盖水龙头时,在两边的大气压强一样的情况下,水龙头的水是流不进去圆柱体内的。若是电容对外放电,此时圆柱体下面的水龙头打开,上面的水龙头关闭,下面水龙头流出的水流速度会随着圆柱体内的水面高度降低而减慢,这也解析了电容的放电过程也是先快后慢。
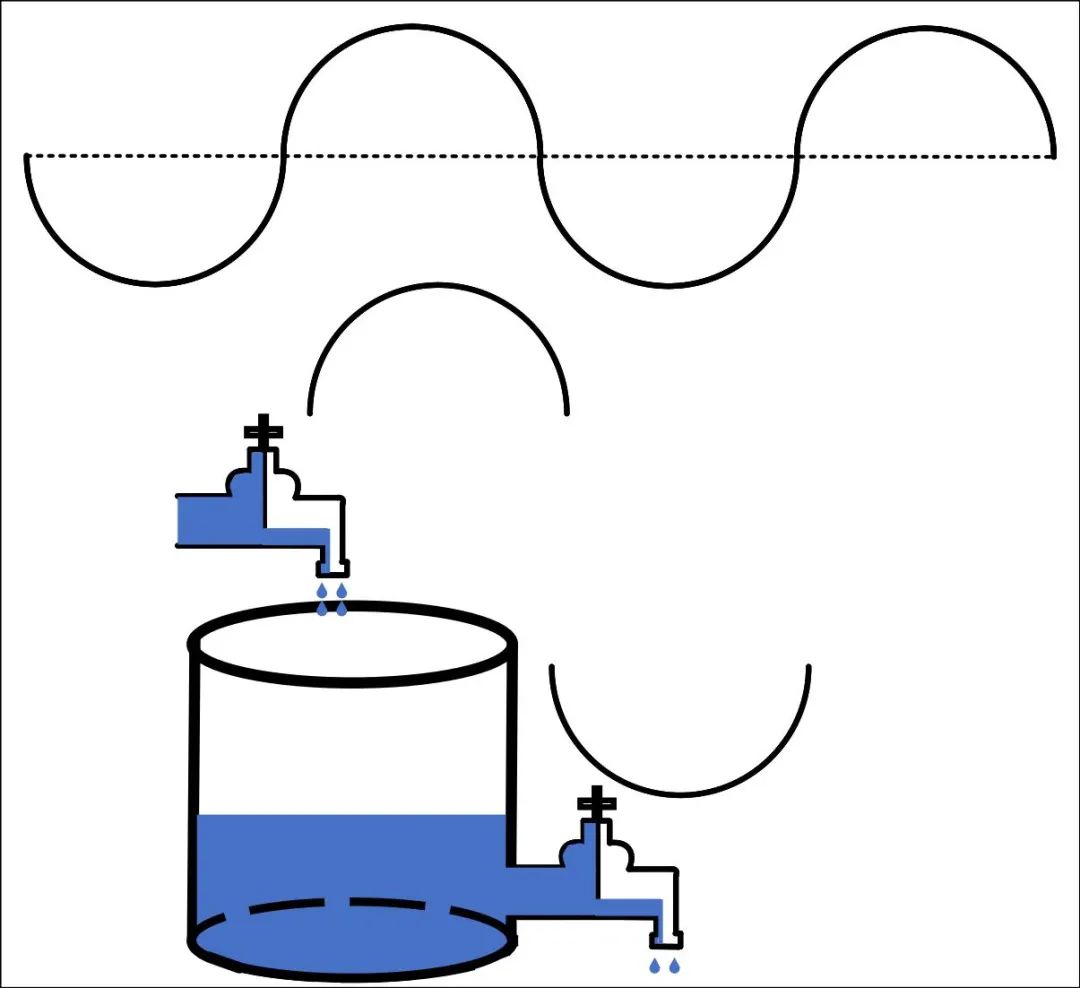
图8(b)中,是电容的滤波过程。总所周知,直流电的方向是不变的,要么正要么负;而交流电的方向是变化的,且都有一个相对零值,表现出正反之分,当为正时,对应圆柱体上面水龙头打开,为负时,对应圆柱体下面水龙头打开。假如输入图中的正弦波,正弦波正半部分对应圆柱体上面的水龙头打开,负半部分对应圆柱体下面的水龙头打开,这样流入的水量与流出的水量一致,那么圆柱体内的水的高度不变(电容输出电压不变),换句话说,电容的输出电容不会受到输入纹波的影响,这就是电容的滤波过程。
(a)储能过程
(b)滤波过程
图8 电容性能的宏观模型
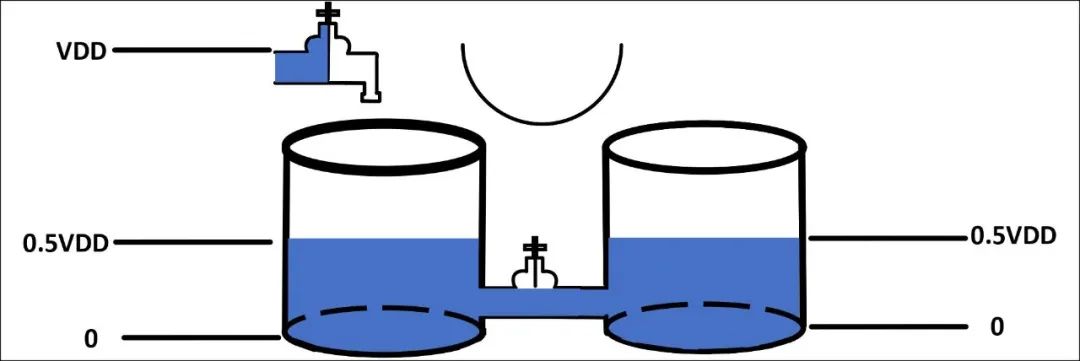
为了更直观的描述电容的升压过程,引入两个一样的电容宏观模型,如图9所示,分为三步。第一步先向第一个圆柱体灌满水,且水面高度为VDD(电容电压为VDD),底面(电容下级板)电平为零电平,则顶面(电容上极板)为VDD。第二步关闭上面水龙头的出水口(撤走输入电源),打开中间的阀门,两个圆柱体形成一个连通器,如图9(b)。在大气压强的作用下,两个圆柱体内水的高度会一样(电容电荷共享过程),右边的圆柱体的高度为0.5VDD(电容的电压为0.5VDD)。第三步关闭中间的阀门,右边的圆柱体的底面加个VDD电压,由于中间阀门关死,右边的圆柱体中的水流没法流出,水面高度保持不变(电容电压不变),此时右边圆柱体的水面高度为1.5VDD(电容的上极板抬高到1.5VDD),电容的输出电压为1.5VDD,完成电容的升压过程。
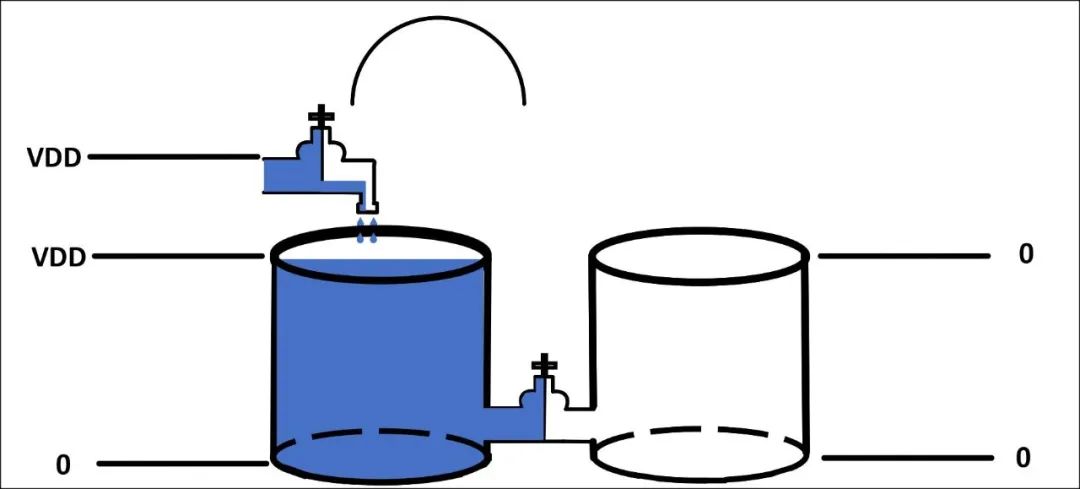
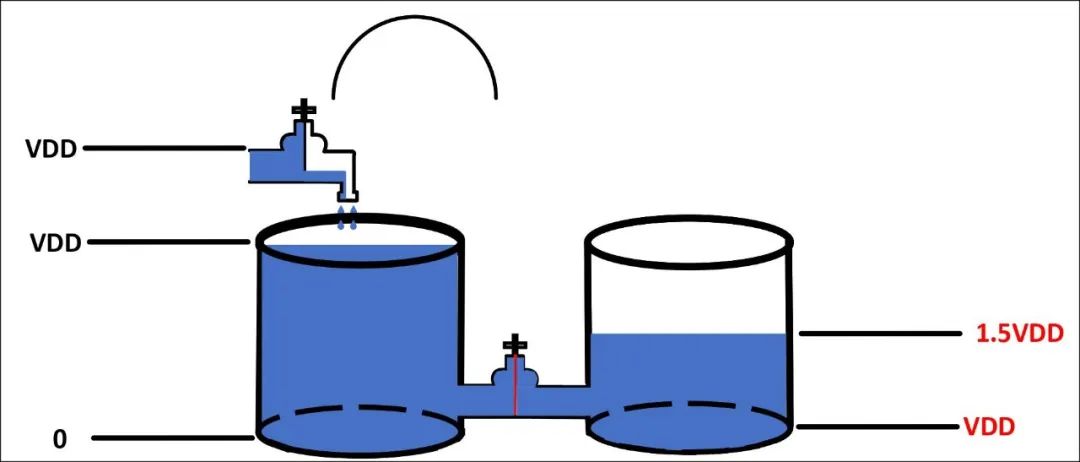
(a)第一步
(b)第二步
(c)第三步
图9 电容升压的宏观模型
电感的宏原型:风车
电感所对应宏观世界中的玩具风车模型,如图10所示。风车只有当有风吹动的时候,才能转动起来。不难发现,如果从两个相反的方向同时对着该玩具风车吹风的时候,风车是很难转动起来,但单方向吹风,风车就会很容易转动起来,这类似电感的通直阻交性能。记得小时候玩风车,吹一口气,风车只能维持一段时间的转动,这类似电感的短暂储能,若撤走输入电源,电感本身通过电生磁,在磁场中把自身储存的能量消耗殆尽。
图10 电感的等效宏观模型
电阻和二极管的宏原型:水管和单向旋转门
电阻所对应宏观世界中的堵塞水管模型,如图11(a)所示。水是从左流向右,则流入水的高度对应加在电阻两端的电压。图中灰色部分代表水管堵塞程度,所对应电阻的阻值大小。如图所示,10Ω的电阻比8Ω所对应的水管堵塞更严重,水流流过更困难,相同时间内,流出的水流更少,换言之,加在两个电阻的两端的电压值相同,电阻阻值越大的电阻所对应的电流值越小。同样,在同一个水管中,流入的水流越高(电阻两端电压值越大),水流越过堵塞物越容易,流出的水流越大(电阻的电流越大)。
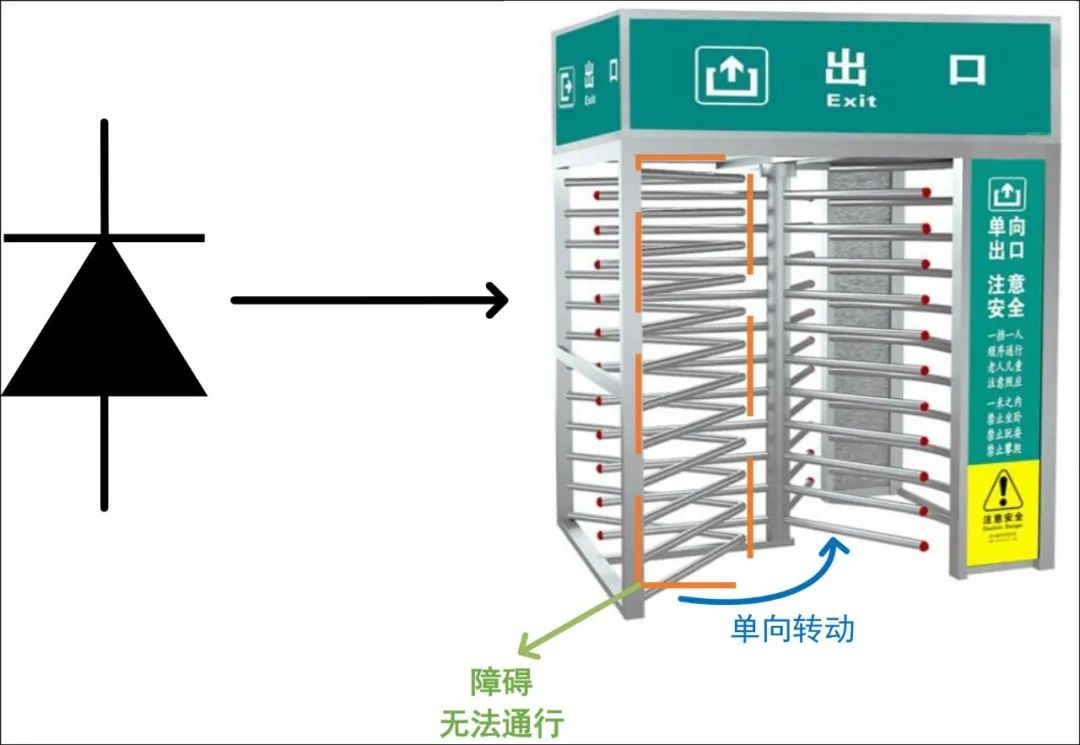
二极管所对应宏观世界中的单向旋转门模型,如图11(b)所示。火车站的出口以及一些写字楼的出口用的都是图11(b)中的单向旋转门,单向旋转门一侧有障碍,且只能单方向旋转。因此,单向旋转门只能在正向推力下才会转动;正向推力越大,转动的越快;无推力时就不会转动;且反向无法推动。其所表现出来的现象,分别对应二极管的单向导电性;正向电压大于二极管阈值电压就会无阻碍的导通,输入的电压越大,输出电压越大;无输入电压时,输出电压也无;加反向电压,二极管无法导通。
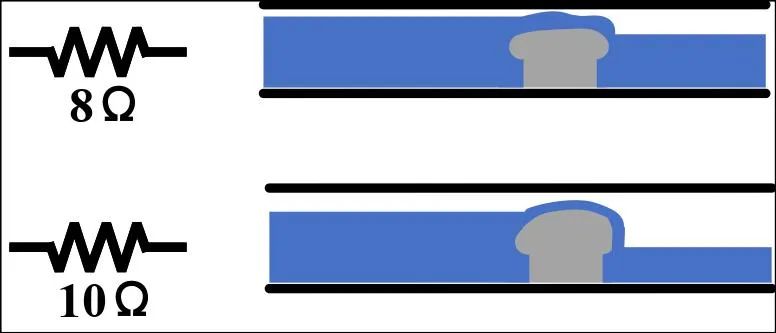
(a)电阻等效宏观模型
(b)二极管等效宏观模型
图11 等效宏观模型
忆阻器
忆阻器是一种新型电子器件,是继电阻、电容、电感后的第四种电子元件。1971年Leon Chua首次预测出忆阻器[1],认为忆阻器可直接将电荷量与磁通量联系起来的基本电路元件。忆阻器具有独特的器件结构和“记忆特性”的电学性能,可高密度集成、低功耗且高速开关等优点,并可与传统的CMOS工艺兼容,被广泛应用于数据存储、逻辑运算、神经网络等领域。根据材料和物理机制,忆阻器件可分为阻变存储器(Resistive Random-Access Memory, 简称RRAM或ReRAM),相变存储器(PCRAM),磁随机存储器(MRAM)和铁电随机存储器(FeRAM)等不同种类。此外还有光电忆阻器、有机材料忆阻器、流体忆阻器等。
最早的忆阻器模型由惠普公司提出,并于2008年在Nature上发表The missing memristor found论文[2]。这里以该忆阻器模型为例来解析典型的忆阻器阻变原理,它可类比于两个可调的滑动变阻器串联,如图12所示。图中的忆阻器是一种无源二端器件,其两端由铂电极构成,中间则是二氧化钛薄膜。这层薄膜分为两层,一层是缺氧二氧化钛(TiO2-x),另一层是无缺氧二氧化钛(TiO2)。其中,缺氧二氧化钛也被称为掺杂氧空位的二氧化钛,对应于Doped区;而无缺氧二氧化钛对应于Undoped区。在Doped区,由于含有氧空位,其导电性较高;而Undoped区则不存在氧空位,因此具有较高的阻抗性。忆阻器的总阻值是由两个区域电阻值的串联相加,由惠普公司发表的论文里提到的忆阻器公式如式4所示。
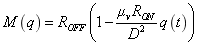
(4)
其中,D为两电极之间夹杂的薄膜厚度;w(图12中)为掺杂氧空位的二氧化钛区域宽度,取值范围为0到D之间;ROFF是w=0,忆阻器介质材料由 Undoped 区组成,阻值达最大;
RON是w=D,忆阻器介质材料由 Doped 区组成,阻值达最小;μv为离子平均漂移速度,受材料以及所加的电压的大小和方向控制;q(t)为电荷量,D越小μv越大时,q(t)的变化更能引起忆阻器阻值的变化。
图12中可知,当加正向电压时,掺杂氧空位会向无缺氧二氧化钛区域移动,w变大,相当于RON和ROFF两个滑动变阻器都向右端滑动相同的距离,则RON的滑动变阻器的阻值增大,而ROFF的滑动变阻器的阻值减小,但由于RON<
因此,HP忆阻器可类比为电荷控制的两个串联的阻值可调的滑动变阻器模型,可直观的看到阻值变化过程,且忆阻器的阻值M变化取决于D和μv,μv值的大小受材料及忆阻器两端所加的电压的大小和方向控制。
图12 忆阻器类比两串联的滑动变阻器模型
用宏原型方法理解RC滤波器
最基础的RC无源滤波器由一个电阻和一个电容构成,分低通和高通两种RC滤波器。总所周知,电容的阻抗与输入信号频率相关,电容的输入信号频率越高,电容的阻抗越小,信号越容易通过,根据该特点设计RC滤波器。RC滤波器所对应宏观世界中的模型可由R的宏观模型和C的宏观模型组合。RC滤波器的截止频率计算公式如式5所示。
(5)
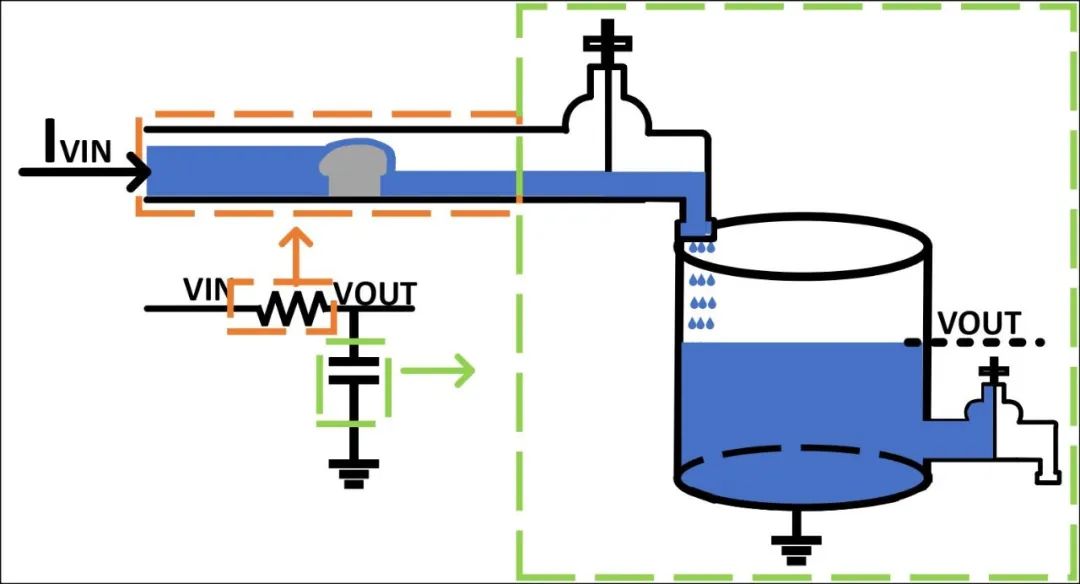
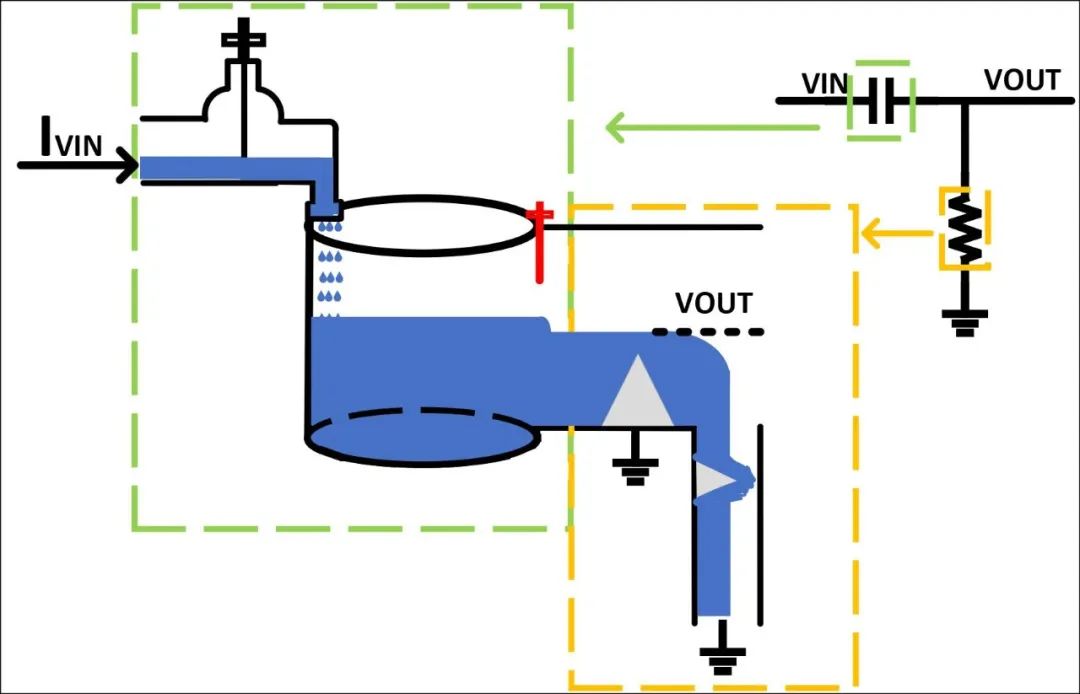
RC滤波器宏观模型如图13所示,图中的蓝色是水流(电流的类比),电阻的输入电压类比为管道左侧水流的高度,电容的输入电压控制圆柱体两个阀门的开和关,电路的输入电流(其大小与输入电压相对应)和输出电压在图中已标注。
图13(a)是RC低通滤波器等效宏观模型,假设一个低频信号输入(频率小于RC滤波器的截止频率),此时,圆柱体的两水龙头的阀门不敏感(电容阻抗大),圆柱体的上下两个水龙头会根据输入信号的正反交替打开,圆柱体内的水面高度(电容上极板的电压值或输出电压值)会随其变化。因此输出信号跟随输入信号变化,无滤波。若输入高频信号(频率大于RC滤波器的截止频率),此时,圆柱体的两水龙头的阀门很敏感(电容阻抗小),圆柱体的上下两个水龙头无法响应输入信号的正负交替打开,而是一直打开,流入圆柱体的水流同时流出圆柱体,圆柱体内的水面高度为零,因此输出电压为零,输入电压被滤除。
图13(b)是RC高通滤波器等效宏观模型,假设一个高频信号输入(频率大于RC滤波器的截止频率),此时,圆柱体的两阀门很敏感(电容阻抗小),圆柱体的两阀门无法响应输入信号的正负交替打开,而是一直打开,流入圆柱体的水流同时流向堵塞的管道(电阻),最后流入地,因此输出信号跟随着输入信号变化而变化,无滤波。若输入低频信号(频率小于RC滤波器的截止频率),此时,圆柱体的两阀门不敏感(电容阻抗大),圆柱体的两阀门会根据输入信号的正反交替打开,值得注意的是中间阀门刚打开时,由于之前圆柱体内积累的水面高,压差大,水流急,当完全打开时,水流已经流入到地,因此,输出电压为零,输入电压被滤除,且频率越低,中间阀门打开越慢,输入电压被滤除的越彻底。
(a)RC低通滤波器等效宏观模型
(b)RC高通滤波器等效宏观模型
图13 RC滤波器宏观模型
审核编辑:汤梓红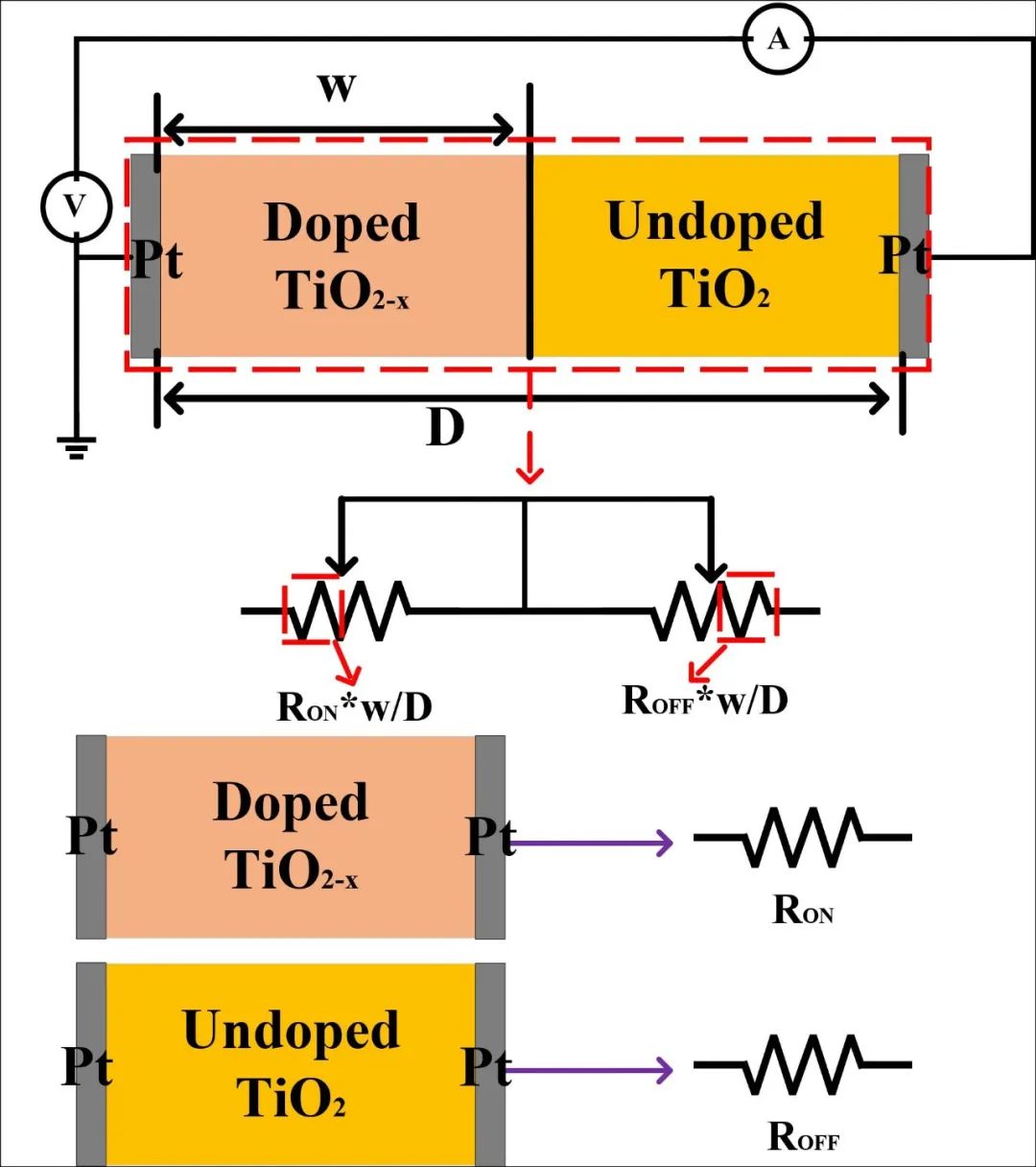
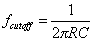
-
新型微电子器件新突破 CPU提速有望2013-08-15 1858
-
微电子器件可靠性失效分析程序2024-11-01 2096
-
电力电子器件课件2009-09-16 13368
-
微电子器件试验方法和程序2012-07-02 2025
-
微电子器件做研究非得去学科前五名的学校吗?2013-09-10 3589
-
集成微电子器件2018-11-07 2406
-
电子器件是指什么?电子器件可分为哪几种2021-11-05 3952
-
新老电子器件的替换问题2023-03-14 962
-
电力电子器件及应用2009-04-14 2469
-
微电子器件应用中的几个重要问题2009-08-27 1091
-
电力电子器件电子教案2009-09-19 546
-
电力电子器件与应用2012-06-19 34370
-
基于微电子器件应用中的几个重要问题2017-10-18 1324
-
光电子器件有哪些_光电子器件介绍2018-02-24 48185
-
电力电子器件分类_电力电子器件的特点2021-01-07 43209
全部0条评论

快来发表一下你的评论吧 !

