计算机原码、反码、补码的概念

在计算机内部数值是以补码的方式进行存储的，采用补码进行数据存储当然有其优点，下面会一一介绍相关内容，让各位彻底弄懂原码、反码、补码的概念以及为什么采用补码作为数据存储的方式。

注意：下面列举的例子均是指8位的字节数据。对于16位，32位的数据同样适用，只是为了书写方便，8位是最好的选择啦！

1、无符号数与有符号数

在介绍原码、反码和补码的概念之前，先来了解下无符号数和有符号数。

在计算机系统中，我们可以将数分为两类：无符号数和有符号数。无符号数的意思是我们不关心这些数的符号，因此也就无所谓正负，反正它们就是数而已，就像小学生一样，眼中只有自然数。在8位的字节运算中，无符号数的范围是0000_0000B~1111_1111B，即十进制的0~255。

有符号数是分正负的，而且规定，数的正负要通过它的最高位来辨别。如果最高位是0，它就是正数；如果是1，就是负数。这样一来，在8位的字节运算环境中，正数的范围是0000_0000B~0111_1111B，即十进制的0~127；负数的范围是1000_0000B~1111_1111B，即10进制的-128~-1。也就是说8位的数据，有符号数的范围是-128~127（对这里的负数有疑问的可以往下面看）。

2、原码、反码与补码

原码：最高位表示符号位，其余位代表数值大小。如果最高位是0，它就是正数；如果最高位是1，就是负数。例如：十进制数+2，其二进制形式为：0000_0010B；如果是-2，就是1000_0010B。因为最高位是符号位，所以原码二进制的形式值不等于真正的数值。例如上面的有符号数1000_0010B，其最高位1代表负数，表示的数值为-2，而不是形式值130（1000_0010B转换成无符号十进制等于130）。

反码：正数的反码是其本身；负数的反码是在原码的基础上，符号位不变，其余各数值位取反。

补码：正数的补码是其本身；负数的补码是在其原码的基础上，符号位不变，其余各数值位取反，最后+1（即负数的补码是其反码+1）。

下面列举几个8位二进制数的原码、反码和补码的编码形式：

十进制数	原码	反码	补码
42	0010 1010	0010 1010	0010 1010
-42	1010 1010	1101 0101	1101 0110
127	0111 1111	0111 1111	0111 1111
-127	1111 1111	1000 0000	1000 0001

3、补码存储数据的优点

在讲述原码、反码和补码时，有一个特殊的数值没有涉及到，那就是0，在我们平时使用中，0是没有正负之分的，但是不可否认+0 = -0，那么下面列举下+0，-0的原码、反码与补码的形式：

十进制数	原码	反码	补码
+0	0000 0000	0000 0000	0000 0000
-0	1000 0000	1111 1111	0000 0000

为什么-0的反码1111_1111B进行加1操作求取到的-0补码是0000_0000B。因为这里假定数据宽度是8位的，1111_1111B加1之后，会逐个向上进位，我们假定有第9位，且值为0，那么0_1111_1111B加1之后，就变成了1_0000_0000B，但是实际上我们要的数据是8位的宽度，这里舍弃第9位，最后结果就变成了0000_0000B。

好了，在讲述补码的优点之前，先看看计算机为什么不使用原码作为数的存储格式而采用补码作为数的存储格式。

下面说说原码的优缺点吧。

原码的优点当然是简单直观，例如+2的原码为：0000_0010B，-2的原码为：1000_0010B。

原码的缺点也显而易见：

(1)、+0与-0在原码中竟然有两个二进制形式，与我们熟知的+0=-0貌似有出入。

(2)、原码不能直接参加运算，可能会出错。例如：1+(-1)=0，而用原码的二进制形式进行运算为：0000_0001B + 1000_0001B = 1000_0010B，换算成十进制为-2，显然计算结果错误。

那么计算机为什么要使用补码呢？

首先，根据运算法则减去一个正数等于加上一个负数，即: 1-1 = 1+(-1)，所以计算机被设计成只有加法而没有减法，而让计算机辨别”符号位”会让计算机的基础电路设计变得十分复杂，于是就让符号位也参与运算，从而产生了反码。

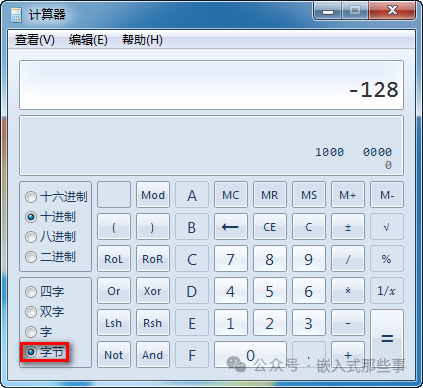
用反码计算，出现了”0”这个特殊的数值，0带符号是没有任何意义的。而且会有0000_0000B和1000_0000B两个原码编码表示0。于是设计了补码，负数的补码就是反码+1，正数的补码就是正数本身，从而解决了0的符号以及两个编码的问题：用0000_0000B表示0，用1000_0000B表示-128。

注意：-128并没有原码和反码。使用补码，不仅仅修复了0的符号以及存在两个编码的问题，而且还能够多表示一个最低数值。

如果还不清楚-128怎么来的，那么我就来按我的想法来推出来吧，-127的原码为：1111_1111B，则其反码为：1000_0000B，补码为：1000_0001B，那么自然我们可以想想补码为1000_0000B代表的就是-128=-127-1=1000_0001B - 1= 1000_0000B。这也就是8位数据最小的负整数了。

这就是为什么8位二进制，使用补码表示的范围为[-128,127]。

补码存储数据的优点：

(1)、避免了0的编码有两个；

(2)、符号位和有效值位可以一起处理，减法通过加法就可以实现，即简化了计算机的结构设计也提高了运算速度。

补码存储数据的缺点：

(1)、不够简单直观。当然这里的不够简单直观是对我们来说的。计算机倒没什么。

下面给大家推荐一个计算补码的小工具，那就是我们经常使用的Windows计算器，只要选择好相应的数据宽度，输入你的数值，就可以观察到对应的二进制形式了：

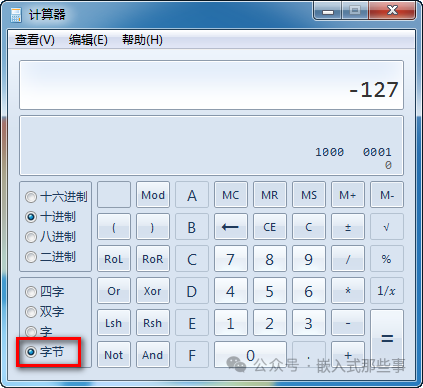
2018-12-25_191046

好了，讲了这么多，相信大家对原码、反码和补码都有一定的认识了。

　　审核编辑：汤梓红