

粘接层空洞对功率芯片热阻的影响
描述
共读好书
潘浩东 卢桃 陈晓东 何骁 邹雅冰
(工业和信息化部电子第五研究所)
摘要:
采用有限元数值模拟方法,建立金氧半场效晶体管(MOSFET)三维有限元模型,定义不同大小和位置的粘接层空洞模型,对器件通电状态下的温度场进行计算,讨论空洞对于热阻的影响。有限元仿真结果表明,随着芯片粘接层空洞越大,器件热阻随之增大,在低空洞率下,热阻增加缓慢,高空洞率下,热阻增加更明显;总空洞率一致时,不同位置空洞对应器件热阻的关系为中心空洞>拐角空洞>阵列空洞。采用双界面法对含有空洞缺陷的器件进行了热阻测试,将试验数据修正仿真结果,获得准确的空洞-热阻曲线,对于芯片粘接空洞工艺控制提供理论参考。
0 引言
在电子行业,功率器件应用广泛,国内外学者对于功率器件的可靠性做了大量的研究,其中对于功率器件的散热性能尤为关注。研究表明,温度的上升会大大提高芯片失效的概率,温升每达到10 ℃,失效概率能提升一倍 [1] 。对功率器件的散热影响最为关键的结构是芯片粘接界面,粘接界面空洞的存在会提高器件的热阻,降低器件的散热性能。
谢鑫鹏等利用有限元法研究了功率芯片粘接层空洞对器件温度场和应力场的影响,分析了芯片粘贴工艺中空洞成型的机理。Katsis D C等对功率循环后的芯片热阻进行了研究,在经历了7 000个循环后,芯片热阻增加了一半,在多次循环后芯片粘接层的空洞达到了50% [2] ;Fleischer A S等对粘接层空洞与器件热阻的关系进行研究,发现热阻随空洞体积增大而增大 [3] ;章蕾等人采用有限元方法进行了空洞对器件封装温度影响的研究,为提高封装的可靠性提供了理论依据 [4-5] 。采取有限元数值模拟仿真的方法对芯片粘接层空洞进行相关研究,优点是建立模型简单,相较于制备试验样品,能节省大量人力机时,但是由于数值模拟难以模拟所有试验环境,因此所得到的结果往往有所失真,需要通过部分真实的试验数据来校核修正。
本文将采用有限元数值模拟仿真的方法对芯片粘接空洞,研究不同位置和不同大小的空洞对于器件温度场影响,并计算器件结壳热阻;同时对涵盖不同空洞缺陷的试验样品进行热阻测试,并以试验数据修正仿真结果,建立准确的热阻-空洞率曲线,为实际工艺提供理论指导。
1 热分析理论及测试原理
1.1 热分析理论
有限元热分析是将所研究对象划分成有限个单元,通过热平衡和能量守恒定律,计算各单元节点的温度或者其他热相关的物理参数。针对机械电子领域的很多复杂的热-力学工程问题,采用有限元热分析法是一种有效的求解方法。在热分析中,常涉及的传热方式一般有三种,分别是热传导、热对流和热辐射。针对不同的传热方式,设置不同的分析参数进行求解计算 [6] 。
在进行热分析仿真计算时,可选择采取稳态分析或者瞬态分析两种方式,当所研究系统各点的温度仅随位置的变化而变化,不随时间变化而变化,即可采取稳态分析;而当系统的温度变化除了与位置有关,还与时间相关,此时应采用瞬态分析。稳态热分析的能量平衡方程以矩阵方式表示为 [7] :
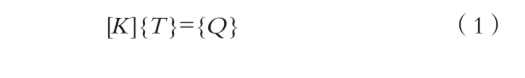
式中:[ K ]代表的是传导矩阵,其中包括热系数、对流系数及辐射和形状系数等物理量;{ T }表示的是节点温度向量;{ Q }是节点热流率向量,热生成也包含在内。
瞬态热分析公式 [8] 表示为:
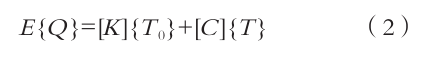
式中:{ Q }表示的是节点热流率向量,包括热生成;[ K ]代表的是传导矩阵,其中包括包含热系数、对流系数及辐射和形状系数等物理量;[ C ]表示的是比热矩阵,包括系统内能的增加情况;{ T }为节点温度向量;{ T 0 }为温度对时间的导数。
瞬态分析相较于稳态分析能够得到随时间变化的一些物理参数,在一些热-力学问题求解过程中往往需用瞬态热分析求解温度场,再将之作为热载荷进行应力分析,瞬态热分析需要定义热传导系数、比热容和密度。对于一些热学问题,若仅仅关注达到热平衡状态时的温度场分布,而不关注中间时刻的温度变化,则选用稳态热分析计算更加简单高效,稳态热分析只需要输入材料的热传导系数。
1.2 热阻测试
根据 JESD51-1规定,半导体器件结到某参考点的热阻值 [9] :
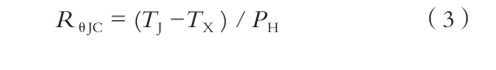
式中: T J 是半导体结温; T X 是参考点温度; P H是半导体的热功耗。根据实际需要选择的不同的参考点,可以定义不同的热阻。功率器件规格书上最常见的热阻参数是结壳热阻 R θJC 和结到环境的热阻R θJA 。所谓 R θJC 就是从半导体芯片的工作部位到距离芯片最近处的封装体外表面(壳)的热阻,类似的R θJA 是芯片工作部位到器件周围的自然对流(静止空气)环境的热阻。
关于热阻测试的方法有很多,本文对于一些具有空洞缺陷的器件进行热阻测试,如图1所示,测试方法参考JESD51-14标准,使用双界面法,使用D-S间寄生二极管压降作为热敏参数。双界面法分两次测试:第一次测试是直接将器件接触到热沉上,第二次测试在器件和热沉之间放置一层导热硅脂。由于两次测试中器件的散热路径的改变仅仅发生在封装壳体之外,因此两条热阻抗曲线的重合部分对应的热阻抗为热量在器件内部热阻抗,即结壳热阻。
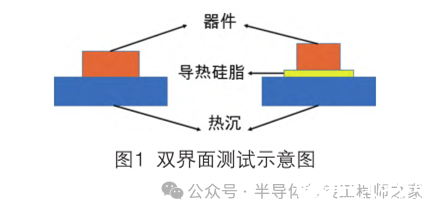
2 试验过程
2.1 仿真模型建立与计算
本文研究以某MOSFET器件为研究对象,对其通电状态下的温度场进行计算,再通过器件结壳温差计算热阻。为了获得收敛和定性结果,对仿真模型进行适当简化,同时假定各材料间的界面为完全连接的理想状态。
器件几何模型如图2所示,结构包括芯片、粘接层、塑封料、金属壳和金属管脚,对粘接层不同空洞率和不同空洞位置定义如图3所示,空洞位置包括中心、边角和阵列分布,所有空洞均定义为贯穿型空洞。
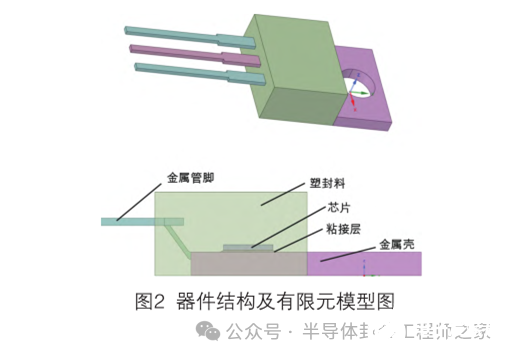
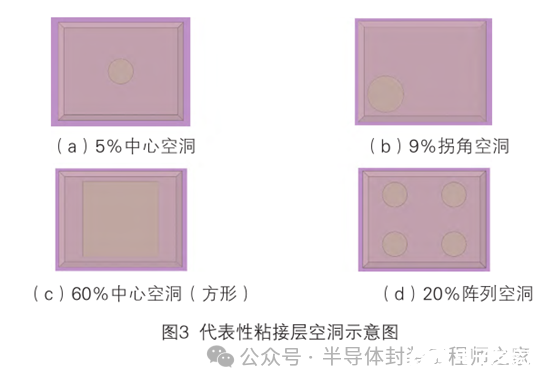
在定义材料属性的时候,赋予模型各结构材料的热传导系数,具体材料属性见表1。
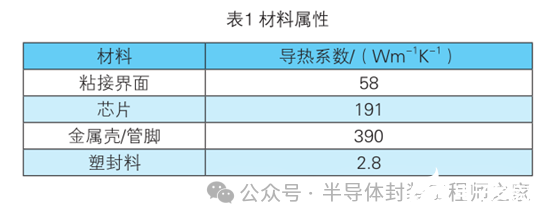
模型划分网格采用扫掠方式为主、多区域为辅的划分方式,生成六面体单元,在网格划分的时候考虑计算收敛性和结果的准确性,对芯片和粘接界面的网格进行细化,器件网格划分结果如图4所示。

在进行有限元分析时,对几何模型做出假设:
1)认为芯片为主要的发热器件,忽略通电时其他结构产生的热量;
2)除去预先设定的空洞缺陷之外,认为烧结界面层其他部位结构均匀,没有间隙,无其他缺陷存在;
3)认为器件产生的热量完全由与其接触的粘接层和塑封料导出;
4)认为主要热交换方式为热传导和热对流,忽略热辐射的影响。
针对应用工况,设置边界条件为:对芯片施加10 W的功率,环境温度设定为25 ℃,器件与空气对流换热系数为5 W/(m 2 ·℃),器件下端与散热台相接触,给定一个换热系数3 000 W/(m 2 ·℃)作为边界条件,采用稳态热分析方式。
2.2 试验样品制备与测试条件
经过工艺调整之后制备特定位置、一定比例空洞的缺陷样品,由于缺陷样品制备具有一定随机性,仅以单一中心空洞(忽略大面积空洞周围的小空洞)缺陷品为试验样品进行热阻测试,并与仿真结果进行对比,代表性图片空洞分布情况如图5所示。

对含有特定缺陷的MOSFET器件进行热阻测试,通过改变电子器件的输入功率,使得器件产生温度变化,在变化过程中,测试出芯片的瞬态温度响应曲线。具体测试参数为:测试电流50 mA,加热电流10 A,加热时间30 s,降温时间60 s。
3 结果与讨论
对不同空洞缺陷的模型分别进行热仿真计算,图6为中心5%空洞模型计算结果温度云图,从图中可见器件整体及芯片的的温度分布,在设定的环境温度和功率下,器件芯片作为热源,只能通过与塑封料和粘接层的热传导才能与外界进行热交换,该部位温度最高。

从芯片温度云图上能看出,温度分布和粘接层缺陷特征相互对应,器件的最高温度位于芯片中心处,形成了中央温度高且向四周方向逐渐递减的温度分布趋势,器件温度最低的区域为与散热台接触的金属面,与散热台的快速热交换使其温度快速下降,在热稳定状态下,其温度接近于室温,但由于器件壳体表面温度相差太大,任意取一个节点的温度无法完全代表壳体温度,因此以有限元计算所得的壳体单元平均温度为壳温,通过给定功率和结壳温差计算结壳热阻,对比粘接层不同空洞缺陷对应器件结壳热阻的差异。
图7为不同空洞缺陷烧结界面对应的和芯片温度分布云图,从云图温度分布形态一定程度上反映了空洞的缺陷类型,相较于粘接层,空洞的导热率很低,随着空洞面积增大,温度传导热阻越大,芯片散热性能越差,对应的芯片结温越高。
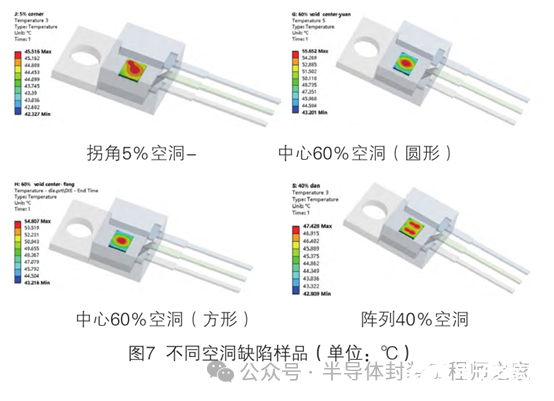
不同空洞率的烧结界面缺陷计算的芯片温度和壳体温度数据及计算得出的热阻值见表2。
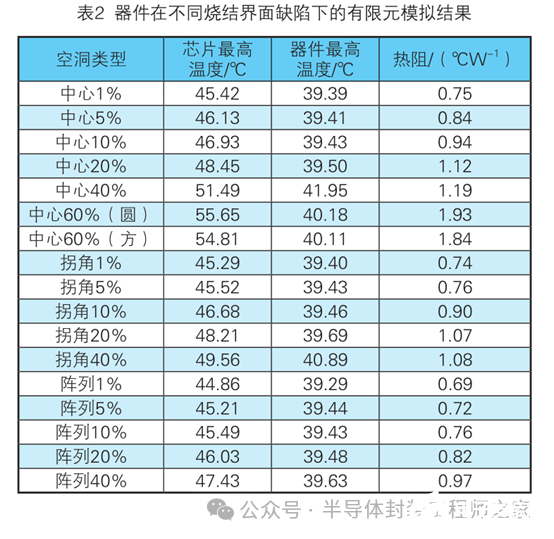
对比相同空洞率但空洞位置不同器件的热阻大小,发现当空洞处于拐角处时,器件热阻更小。
由于芯片的发热由中心四周散开,当空洞位于中心时,芯片中心热量有两种传递方式:一种是沿空洞垂直传导,一种是先水平传导至无空洞区,再沿着粘接界面垂直传导于器件底部。由于空洞热导率小,显然第一种传导方式热阻大;而当空洞位于拐角处时,芯片中心热量则可直接沿着中心垂直传导,而拐角处热量较少,沿着空洞传导。综上所述空洞在中心处时热量传导效率比空洞在拐角处要低,器件热阻较大。
分析不同阵列空洞仿真结果可知,随着阵列空洞占比增大,器件热阻增大,规律与单一空洞一致,空洞范围越大,热量传导越困难。与单一空洞相比,阵列空洞将大空洞分成了四个对称的小空洞,通过表2中数据对比可知,总空洞率一致时,大空洞器件热阻要比多个小空洞器件热阻大,在各个小空洞之间存在完整的粘接层,热量可通过空洞之间的粘接层垂直传热,热量传导效率更高。
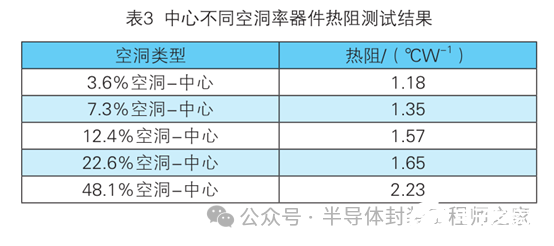
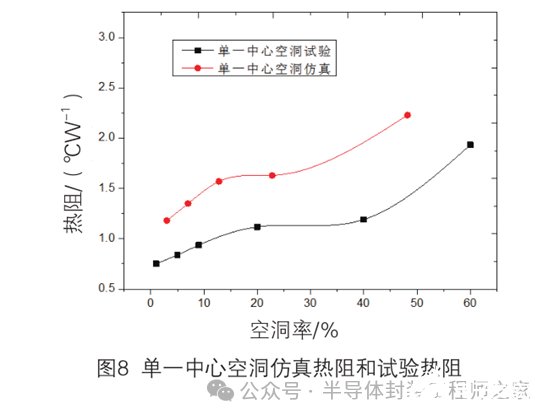
针对具有中心单一空洞的缺陷器件,热阻测试结果见表3,将中心空洞对应仿真计算结果与试验数据进行对比,拟合如图8所示,从图中可以看出仿真与试验趋势基本吻合,但由于仿真处于完全理想化的状态,试验又无法避免一定的环境与设备误差,二者在量值上存在一定的差异。
依据试验数据,将仿真数据曲线逼近于试验数据曲线,修正仿真曲线,修正后曲线如图9所示。从图中中心单一空洞曲线图可知,仿真与试验趋势基本吻合;对于其他空洞分布类型,由于缺陷试验样品的梯度不充分,仅展示仿真结果,通过中心单一空洞这一分布类型进行类比修正仿真曲线。
伴随着空洞率的增大,器件热阻整体呈现随之增大的趋势,空洞率在20%以下和40%以上时,热阻增大趋势很明显,空洞率在20%~40%之间时,热阻增大的趋势则不明显。当空洞率在20%以内时,器件的热阻随着空洞率增大而增大,当空洞率在20%~40%之间时,器件热阻随空洞率增大而减少;当空洞率在40%以上,器件热阻随空洞率增大而增大,当烧结界面空洞率达到一定值时,器件的热阻将会有一个非常急剧的升高,严重影响芯片的散热性能。
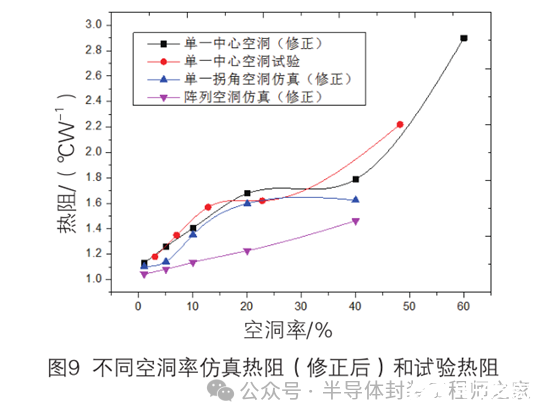
对于单一中心空洞,修正后的仿真和试验曲线吻合度较高,同时可以直观地看出中心空洞、拐角空洞、阵列空洞对于热阻影响的不同。对于相同空洞率,器件热阻呈现的规律为中心空洞>拐角空洞>阵列空洞。一般来说,器件本身对于热阻的上限是有规定的,通过修正后的曲线能够将粘接面空洞和器件热阻建立较准确的关系,对于控制器件的热阻具有很好的指导意义。
4 结论
本研究对缺陷MOSFET器件进行了热分析模拟和热阻测试,得出器件结温和壳温,并结合功率计算MOSFET器件的热阻值,主要研究结果为:
1)芯片粘接界面的空洞占比越大,器件的结壳温差越大,器件的热阻值越大。
2)相同空洞率时,空洞位置在中心相较于在拐角处,器件热阻更大,单一空洞相较于阵列空洞器件热阻更大。
3)通过热阻实测数据修正仿真曲线,二者吻合度较高,根据修正后的曲线可以预测不同位置空洞和空洞率不合格的器件热阻,并提供一定工艺指导。
审核编辑 黄宇
-
检查焊点中的空洞2018-03-20 6169
-
如何选择合适的芯片粘接方法?从基础到应用的全面指南2023-09-02 3210
-
芯片粘接失效模式和芯片粘接强度提高途径2023-10-18 2563
-
技术分享 | 芯片粘接空洞的超声检测2024-04-11 3527
-
芯片用什么胶粘接牢固?2024-08-15 2681
-
功率器件的热设计基础(二)——热阻的串联和并联2024-10-29 1417
-
湿度大揭秘!如何影响功率半导体器件芯片焊料热阻?2025-02-07 1502
-
精通芯片粘接工艺:提升半导体封装可靠性2025-02-17 2144
全部0条评论

快来发表一下你的评论吧 !

