

卡尔曼滤波家族
描述
最近在看 《概率机器人》,觉得关于贝叶斯滤波器确实也可以稍作总结,于是就写了这篇卡尔曼滤波家族。
本文对于扩展卡尔曼滤波、无迹卡尔曼滤波仅仅做了一些简要介绍,不再想上次的文章那样做详细地推导了。但只要看过之前写的卡尔曼滤波,相信这篇文章对于你来说也是很好理解的。
本文配图均来自《概率机器人》
扩展卡尔曼滤波
假设状态转移概率和测量概率分别由非线性函数g和h控制,而不再是一个线性变换:
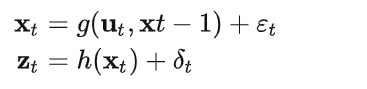
这种情况下,由于线性变换的关系不在了,因此概率分布也不再是高斯分布。整个系统不再有闭式解,这是最让人头疼的。
而EKF的主要思想就是线性化:通过一个在高斯函数的均值处与非线性函数g相切的线性函数来近似g。
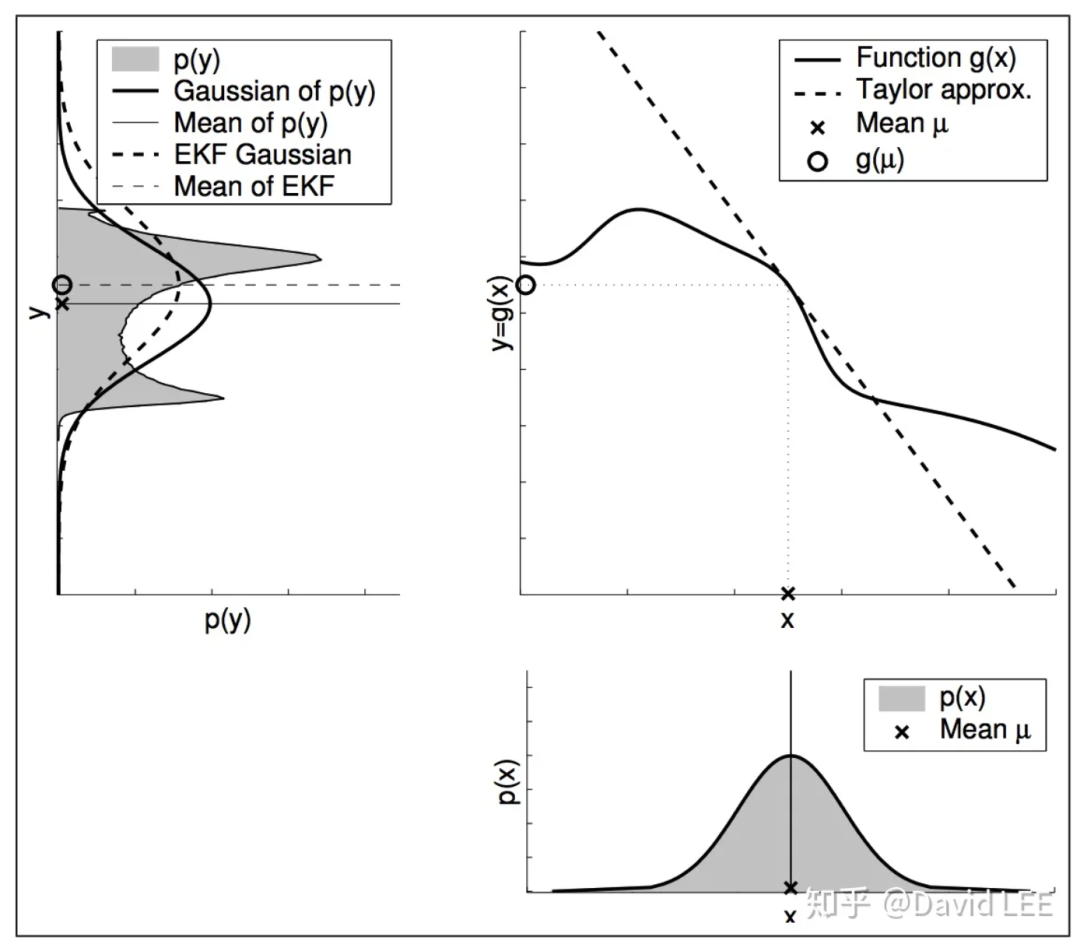
线性化的主要优点就是效率,一旦对g和h进行了线性化,KEF和KF就是等效的。
EKF采用一阶泰勒展开的方式来进行线性化,其根据g的值和斜率构造一个函数g的线性近似函数:
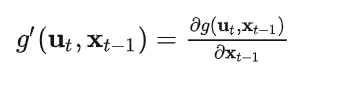

同理,将测量函数h线性化,有
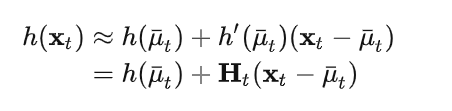
最后,整个EKF算法的流程如下:
1. 运动更新:
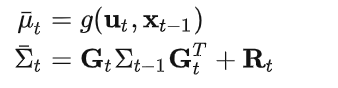
2. 测量更新
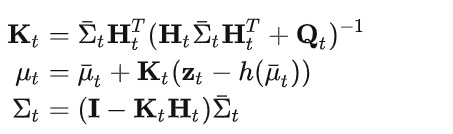
很显然,EKF 能否成功应用取决于两个因素:
1. 被近似的函数的局部非线性化程度;
2. 概率分布自身的不确定度(协方差)。
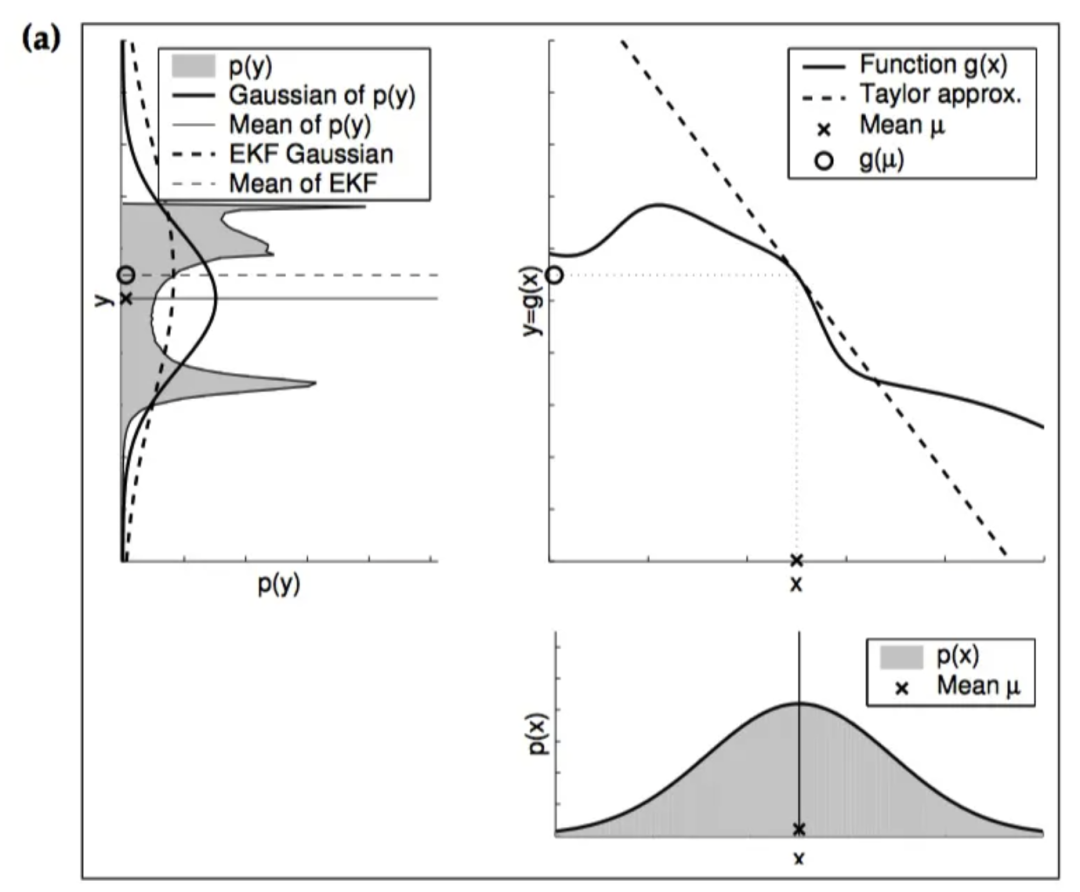
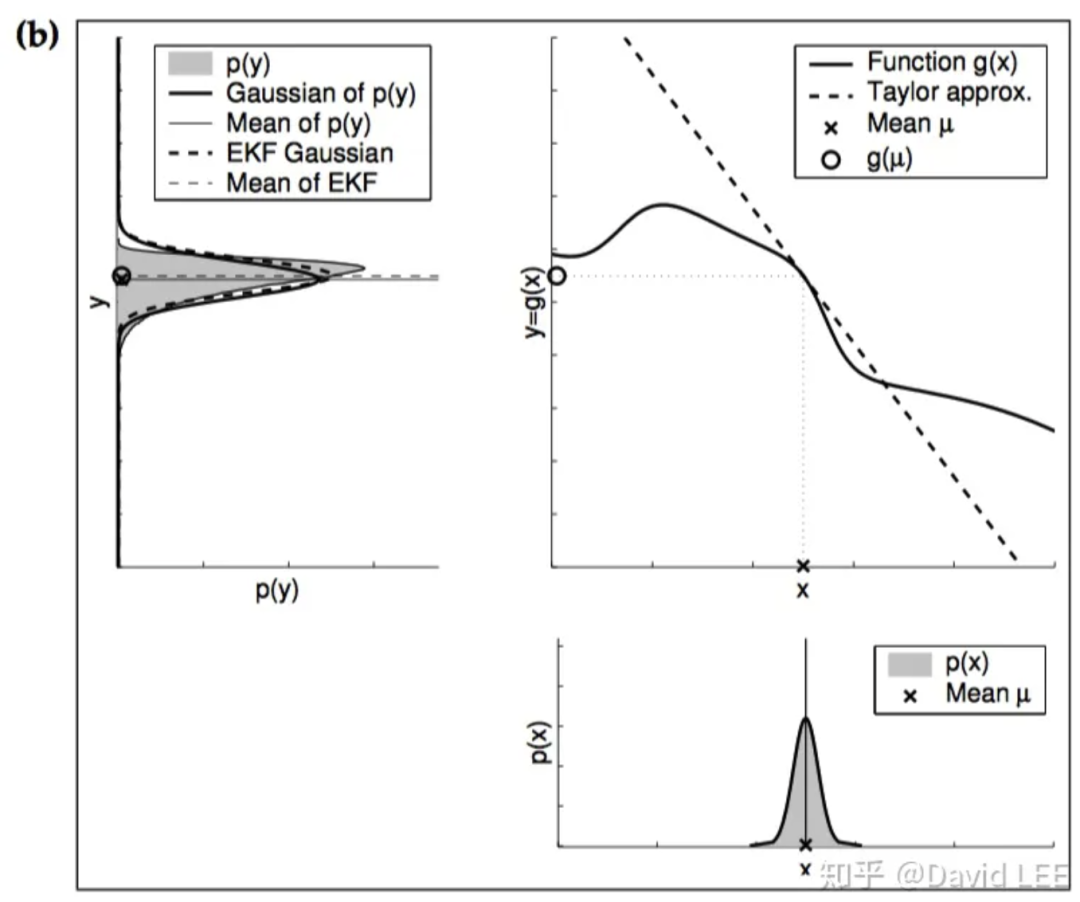
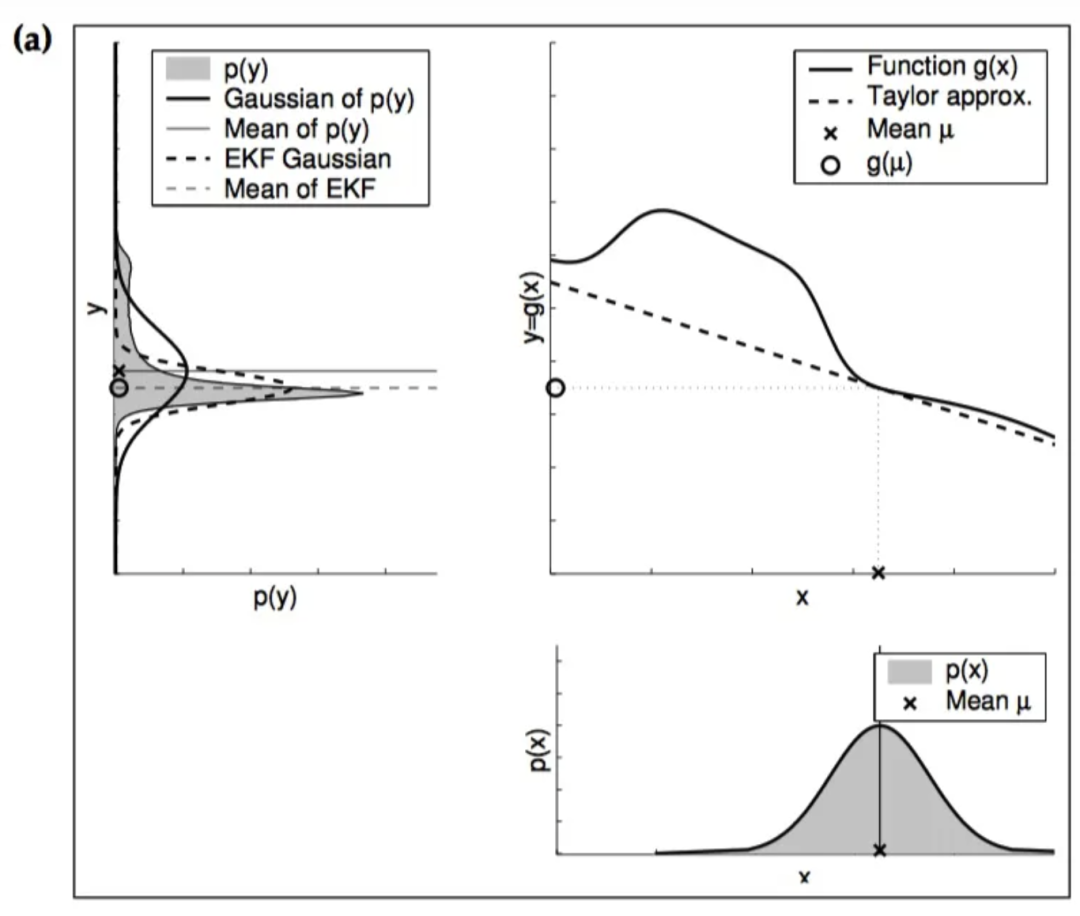
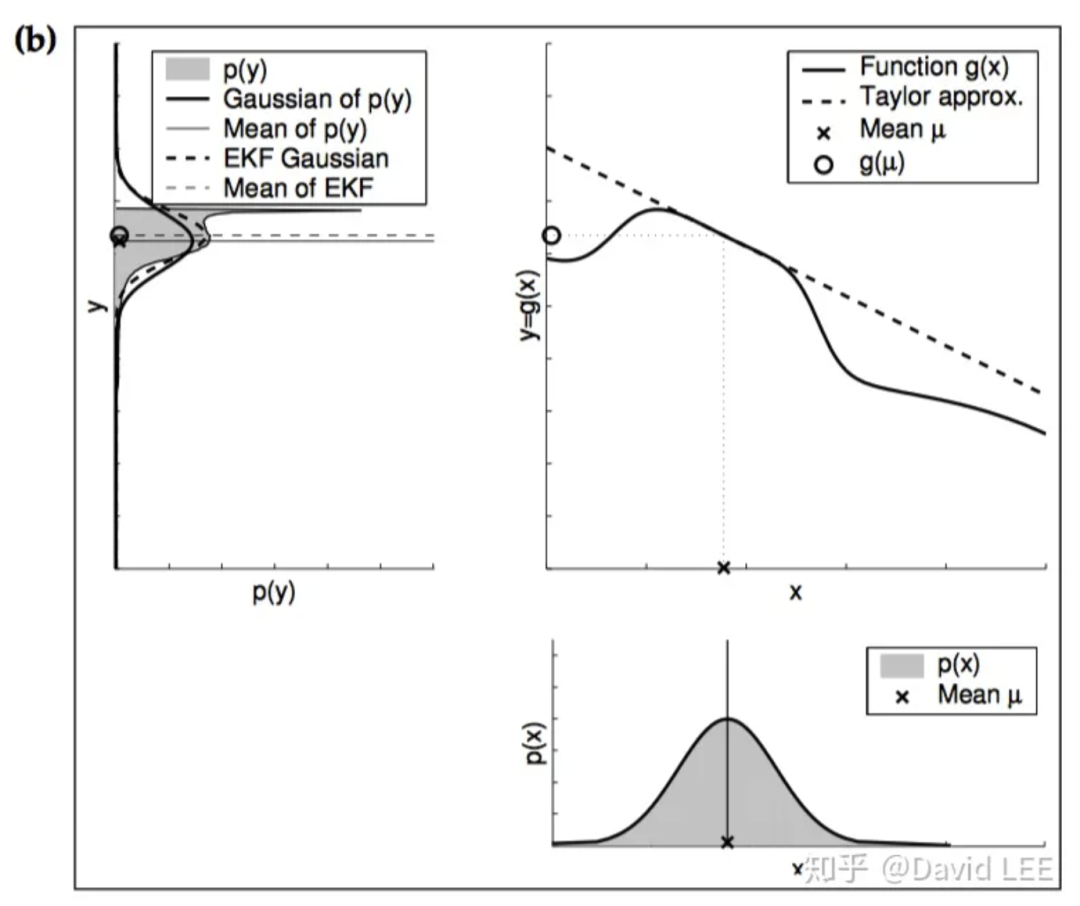
上两图就明确展示了非线性函数在近似点非线性程度越高、概率分布本身越不确定,所得到的近似结果就越差。此时,采用扩展卡尔曼滤波的效果往往很差,甚至会导致发散。
无迹卡尔曼滤波
不同于EKF使用线性化来近似非线性函数,UKF通过无损变换来近似一个高斯分布,它通过使用加权统计线性回归过程来实现随机线性化。
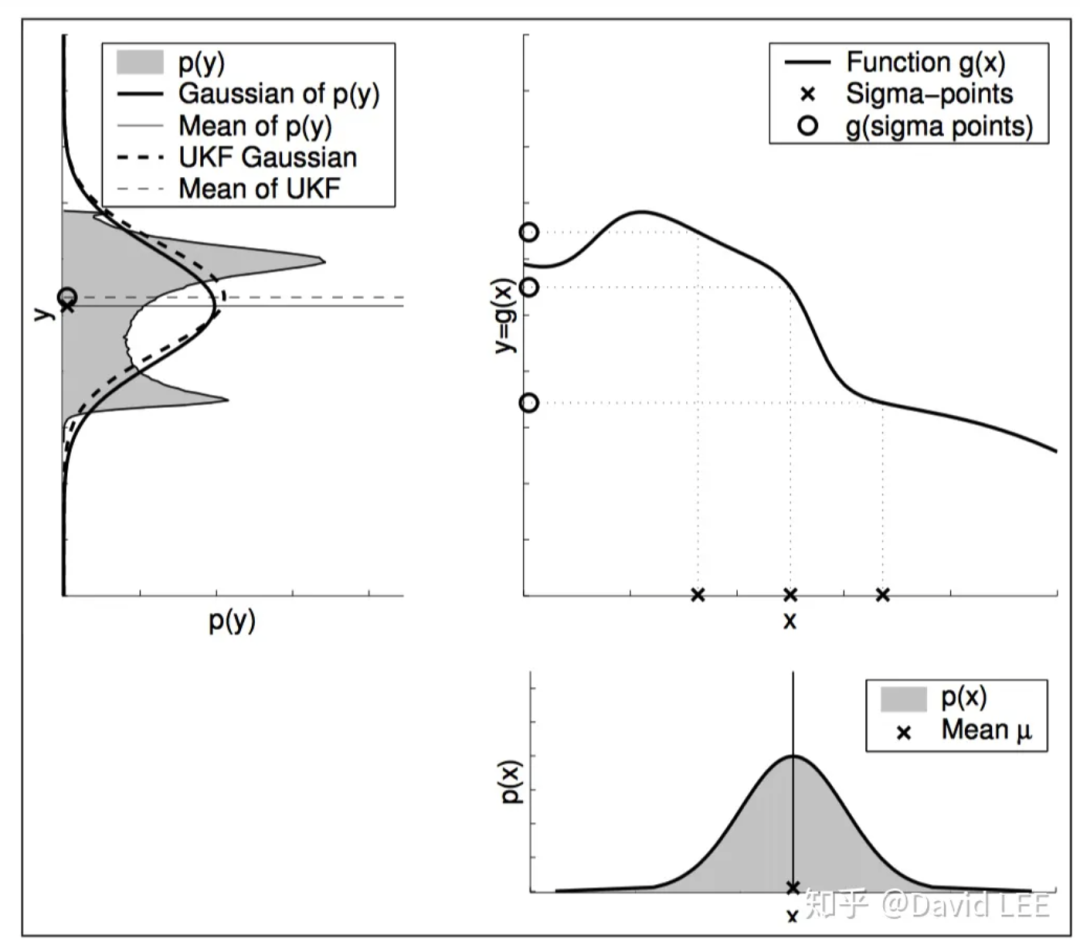
下面就介绍些UKF无损变换的思想。


将以上过程分别代入到运动更新和测量更新中就可以得到无迹卡尔曼滤波了。
运动更新

测量更新


以上就是扩展卡尔曼滤波和无迹卡尔曼滤波的全过程了。只要明白了贝叶斯滤波或者卡尔曼滤波器,这两个扩展都是信手拈来。
SLAM中,KEF往往比UKF使用得更广。我个人浅见,主要原因有一下几点:
1. UKF是一种抽样近似,无可避免地导致计算量较大;
2. 只有在高度不线性的情况下(或方差很大),UKF才有明显的优势;
3. UKF的优势主要集中在开环的情况下,但SLAM中更常使用回环检测这样的闭环来消除误差;
4. 如果建图与定位分开,UKF在建图过程中的作用可能会大些(开环的情况下);在定位中,用其来提高运动模型作用不大,观测模型中准确地和地图进行匹配对定位精度影响更大。
信息滤波
信息滤波(IF)是卡尔曼滤波的对偶滤波算法,二者的不同在于对高斯分布的表示方式。
信息滤波以正则参数来表示高斯分布,由一个信息矩阵和信息向量组成。

该式在一些情况下会比矩参数(卡尔曼滤波中均值和协方差分别是一阶矩和二阶矩)的表示更加简洁。例如,信息滤波下高斯分布的负对数为
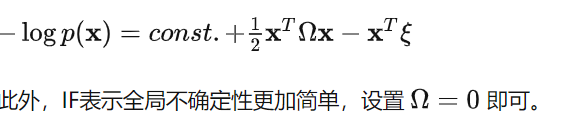
对应的信息滤波算法和扩展信息滤波算法如下。
信息滤波算法
对应的运动方程和测量方程为
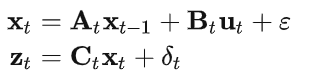
对应的信息滤波算法为:
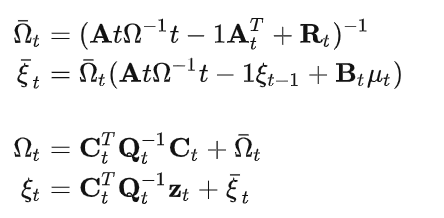
对比信息滤波算法和卡尔曼滤波,二者在计算复杂度上有很大的不同。
信息滤波中运动更新涉及矩阵求逆,计算量大;但在卡尔曼滤波中运动更新只涉及状态向量的一部分。
而信息滤波中测量更新是增量的,而KF的测量更新涉及矩阵求逆而较为困难。这也展示了二者的特性是对偶的。
扩展信息滤波算法
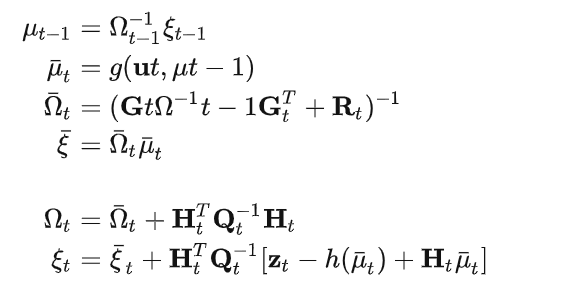
-
卡尔曼滤波2013-07-04 3061
-
卡尔曼滤波有哪些应用2021-07-12 1940
-
卡尔曼滤波简介2022-02-28 2138
-
卡尔曼滤波器原理2008-07-14 1296
-
卡尔曼滤波器原理简介2015-12-15 1044
-
卡尔曼滤波学习及应用2016-04-13 966
-
卡尔曼滤波算法2016-12-17 1135
-
一文看懂mpu6050卡尔曼滤波程序2018-03-09 76208
-
几种最优估计和卡尔曼滤波原理的学习课件免费下载2020-05-09 1031
-
卡尔曼滤波原理及应用2022-06-09 581
-
扩展卡尔曼滤波的原理2022-08-12 7081
-
卡尔曼滤波(KF)与扩展卡尔曼(EKF)2023-05-10 842
-
浅析卡尔曼滤波2023-06-14 2916
-
什么是卡尔曼滤波?卡尔曼滤波的作用是什么2023-08-08 8927
-
卡尔曼滤波在图像处理中的应用实例 如何调优卡尔曼滤波参数2024-12-16 2644
全部0条评论

快来发表一下你的评论吧 !

