一次测量以表征对称叠加光学涡旋复振幅单分量

导读

复振幅测量是光场表征的必要前提，在这项工作中，课题组提出了一种仅用CCD记录的一幅图像来表征对称叠加光学涡旋（SSOV）复振幅的一次测量方法。

一次测量方法基于UPOLabs HDSLM80R液晶空间光调制器搭建实验装置，实验结果如图所示，在实验中，该课题组选择了四个典型的SSOV（一阶、低阶、高阶和径向节点）来表征复振幅。

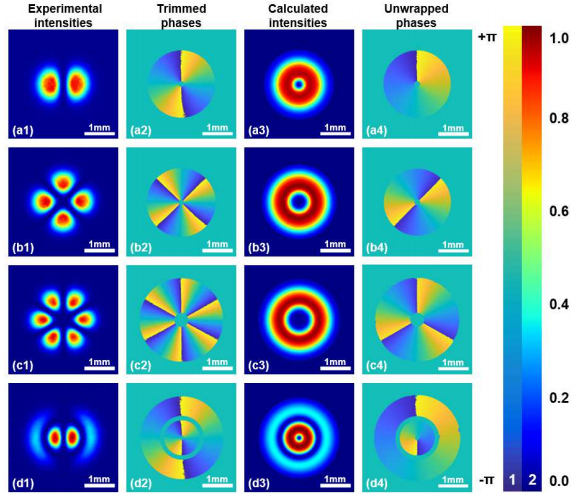
一次性测量的实验结果。（A1-D1）SSOV的干扰强度

主要内容

OV在光学微操作、等离子体激元、旋转探测、光学通信、引力波探测等领域有广泛的应用。这里经常使用对称叠加OV（SSOV）来代替单个组件。在实际应用之前需要表征SSOV中单个分量的复振幅，并测量其模式纯度。它是OV的重要质量参考，决定了OV在各种应用中的性能。

测量叠加OV中单组分模式纯度的实验装置

许多已证明的方法表征和测量SSOV的模式纯度，但最通用的方法是将场分解为模式的相干和，每个模式都有特定的振幅加权和相位：即所谓的模式分解。然而，它需要使用SLM逐个扫描多个全息图来完成测量，测量效率较低。本论文课题组提出的一种仅用CCD记录的一幅图像来表征对称叠加光学涡旋（SSOV）复振幅的一次测量方法，解决了测量效率低等问题，该方法是首次报道的。该方法耗时短，可以在0.24秒内表征SSOV的复振幅，并实现模式纯度的测量。由于使用要测量的SSOV的一部分作为参考光，尽管使用了相移技术，但不再需要额外的参考光束进行干涉，这在以前没有报道过。

一次测量方法包括两种策略。一种是用于振幅测量的环形提取策略，另一种是针对相位测量的旋转测量策略。在概念验证实验中，对复振幅进行了表征，并很好地测量了模式纯度，这种方法具有极好的灵活性，快速性和鲁棒性，可应用于各种场合和恶劣条件。

论文简要介绍了对全息图进行编码以生成SSOV的过程，我们对全息图进行编码，全息图可以用于在纯相位SLM上实现入射光的复数幅度调制。全息图的编码过程如图所示：

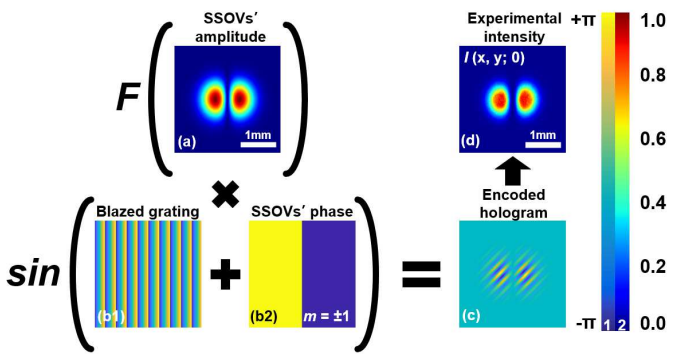
全息图编码示意图

为了通过一次测量获得SSOV的复振幅，课题组提出了两种策略。一种是用于振幅测量的环形提取策略，另一种是针对相位测量的旋转测量策略。环提取策略的示意图如图（a1-a4）所示，旋转测量策略的示意图如图（b1-b4）所示。

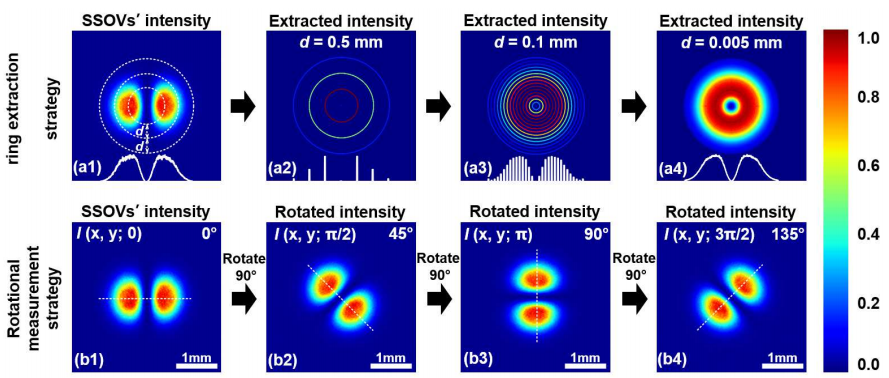
（a1-a4）环形提取策略和（b1-b4）旋转测量策略示意图

从理论上讲，在得到四个强度分布结果后，可以反推导出所需的相位。然而，由于三角函数的引入，在实际计算中，所需的相位被包装成 2π。我们不能通过简单地除以2来获得所需的结果，因此，需要相位展开技术。

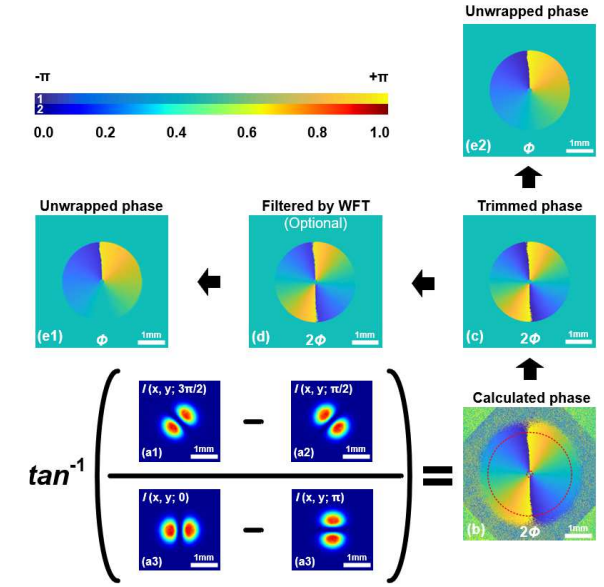
计算所需相位的示意图

为论证误差对测量的影响，课题组从角度误差、径向误差、实验误差三个方面进行了实验论证。

角度误差实验结果如图所示，结果表明它对模型纯度的测量结果几乎没有影响，这充分证明了该方法的稳健性。实验结果表明了旋转测量策略的准确性和鲁棒性。

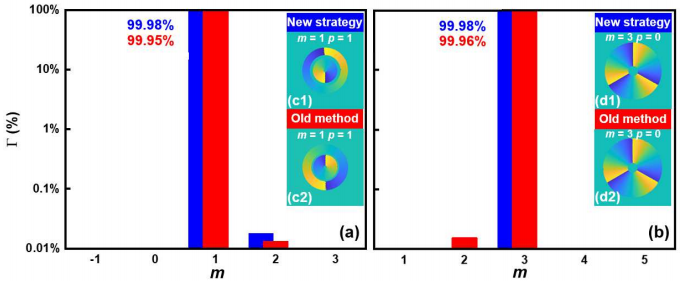
旋转测量策略（新策略）与相移法（旧方法）在OAM光谱测量中的比较。

径向误差实验结果如图所示，结果表明它对模型纯度的测量结果几乎没有影响，这充分证明了该方法的稳健性。

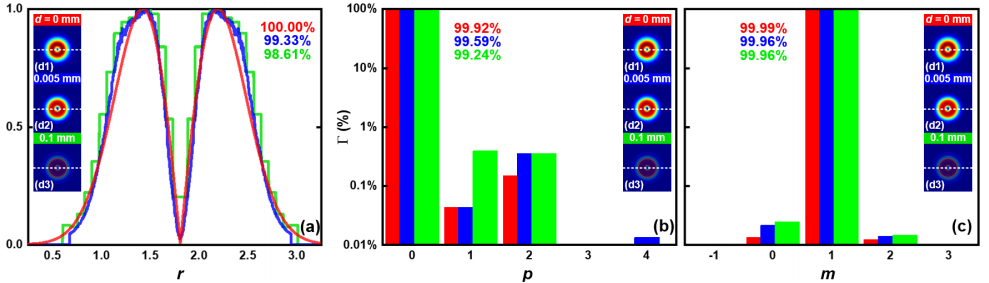
区间d在环形提取策略中引入的径向误差

实验误差结果如图所示，结果表明随着曝光时间的增加，测量的模式纯度略有下降。

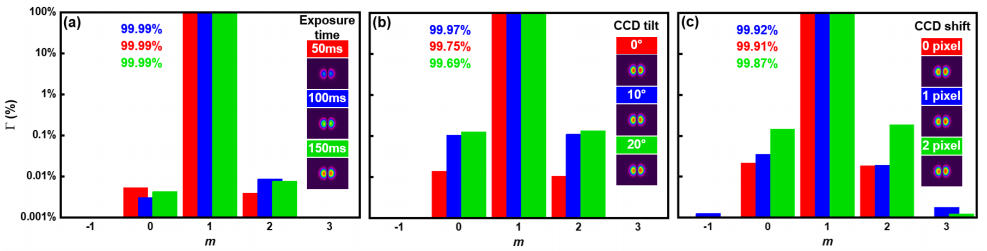
实验误差对结果的影响

三个误差导致测量的模式纯度0.1%至0.01%的偏差，但总体而言，实验结果表明，自干扰方法具有良好的鲁棒性。仔细的对准和优化的误差分析使我们能够生成和测量模式纯度高达99.99%的单个组件。

审核编辑：汤梓红