

脉冲信号频谱分析基础知识:脉冲波形的基本性质
描述
脉冲信号用于电子和无线电的各个领域。一个特殊的例子是在雷达信号中,但还存在许多其他应用。
鉴于它们的使用,通常需要使用频谱分析仪来测量信号的特性。然而,它们被脉冲的事实提出了一些有趣的挑战。
传统上,脉冲频谱分析技术和方法通常针对稳定的模拟射频信号。然而,脉冲频谱分析需要对所分析的信号有一点了解,这可以获得额外的信息。
射频脉冲信号或任何形式的脉冲信号有多种形式,但尽管种类繁多,但它们具有许多共同特征。这意味着可以应用常见的脉冲频谱分析技术。
要了解用于脉冲信号频谱分析的技术,首先需要了解脉冲波形的基本性质。它的重复时间为 T,脉冲持续时间为 t。
使用傅里叶分析可以看出,该波形由基波和谐波组成。方波的基本波形可以由与方波重复率相同的基波正弦波组成,然后是奇次谐波,谐波幅度与其数量成反比。
矩形脉冲只是这一基本原理的延伸。通过改变谐波的相对幅度和相位(奇数和偶数)来获得不同的波形形状。
脉冲波形由基波及其谐波组成
然后可以绘制这些基带信号,并绘制无限次谐波的幅度和相位,包括奇数和偶数,从而产生如下所示的平滑包络。
完美矩形脉冲的频谱
然后可以将该单波调制到射频波形上以提供频谱。随着基带信号的谐波延伸到无穷大,调制信号的边带也延伸到无穷大。然而,在现实中,带宽永远不会是无限的,谐波,尤其是高阶谐波会衰减。虽然这会导致信号失真,但电平通常是可以接受的。
调制到具有相位反转的射频载波上的脉冲波形频谱
脉冲频谱分析
已经可以看到脉冲信号是如何产生的,以及由此产生的光谱。虽然边带的相位在上图中得到了调整,但频谱分析仪是标量测试仪器,通常不会指示信号的相位。因此,频谱分析仪的绘图仅显示“在线上方”。
调制到射频载波上的脉冲波
形的标量频谱,即仅包括幅度。
为此,可以注意以下几点:
光谱线:调制波形图上显示的各个频谱线之间相隔的频率等于 1/T。
信封中的空值:光谱包络或整体形状中的零点以 1/t 的间隔出现。在n / t处出现进一步的零点
包络零清晰度:由于调制信号的上升和下降时间有限,并且存在由此产生的不对称性,因此脉冲频谱形状中的零点并不总是特别明显。
脉冲脱敏
有时,脉冲脱敏问题在脉冲频谱分析中会提到。问题在于,当调制施加到载波时,包络的峰值电平会降低,似乎信号的总功率已经降低。
峰值幅度明显降低是因为将脉冲添加到信号中并用方波调制会导致功率在载波和边带之间分配。随着调制电平的增加,边带电平也会增加。由于可用的功率有限,并且每个频谱分量(即载波和边带)仅包含总功率的一小部分。
在频谱分析仪上看到的总体效果是峰值功率降低,但它分布在更宽的带宽上。
可以α定义脉冲脱敏因子。这可以用等式来描述:
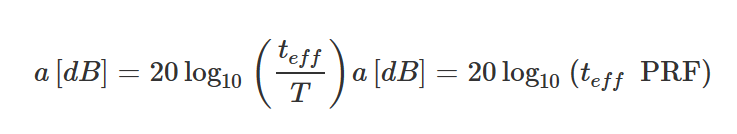
应该注意的是,这种关系只对真正的傅里叶线谱有效。为此,分析仪的分辨率带宽应<0.3 PRF。
信号的平均功率还取决于占空比,因为只有当信号处于可以粗略地称为“ON”状态时,才能辐射功率。这可以通过以下公式定义:
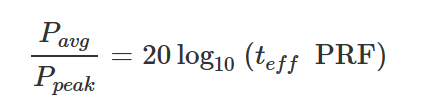
其中:
α = 脉冲“衰退因子
T = 脉冲重复率
PRF = 脉冲重复频率 (1 / T)
t = 脉冲长度 teff = 有效脉冲长度
,考虑上升和下降时间
Pavg = 脉冲周期
内的平均功率 Ppeak = 峰值功率
三角形和梯形波形
虽然脉冲频谱分析通常应用于方波或矩形波形,但类似的原理也适用于三角形和梯形波形。
波形的格式与脉冲波形具有许多相似的特征,但具有不同组成信号的电平,因此具有不同的边带。
因此,可以以类似的方式分析这些波形。
脉冲频谱分析测量技巧
当使用频谱分析仪查看脉冲信号时,有必要采用技术来确保显示信号以揭示所需的方面。
一些主要方面是:
小于行距的测量带宽:为了分辨单个谱线,测量带宽必须相对于谱线的偏移量很小,即带宽< 1 / T。如果测量带宽进一步降低,它们谱线将保留其值(如预期的那样),但噪声水平将降低,尽管测量时间会更长。
行距和零点间距之间的测量带宽:当测量带宽大于光谱线间距但小于零点间距时,将发生下一阶段。在这种情况下,谱线无法分辨,包络的振幅高度取决于带宽。这是因为更多的光谱线,每条都有自己的功率贡献,包含在测量带宽内。对于这种情况,1 / t > B > 1 / T。
大于零点间距的测量带宽:对于测量带宽大于信号频谱包络上的零点间距(即 B > 1 / T)的情况,无法识别信号的幅度分布。
随着脉冲传输的广泛应用,脉冲频谱分析是表征和测试任何开发的设备及其产生的信号的重要元素。
审核编辑:黄飞
-
4052E信号频谱分析仪2025-06-17 506
-
是德频谱分析仪对脉冲信号的测量方法2024-11-26 2078
-
4052系列信号/频谱分析仪概述2024-09-21 1402
-
频谱分析仪入门指南:基础知识详解2024-03-06 2516
-
USB频谱分析仪基础知识2024-01-16 1060
-
安捷伦频谱分析仪的基本知识2021-09-02 3575
-
如何用泰克高端示波器和频谱分析仪,来分析雷达脉冲信号2020-03-03 2741
-
Chirp脉冲波形的性能参数对脉冲频谱的影响介绍2019-06-14 2839
-
脉冲信号是什么_脉冲波是什么2017-11-14 48365
-
脉冲激光器对金属中激光超声信号的频谱分析2017-10-19 1278
-
脉冲波形的产生和整形与基本知识2017-09-19 868
-
基于频谱分析恒虚警技术的脉冲多普勒引信2016-12-24 863
-
脉冲波形的产生与变换2009-12-09 1035
-
信号频谱分析和测试2009-06-22 6547
全部0条评论

快来发表一下你的评论吧 !

