一文详解散射场与ISAR成像

成像原理

理想导体的散射场可表示为

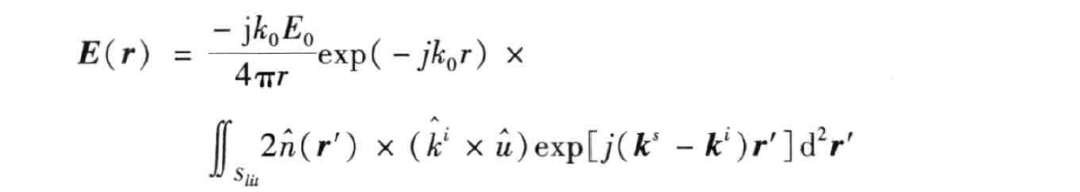
式中：  和  分别是入射波和散射波的波数矢量；  为入射表面的法向矢量；  为入射波方向的单位矢量；  和  分别是入射波的幅度和极化单位矢量；  为电磁波所照射的目标表面。

设雷达天线接收的是  方向极化的散射场，则上式可写为

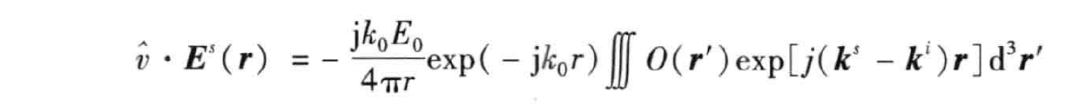
式中，  是目标形状方程标量表示，即

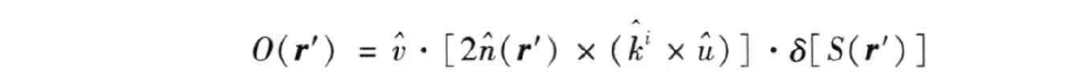
式中，  定义为

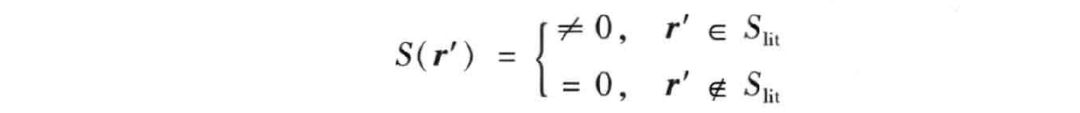
的三维傅里叶变换为

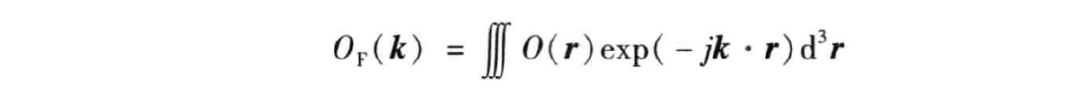
因此，  方向上的散射电场可写为

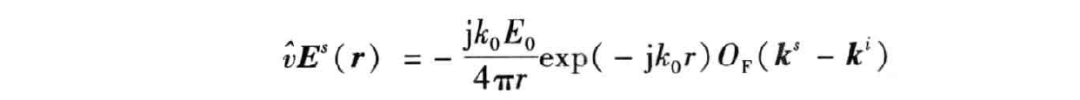
可见目标的散射电场正比于其  的三维傅里叶变换，这是 ISAR 成像的理论基础。需要指出的是，  随着雷达视角和雷达频率的变化而变化。

一维距离像

ISAR 图像可以看作是目标在二维（距离-横向）平面上距离和方位轮廓的显示。因此，在理解 ISAR 图像的含义之前，了解距离轮廓和方位轮廓的意义至关重要。

距离轮廓是从目标返回的波形形状。如果波束是时域脉冲，则接收信号将具有一维特性，通常是场强（或雷达截面积）与时间（或距离）的关系，如下图所示。如果波束是阶跃频率波形，则接收信号的 IFT 表征了目标的一维距离轮廓。

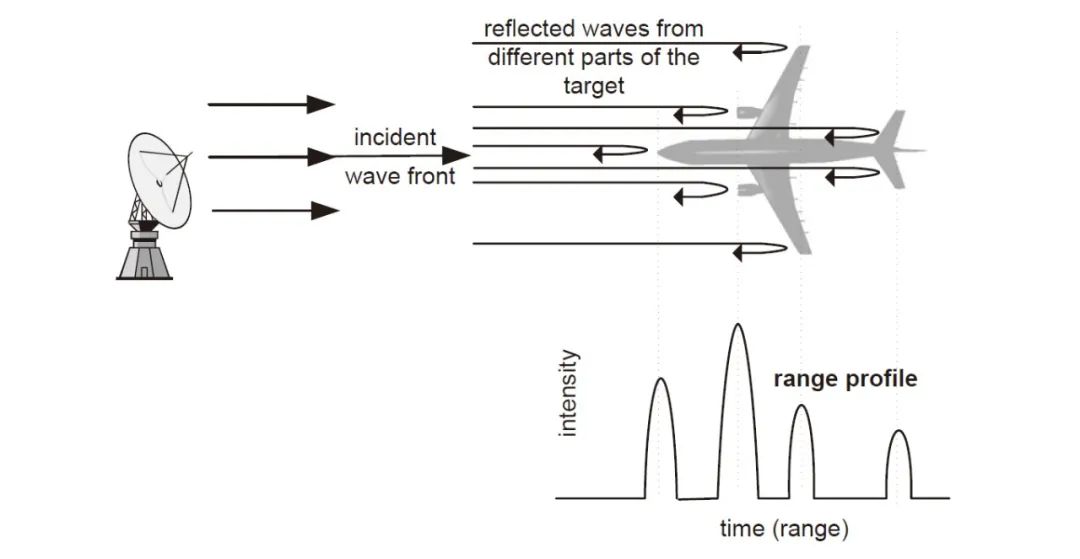
距离轮廓的物理意义通过上图中的飞机距离轮廓图的案例得到阐明：当入射波形入射目标时，一些能量将以目标为中心反射回雷达。如果这些散射中心与雷达的距离不同，它们将在不同的时刻返回到雷达接收器，以便在相应的一维距离剖面中区分它们。

如上图所示，后向散射点的来源可能位于驾驶舱、引擎、机翼、机尾或飞机的其他一些点上。当然，不可能通过利用距离轮廓概念来解决同一距离的散射中心，因为它们显示在相同的距离箱（或时间位置）中。

假设有  个散射点，每个散射点位于距离r。处，因此在远场假设下，其散射电场为

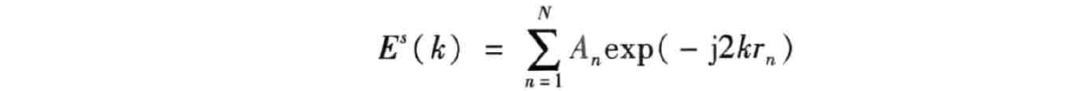
式中，  是位于距离  处点目标后向散射电场的幅度；  是对应频率  的波数，  。假设场景的相位中心位于  处，那么通过对上式进行傅里叶变换即可获得目标的距离像，即

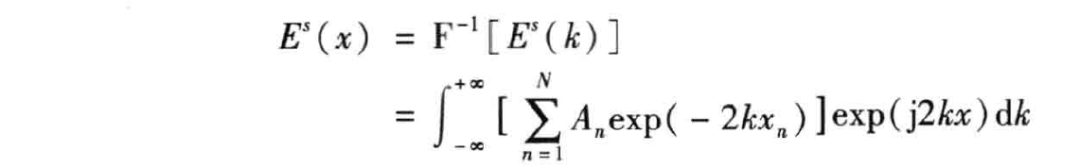
亦可写为

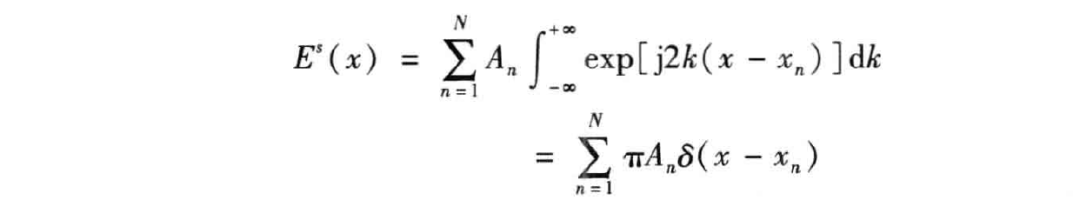
实际应用中，频率不可能为无限大，即  一般限制在一个波数范围之内，因此上式可写为

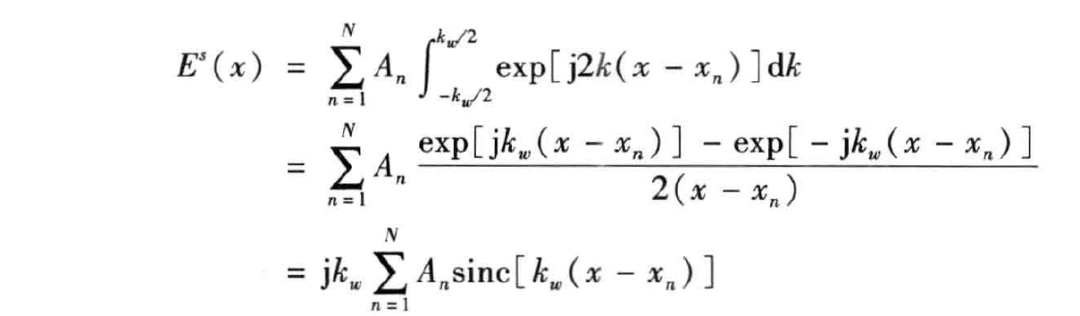
其中  ，  为信号频率域带宽。  函数表达了目标在距离像中的形状。  表明第  个散射中心在距离像中以  为中心，  为幅度。

根据傅里叶理论，在有限带宽的情况下，目标发生散焦是不可避免的。根据上式，可知距离向分辨率  满足  ，因此距离向分辨率可表达为

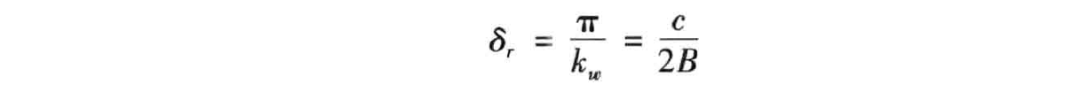
一维方位像

距离像是通过处理来自目标的频率分集的雷达信号获取的，同样地，方位像可以通过收集目标在不同视角下回波信号得到。

在方位维处理中，需要做的事情是分开位于同一个距离单元内处于不同方位向的散射点。在 ISAR 观测过程中，目标相对于雷达转过的视角宽度决定了目标的方位向分辨率。

假设有  个散射点分别位于  ，其中  代表距离坐标，  代表方位向坐标。计算方位像的目的是区分不同散射点在方位像上的位置，即测量每个目标的方位像坐标  。

在不同视角下，远场目标的散射电场可近似为

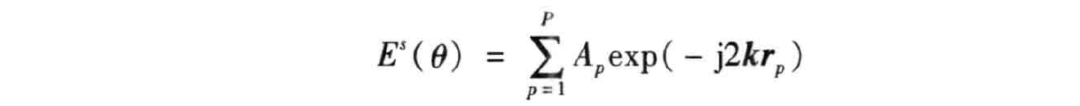
式中，  是第  个散射点的散射场幅度；  是目标中心点到  点的矢量；  是相对入射方向的波数矢量，且

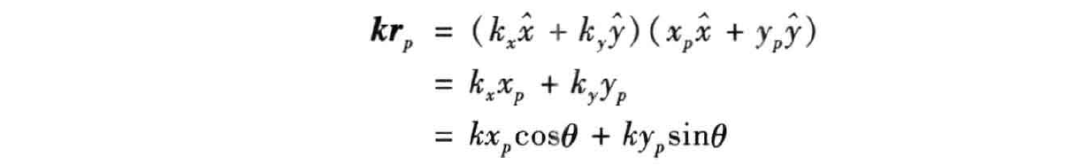
因此，散射场表达为

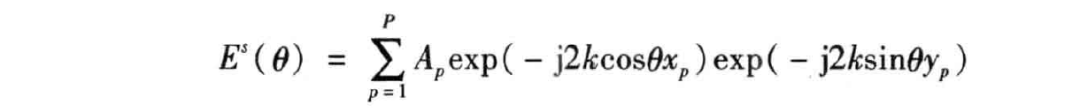
远场情况下，视角变化  较小，可近似认为  ，  ，因此散射场也可以近似表达为

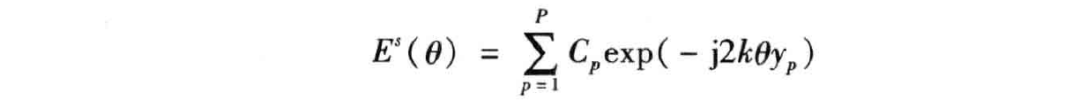
式中，  为常数，  。可见  与  之间存在傅里叶变换的关系。因此通过对上式取一维傅里叶变换，即可得到  的分布，即

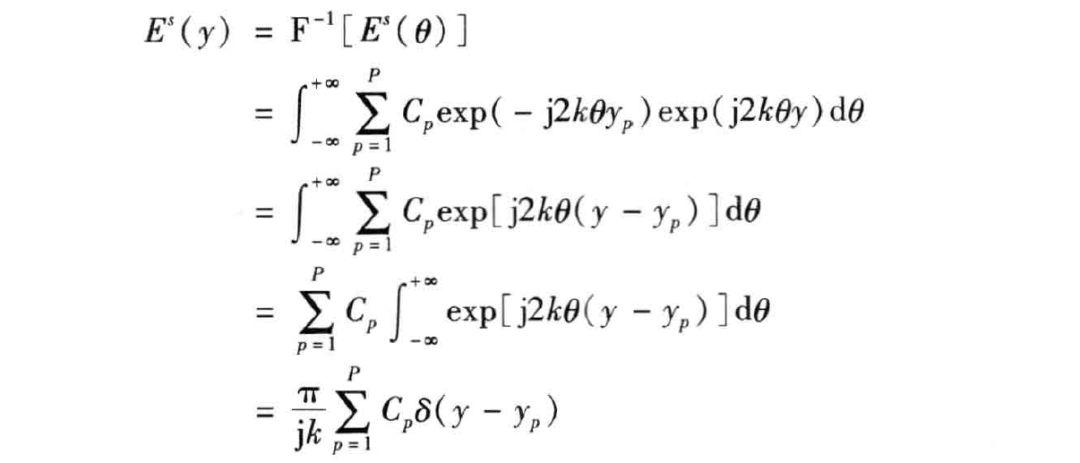
实际工程应用中，视角  不可能为无穷大，只能在某个角度范围  内变化，因此  实际上表达为

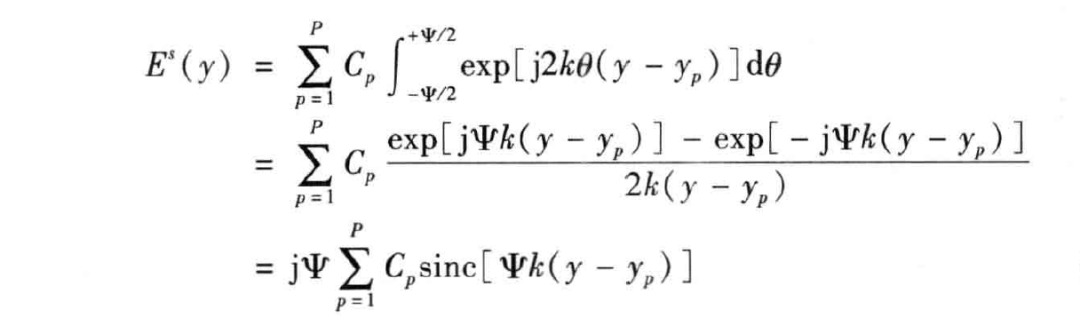
从上式可以看出，方位分辨率  满足  ，因此有

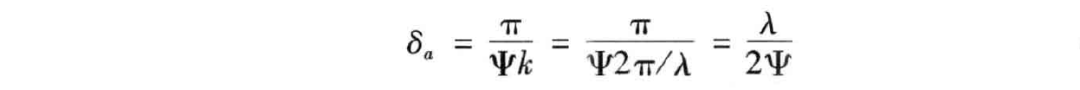
即 ISAR 图像的方位向分辨率同目标在观测过程中转过的视角宽度成反比。

审核编辑：黄飞