机器人运动学中的非完整约束与运动模型推导

动力学与运动学

机器人的动力学描述了作用在机器人上的力与机器人物理状态的变化之间的关系。例如，自动驾驶汽车的动力学将描述加速度和由轮胎、重力、空气动力学等引起的力之间的关系。

机器人的运动学描述了对机器人运动的不由力引起的额外的限制或约束。例如，具有多个关节的机械臂受到运动学约束，因为每个关节上的刚性连接只允许绕单个轴旋转。

机器人或自动驾驶车辆都要综合考虑动力学和运动学，某些情况 为了简化运算，在不追求精确的情况下，动力学和运动学都有可能被简化考虑。比如有些情况，车会被简化为一个质点，等等情况。

运动学约束

1. 广义坐标

广义坐标指的是一组可以完全指定机器人的唯一位置的坐标。广义，顾名思义，这个坐标中的值除了我们熟知的x、y、z，也可能包括其他状态量，是一个泛泛的坐标概念。

2. 运动学约束

机器人运动学中的运动学约束是指机器人在运动过程中受到的限制，包括位置、姿态、速度和加速度等因素。这些约束会对机器人的自由度产生影响，从而影响机器人的运动和控制。运动学约束通常用数学模型来描述，为机器人的运动控制提供了理论基础。

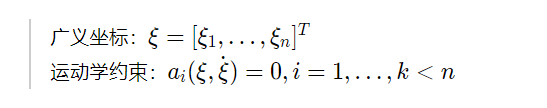
针对n维的广义坐标，他的运动学约束一定是小于n的（不然，大于等于n，方程直接求解了，还运动啥。。。）。

Pfaffian约束（普法夫约束）是一种特殊的运动学约束，Pfaffian约束是由k个线性无关约束的集合，且这些约束相对于广义速度是线性的约束。

3. 完整约束和非完整约束(Holonomic and Nonholonomic Constraints)

当运动学约束函数中只包含广义坐标（不依赖广义速度）的函数，就是一个完整约束。满足完整约束的系统就是一个完整系统。完整约束系统可以表达为

不能用上式表示的系统，就是一个非完整系统。完整系统的完整约束方程与位置、时间有关，与速度无关。

非完整系统主要表现特征是存在不可积分的微分约束。非完整约束系统的表达式如下：

完整约束限制了广义坐标的全部值，如果系统的每个状态均用广义坐标来表示的话，完整约束实际上限制的，就是系统可以达到的全部有效状态。

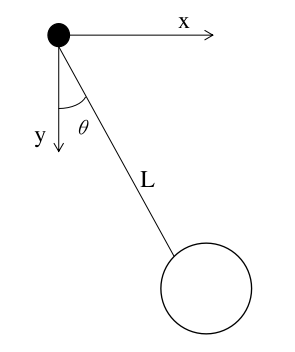
不太好理解，需要我们结合几个例子来简单了解一下就可以了：一个单摆系统，在无外力干扰的情况下，摆锤的广义坐标只有x和y，它们的值会一直满足一个圆弧的约束，且与速度无关，所以单摆系统就是一个完整系统，满足一个完整约束。

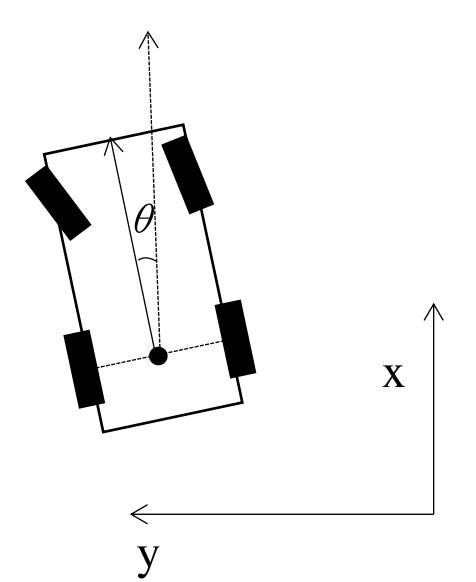
一个简单移动机器人系统，它的广义坐标为（x, y, θ），在理想情况下该机器人不可以发生平移。不能平移的条件就是，车轮在横向方向的速度为0。它是一个普法夫约束，但该普法夫约束不能积分为完整约束，所以该系统是一个非完整系统，具备非完整约束。

完整约束就是状态之间的到达没有限制，而非完整约束就是状态间的到达必须满足一些固定条件

总之，如果机器人约束方程中包含坐标对时间的导数(如运动约束)，而且方程不可能积分为有限形式，这类约束称为非完整约束。非完整约束方程总是微分方程的形式。反之，如果机器人约束方程中不包含坐标对时间的导数，或者约束方程中的微分项可以积分为有限形式，这类约束称为完整约束。

运动学模型

运动学模型的方程组，实际上就是描述了状态的微分量与控制量的关系，每一次的控制量作用于该系统能带来状态量多少改变。而它们之间的那个变化关系，是与系统的约束相关的。

式子中，v就是车辆的速度，w就是车辆旋转的角速度。发没发现，其实这个运动学公式我们本可以直接写出，但我们通过约束方程推出了相同的结论。