

基本模拟运算放大器积分器电路设计
模拟技术
描述
运算放大器是模拟积分器电路的理想基础。输入电流几乎为零,输出电压构成输入信号的精确积分。
虽然仅使用电阻器和电容器就可以开发一个简单的积分器电路,但运算放大器可以实现更好的性能,即获得更真实的集成。
在大多数运算放大器电路中,使用的反馈本质上主要是电阻性的,直接电阻路径至少形成网络的一部分。然而,对于积分器来说,情况并非如此 - 在运算放大器的输出和输入之间提供反馈的元件是一个电容器。
顾名思义,运算放大器积分器执行的功能相当于数学积分函数的电子功能。事实上,电子积分器电路可用于模拟计算机。
就其工作而言,电路产生的输出与其输入电压相对于时间的积分成正比。
这意味着任何时候的输出电压都由起始输出电压、输入电压存在的时间长度和输入电压的值决定。
积分器电路背后的基本思想如下所示。尽管运算放大器积分器电路有一些变化,但这个概念是其工作背后的原因。
积分器电路的波形
从图中可以看出,虽然输入保持为零,但输出也保持为零。但是,当向输入端施加阶跃输入电压时,输出会上升。当阶跃输入返回到零时,输出保持在上次达到的电压。
运算放大器积分器电路
基本运算放大器积分器电路由一个运算放大器组成,输出和反相输入之间有一个电容,以及一个从反相输入到整个电路输入的电阻器,如图所示。
基本模拟运算放大器积分器电路
首先要注意的一点是,当信号施加到反相输入端时,电路的输出是基本CR积分器网络的逆输出。
运算放大器积分器电路的波形 注意:输出的反相,因为输入施加到运算放大器反相输入
运算放大器积分器设计计算
电路所需的主要计算是确定给定输入电压在给定时间内的输出电压。
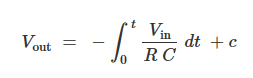
其中:
Vout = 运算放大器积分器的输出电压 Vin = 输入电压 T = 开始施加电压后的时间(以秒为单位) R = 积分器
中的电阻值(以Ω为单位)
C = 积分器电容器的电容(法拉) c = 积分常数,在本例中为输出起始电压。
公式中的负号反映了使用运算放大器的反相输入导致的反相。
运算放大器饱和度
很明显,积分器的输出不能无限上升,因为输出将受到限制。
运算放大器积分器的输出将受到电源或电源轨电压以及运算放大器本身的饱和度的限制,即输出可以摆动到离电源轨的距离。
在设计其中一个电路时,可能需要限制增益或增加电源轨电压,以适应可能的输出电压摆幅。
虽然小输入电压和短时间可能是可以接受的,但在设计电路时必须小心,因为输入电压可以保持较长时间。
显示饱和点的运算放大器模拟积分器
积分器复位能力
有时需要有一种方法可以将运算放大器积分器复位为零。
添加复位设施或功能非常容易实现。只需在积分器电容两端添加一个开关即可实现。这具有使电容器放电的效果,从而使整个积分器复位。
带复位开关的模拟运算放大器积分器电路
复位开关可以通过多种方式实现。显然可以使用简单的机械开关,但也可以使用半导体开关。这些通常是基于 FET 的开关,因为它们具有非常高的关断电阻,并且可以在此类应用中更轻松地作为开关进行控制。
运算放大器积分器电路可以精确地对要获得的输入信号进行积分。该电路已用于许多模拟计算机,如今,许多模拟应用都需要集成功能,其中运算放大器电路是理想的解决方案。
审核编辑:黄飞
-
运算放大器的主要应用与硬性要求2022-08-25 3584
-
在由运算放大器构成的积分器中,积分电容因该选什么类型的电容?2024-09-24 647
-
运算放大器积分电路分析2025-03-11 743
-
运算放大器权威指南和基于运算放大器和模拟集成电路的电路设计及OP放大器应用技巧100例PDF分享2017-06-09 106144
-
基于运算放大器和模拟集成电路的电路设计资料分享!2019-08-19 10672
-
一文清晰概述积分运算放大器的电路设计2021-01-04 12544
-
运算放大器的各项模拟积分器电路应用有哪些?2021-03-11 2222
-
采用运算放大器的积分器电路分析2021-04-06 1324
-
请大佬详细分析一下采用运算放大器的积分器电路?2021-04-12 1486
-
反相积分运算电路2008-09-22 36324
-
基于Labview的集成运算放大器虚拟实验2011-07-04 1254
-
如何使用运算放大器实现各项模拟积分器的应用电路说明2020-11-20 1729
-
运算放大器的基本电路有哪些2023-04-24 8599
-
基于运算放大器的积分器电路实验过程2023-07-20 5633
-
运算放大器积分电路设计2024-10-29 7680
全部0条评论

快来发表一下你的评论吧 !

