

深入了解浮点运算—CPU和GPU算力是如何计算的?
描述
随着国家大力发展数字经济,算力的提升和普惠变得越来越重要。在数字化时代,算力已成为推动科技发展和创新的关键要素。它不仅仅是衡量计算机处理速度的标准,还涉及计算机系统或设备执行计算任务的能力、数据处理能力以及解决复杂计算问题的能力。那么算力到底是什么呢?
简单了解算力
算力(Computational Power)在计算机科学和计算领域中是一个重要概念,它指的是计算机系统或设备执行数值计算和处理任务的能力。提升算力意味着可以更快地执行复杂的计算任务,从而提高计算的效率和性能。简单来说,算力决定了计算机处理信息的速度和效率,直接影响我们使用电子设备的体验,例如网页加载速度和游戏流畅度等。
在数字经济时代,算力是新的生产力,为加强数字政府建设、激活数据要素潜能以及实现各行各业的数字化转型提供了动力。据中国信息通信研究所的测算,每投入1元的算力,可以带动3至4元的经济产出。算力的提升对经济具有巨大的影响力。根据统计数据显示,每提高一个算力指数点,可以带动数字经济增长 0.36% 和 GDP 增长 0.17%。
那算力大小具体是如何衡量的呢?这里就必须提及浮点运算,接下来我们来了解下浮点运算这个概念。
什么是浮点运算
算力最基本的计量单位是 FLOPS,英文 Floating-point Operations Per Second,即每秒执行的浮点运算次数。浮点运算其实就是带小数的加减乘除运算。
举个例子:1.1+2.2 就是典型的浮点运算,估计你已经心算出结果是 3.3 了。不过对计算机来说,这个问题并不简单。我们知道,计算机是以 0 和 1 构成的二进制数字进行运算的,比如在基础的二进制里,1 就是 1,2 就变成了 “10”,3 是 “11”,这也带来一个问题:计算机能够处理的数字只有整数。
其实,0.1 可以看成是1除以10的结果,我们想让计算机计算一个带小数点的数字,只要告诉 CPU 这是一个被 1 后面加了多少个 0 整除的整数就行了。这样一来,计算机在处理小数点的时候,就多了好几个运算步骤。浮点运算的速度也就成了衡量计算机性能的标准。
算力的计量单位,除了 FLOPS,从小到大还有:
KFLOPS(每秒1000次浮点运算,10^3)
MFLOPS(每秒1百万次,10^6)
GFLOPS(每秒10亿次,10^9)
TFLOPS(每秒1万亿次,10^12)
PFLOPS(每秒1000万亿次,10^15)
EFLOPS(每秒100亿亿次,10^18)
浮点数
浮点数的浮点就是指它的小数点的位置是可以是漂浮不定的。这怎么理解呢?其实,浮点数是采用科学计数法的方式来表示的,例如十进制小数 1.234,用科学计数法表示,可以有多种方式:
1.234 = 1.234 * 10^0 1.234 = 12.34 * 10^-1 1.234 = 123.4 * 10^-2 ...
用这种科学计数法的方式表示小数时,小数点的位置就变得漂浮不定了。使用同样的规则,对于二进制数,我们也可以用科学计数法表示,也就是说把基数 10 换成 2 即可。那浮点数如何表示数字?其实浮点数是采用科学计数法来表示一个数字的,它的格式可以写成这样:
V = (-1)^S * M * R^E
其中各个变量的含义如下:
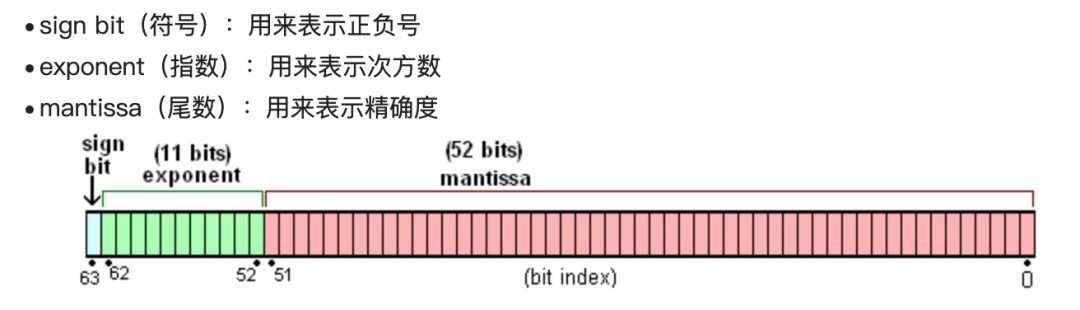
S:符号位,取值 0 或 1,决定一个数字的符号,0 表示正,1 表示负
M:尾数,用小数表示,例如前面所看到的 1.234 * 10^0,1.234 就是尾数
R:基数,表示十进制数 R 就是 10,表示二进制数 R 就是 2
E:指数,用整数表示,例如前面看到的 10^-1,-1 即是指数
如果我们要在计算机中,用浮点数表示一个数字,只需要确认这几个变量即可。
举个例子:将十进制数 0.125 转换为浮点数,我们可以使用二进制浮点数表示。
符号位(S):由于数字为正数,所以 S = 0。
尾数(M):将小数部分转换为二进制。0.125 的二进制表示为 0.001。
基数(R):对于二进制数,R = 2。
指数(E):确定指数的值。将 0.125 转换为科学计数法形式可得 0.125 = 1.0 * 2^-3。因此,指数 E = -3。
代入公式:V = (-1)^S * M * R^E
将以上值代入公式可得:
V = (-1)^0 * 0.001 * 2^-3 = 0.001 * 0.125
运算结果为 0.000001。因此十进制数 0.125 在二进制浮点数表示下为 0.000001。
计算机中使用有限的连续字节来保存浮点数,而 IEEE 754标准定义了三种常见的浮点数格式:单精度、双精度和扩展双精度,它们适用于不同的计算需求。一般来说,单精度适合一般计算,双精度适合科学计算,扩展双精度适合高精度计算。一个遵循 IEEE 754标准的系统必须支持单精度类型(强制类型),最好也支持双精度类型(推荐类型),而扩展双精度类型则是可选的。
单精度浮点数(FP32)
单精度浮点数格式(英语:single-precision floating-point format)是一种数据类型,在计算机存储器中占用 4 个字节(32 bits),利用 “浮点”(浮动小数点)的方法,可以表示一个范围很大的数值。在 IEEE 754-2008 的定义中,32-bit base 2 格式被正式称为 binary32 格式。这种格式在 IEEE 754-1985 被定义为 single,即单精度。需要注意的是,在更早的一些计算机系统中,也存在着其他 4 字节的浮点数格式。
第 1 位表示正负,中间 8 位表示指数,后 23 位储存有效数位(有效数位是 24 位)。第一位的正负号 0 代表正,1 代表负。中间八位共可表示 2^8 = 256 个数,指数可以是二补码;或 0 到 255,0 到 126 代表 -127 到 -1,127 代表零,128-255 代表 1-128。有效数位最左手边的 1 并不会储存,因为它一定存在(二进制的第一个有效数字必定是1)。换言之,有效数位是 24 位,实际储存 23 位。
举个例子:要将十进制数 0.125 转换为单精度浮点数(32 位)。
遵循 IEEE 754 标准的表示方法,可以按照以下步骤进行转换:
符号位(Sign):由于数字为正数,所以符号位为 0。
尾数(Fraction):将小数部分转换为二进制。0.125 的二进制表示为 0.001。
指数(Exponent):指数的偏移量为 127。由于 0.125 可以表示为 1.0 × 2^(-3),指数为 -3。加上偏移量后,实际指数为 -3 + 127 = 124。将 124 转换为二进制得到 01111100。
组合位:将符号位、指数位和尾数位组合在一起,得到单精度浮点数的二进制表示。
最终的二进制表示为:0 01111100 00100000000000000000000
双精度浮点数(FP64)
双精度浮点数(Double Precision Floating Point),也称为 FP64,是一种浮点数数据类型,用于在计算机中表示和进行高精度的浮点数运算。FP64 使用 64 个比特位(8 个字节)来表示一个浮点数,其中 1 位用于表示符号位(正负号),11 位用于表示指数,52 位用于表示尾数。
双精度浮点数的表示形式同样采用科学计数法,即 ±M × 2^E,其中 M 为尾数,E 为指数。通过使用更多的指数位和尾数位,FP64 相对于单精度浮点数能够表示更广范围和更高精度的数值。
举个例子:将十进制数 0.125 转换为双精度浮点数(64位)。
遵循 IEEE 754 标准的表示方法,可以按照以下步骤进行转换:
符号位(Sign):由于数字为正数,所以符号位为 0。
尾数(Fraction):将小数部分转换为二进制。0.125 的二进制表示为 0.001。
指数(Exponent):指数的偏移量为 1023。由于 0.125 可以表示为 1.0 × 2^(-3),指数为 -3。加上偏移量后,实际指数为 -3 + 1023 = 1020。将 1020 转换为二进制得到 01111111100。
组合位:将符号位、指数位和尾数位组合在一起,得到双精度浮点数的二进制表示。
最终的二进制表示为:0 01111111100 0010000000000000000000000000000000000000000000000000
双精度浮点数的取值范围约为 ±4.9 × 10^-324 到 ±1.8 × 10^308,并提供大约 15 到 16 位有效数字的精度。相比于单精度浮点数,双精度浮点数能够处理更大范围的数值和提供更高的精度,适用于对精确性要求较高的计算任务。
双精度浮点数常用于科学计算、工程应用、金融分析和高性能计算等领域。它在这些领域中被广泛用于处理实数数据,如数值模拟、大规模计算、天文学、物理学和工程计算等。
然而,需要注意的是,双精度浮点数的存储空间和计算开销相对于单精度浮点数更高。在某些情况下,如果对精度要求不高或者计算资源有限,可以考虑使用单精度浮点数进行计算,以提高计算效率和节省内存消耗。
浮点数的舍入
由于浮点数计算过程中丢失了精度,浮点运算的性质与数学运算有所不同。任何有效数上的运算结果,通常都存放在较长的寄存器中,当结果被放回浮点格式时,必须将多出来的比特丢弃。IEEE 标准列出 4 种不同的方法:
舍入到最接近:舍入到最接近,在一样接近的情况下偶数优先(Ties To Even,这是默认的舍入方式):会将结果舍入为最接近且可以表示的值,但是当存在两个数一样接近的时候,则取其中的偶数(在二进制中是以0结尾的)。
朝 +∞ 方向舍入:会将结果朝正无限大的方向舍入。
朝 -∞ 方向舍入:会将结果朝负无限大的方向舍入。
朝 0 方向舍入:会将结果朝 0 的方向舍入。
单、双精度的应用场景
单精度浮点数通常应用在需要较高计算速度的场景,例如嵌入式系统和移动设备。在这些应用中,对于一些实时性要求较高的任务,如图形渲染、音视频处理等,单精度浮点数能够提供足够的精度,并且在存储和计算上更加高效,能够满足实时性和资源限制的需求。此外,单精度浮点数也广泛应用于科学研究和工程领域中的数值计算,包括求解方程、模拟物理过程等。在这些领域中,单精度浮点数的精度已经足够满足大部分的计算需求,同时可以提高计算速度和节省存储空间。
双精度浮点数主要应用于需要更高精度的场景,如科学计算、工程计算、金融分析等。在这些领域中,对计算结果的精确性要求较高,需要更多的有效数字来表示和处理实数。双精度浮点数能够提供更高的精度和更大的表示范围,能够处理更复杂和精细的计算任务。在科学计算中,如天文学、数值模拟等领域,双精度浮点数常常用于求解复杂的数学模型和算法,以获得更准确的结果。在金融分析中,双精度浮点数可以处理更大的数值范围和更高的精度,确保计算结果的准确性和可靠性。
总之,选择单精度还是双精度浮点数应根据具体应用的需求来决定,需要权衡计算速度、精度要求和资源限制等因素。单精度浮点数适用于对计算速度要求较高且精度要求不是特别严格的场景,而双精度浮点数适用于对精度要求更高的科学计算和工程领域。
CPU 和 GPU 的算力计算
目前服务器的算力主要包括 CPU 和 GPU 等不同芯片产生的算力。那具体到每台服务器的算力,究竟如何计算呢?
CPU 的算力计算
我们以 CPU 的双精度浮点运算能力(FP64)为例,单个 CPU 的算力,与 CPU 核心的个数、频率、单时钟周期浮点计算能力 3 个因素有关。
单 CPU 算力 = CPU 核数 * 单核主频 * 单周期浮点计算能力
以 Intel Cascade Lake 架构的 Xeon Platinum 8280 为例,该 CPU 具有 28 个核心,主频为 2.7GHz,并支持 AVX512 指令集。根据提供的信息,我们可以计算出该 CPU 的双精度浮点运算能力(FP64)。
首先,计算单个 CPU 核心的单周期浮点计算能力:
单周期浮点计算能力 = 512bit * 2FMA * 2M/A / 64bit = 32 FLOPS/Cycle
然后,计算单个 CPU 核心的峰值浮点运算能力:
单个 CPU 核心的峰值浮点运算能力 = 单周期浮点计算能力 * 主频 = 32 FLOPS/Cycle * 2.7 GHz
最后,计算整个 CPU 的峰值浮点运算能力:
单 CPU 算力 = CPU 核数 * 单个 CPU 核心的峰值浮点运算能力 = 28 cores * 单个CPU核心的峰值浮点运算能力
根据提供的数据,计算得到:
单个 CPU 核心的峰值浮点运算能力 = 32 FLOPS/Cycle * 2.7 GHz = 86.4 GFLOPS
单 CPU 算力 = 28 cores * 86.4 GFLOPS = 2.4192 TFLOPS
因此,以 Intel Cascade Lake 架构的 Xeon Platinum 8280 为例,该 CPU 的理论峰值双精度浮点性能为 2.4192 TFLOPS。
注:该计算是理论值,实际性能可能受到多种因素(如指令级并行性、内存访问延迟等)的影响。
GPU 的算力计算
GPU 的算力与上面的计算方法类似。单个 GPU 算力也是与核心个数、频率、单时钟周期能力 3 个因素有关。
以 NVIDIA Volta 架构的 V100 为例,该 GPU 拥有 2560 个双精度浮点核心(FP64 cores),主频为 1.530GHz。
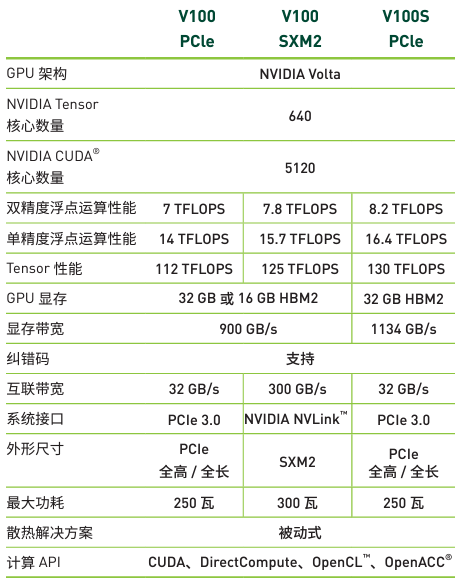
根据提供的信息,我们可以计算出该 GPU 的双精度浮点运算能力(FP64)。
首先,计算单个 GPU 核心的单周期浮点计算能力:
单周期浮点计算能力 = 64bit * 1FMA * 2M/A / 64bit = 2 FLOPS/Cycle
然后,计算单个 GPU 核心的峰值浮点运算能力:
单个 GPU 核心的峰值浮点运算能力 = 单周期浮点计算能力 * 主频 = 2 FLOPS/Cycle * 1.530 GHz
最后,计算整个 GPU 的峰值浮点运算能力:
单 GPU 算力 = GPU 核数 * 单个 GPU 核心的峰值浮点运算能力 = 2560 cores * 单个 GPU 核心的峰值浮点运算能力
根据提供的数据,计算得到:
单个 GPU 核心的峰值浮点运算能力 = 2 FLOPS/Cycle * 1.530 GHz = 3.060 GFLOPS
单 GPU 算力 = 2560 cores * 3.060 GFLOPS = 7833 GFLOPS = 7.833 TFLOPS
因此,以 NVIDIA Volta 架构的 V100 为例,该 GPU 的理论峰值双精度浮点性能为 7.833 TFLOPS。
注:该计算是理论值,实际性能可能受到多种因素(如内存带宽、功耗限制等)的影响。
聊了这么多,相信大家对 CPU、GPU 的算力计算和浮点运算都有了一定的了解,虽然看起来比较复杂,其实还是比较好理解的。大家也可以收藏下这篇内容,以备不时之需。
审核编辑:刘清
-
请问AURIX TC3xx tricore架构下浮点运算和将浮点数小数点去掉变成整数来计算哪种方式更加节省算力?2024-08-26 2135
-
名单公布!【书籍评测活动NO.43】 算力芯片 | 高性能 CPU/GPU/NPU 微架构分析2024-09-02 3685
-
【「算力芯片 | 高性能 CPU/GPU/NPU 微架构分析」阅读体验】--全书概览2024-10-15 2053
-
《算力芯片 高性能 CPU/GPU/NPU 微架构分析》第1-4章阅读心得——算力之巅:从基准测试到CPU微架构的深度探索2024-10-19 1636
-
【「算力芯片 | 高性能 CPU/GPU/NPU 微架构分析」阅读体验】--了解算力芯片CPU2024-10-20 1874
-
【「算力芯片 | 高性能 CPU/GPU/NPU 微架构分析」阅读体验】--了解算力芯片GPU2024-11-03 979
-
深入了解示波器2013-11-14 6142
-
CPU 的浮点运算能力比 GPU 差,为什么不提高 CPU 的浮点运算能力呢2018-03-16 16271
-
GPU是显卡吗 cpu和gpu哪个算力强2024-01-10 7918
-
算力系列基础篇——算力与计算机性能:解锁超能力的神秘力量!2024-07-11 104
-
算力服务器为什么选择GPU2024-07-25 2092
-
【一文看懂】大白话解释“GPU与GPU算力”2024-10-29 4482
-
云 GPU 加速计算:突破传统算力瓶颈的利刃2025-02-17 571
全部0条评论

快来发表一下你的评论吧 !

