

FPGA图像处理之CLAHE算法的线性差值
可编程逻辑
描述
CLAHE算法的线性差值。
我们先来看一下没有经过线性差值的CLAHE算法是什么样子的效果。
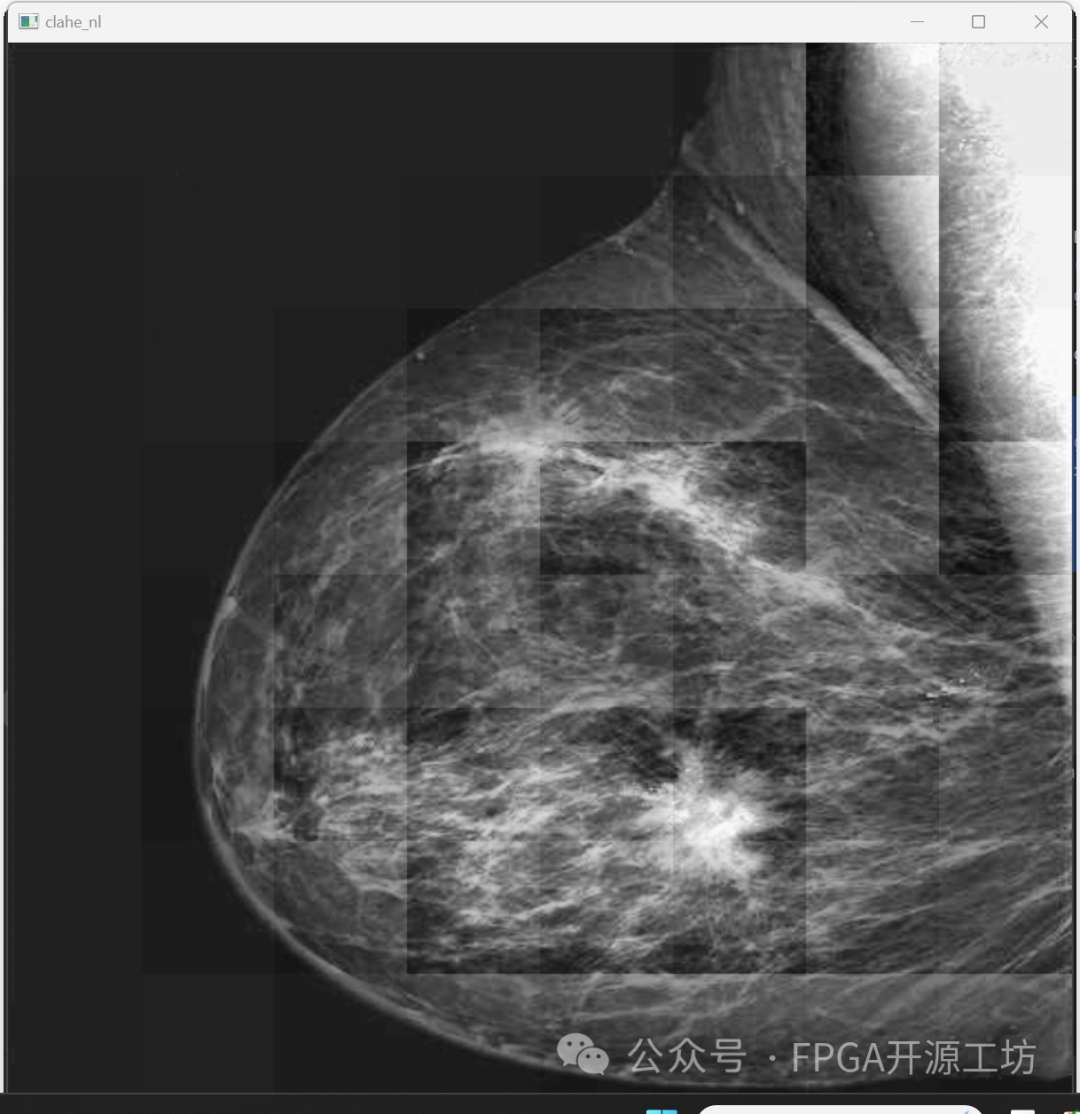
可以看到很明显的图片中都是一块一块的,这是因为在每一个块里面都统计了相应的直方图数据,这样就导致不同块里面直方图统计的映射表不一样,所以就出现了一块块的斑点。
解决这个问题的方法就是线性插值。
可以将整幅图像分为以下几个部分:

整个8*8一共64个block,然后对于四个红色的角点不进行线性插值,对于蓝色的四条边进行线性插值,对于中间的白色部分进行双线性插值。
其中红色正方形的边长是block边长的二分之一。
来放大一个局部看一下是怎样进行计算的,比如将左上角放大得到一个3*3的block,以黑色实线来表示每一个block。然后用蓝色虚线将每一个block的二分之一处进行连接,这样将每一个block都分成了4*4的小块。
最左上角的小块不进行线性插值,相应的代码如下,判断是不是在四个角点,如果是角点就直接进行直方图均衡化。
if i <= bh // 2 and j <= bw // 2:
he[i][j] = sk_list[0][img[i][j]]
elif i <= bh // 2 and j >= w - bw // 2:
he[i][j] = sk_list[block - 1][img[i][j]]
elif i >= h - bh // 2 and j <= bw // 2:
he[i][j] = sk_list[block * block - block][img[i][j]]
elif i >= h - bh // 2 and j >= w - bw // 2:
he[i][j] = sk_list[block * block - 1][img[i][j]]
第一个位于蓝色区域内的点,他需要进行线性插值才能得到最终的结果。
可以看到这个点位于第一个block中,假定他距离第一个block中线的距离是P,那么第一个block占的权重就是1-P/block_width,在第二个block中占的权重就是P/block_width。假如这个点正好在第一个和第二个block的交界处,那么两个block占的权重都是0.5。所以这个点的计算方法就是在第一个block中进行直方图均衡化得到的结果乘以第一个block的权重,加上在第二个block中进行直方图均衡化得到的结果乘以第二个block的权重。
比如下面的参考代码,先计算这个点位于哪一个block,然后计算相应的权重,最后分别进行直方图均衡化后把结果相加。
num_j = (j - bw // 2) // bw p = (j - num_j * bw - bw // 2) / bw q = 1 - p he[i][j] = sk_list[num_j][img[i][j]] * q + sk_list[num_j + 1][img[i][j]] * p
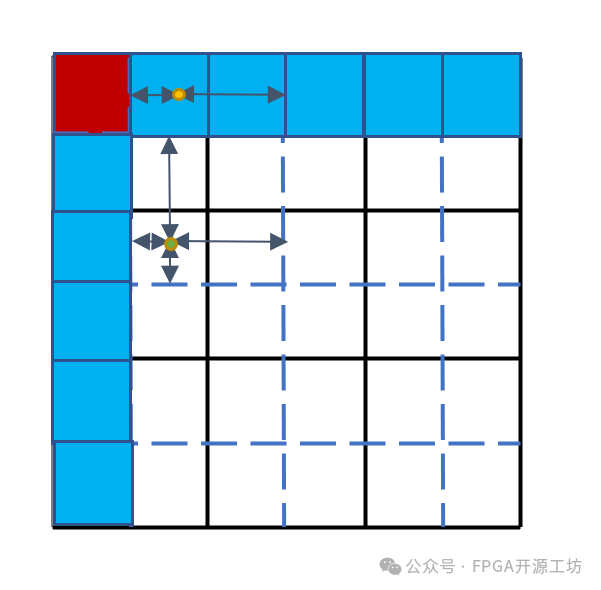
对于最后一种情况,也就是位于中间白色区域的点,他需要进行双线性插值。可以看到整个点位于第四个block,所以他需要在第一个,第二个,第四个和第五个block上分别计算直方图均衡化的结果,和相应的权重,参考代码如下:
num_i = (i - bh // 2) // bh
num_j = (j - bw // 2) // bw
m = (i - num_i * bh - bh // 2) / bh
v = 1 - m
p = (j - num_j * bw - bw // 2) / bw
q = 1 - p
he[i][j] = sk_list[num_i * block + num_j][img[i][j]] * q * v +
sk_list[(num_i * block) + block + num_j][
img[i][j]] * q * m + sk_list[num_i * block + num_j + 1][img[i][j]] * p * v +
sk_list[(num_i * block) + block + num_j + 1][img[i][j]] * p * m
对于verilog来说计算方法也是一样的,通过不同的点来分别计算结果。
case (switch_ff[23])
4'd0, 4'd1, 4'd2, 4'd3: begin
cand_tx_pipe_1[0] <= cand_rd_data_1_ff[21];
cand_tx_pipe_2[0] <= 28'd0;
cand_tx_pipe_3[0] <= 28'd0;
cand_tx_pipe_4[0] <= 28'd0;
end
4'd4, 4'd5: begin
cand_tx_pipe_1[0] <= cand_rd_data_1_ff[21] * q_ff[2];
cand_tx_pipe_2[0] <= cand_rd_data_2_ff[21] * p_ff[2];
cand_tx_pipe_3[0] <= 28'd0;
cand_tx_pipe_4[0] <= 28'd0;
end
4'd6, 4'd7: begin
cand_tx_pipe_1[0] <= cand_rd_data_1_ff[21] * v_ff[2];
cand_tx_pipe_2[0] <= cand_rd_data_2_ff[21] * m_ff[2];
cand_tx_pipe_3[0] <= 28'd0;
cand_tx_pipe_4[0] <= 28'd0;
end
4'd8: begin
cand_tx_pipe_1[0] <= cand_rd_data_1_ff[21] * q_ff[2];
cand_tx_pipe_2[0] <= cand_rd_data_2_ff[21] * q_ff[2];
cand_tx_pipe_3[0] <= cand_rd_data_3_ff[21] * p_ff[2];
cand_tx_pipe_4[0] <= cand_rd_data_4_ff[21] * p_ff[2];
end
default: begin
cand_tx_pipe_1[0] <= 28'd0;
cand_tx_pipe_2[0] <= 28'd0;
cand_tx_pipe_3[0] <= 28'd0;
cand_tx_pipe_4[0] <= 28'd0;
end
endcase
这里使用了DSP自动推断的方法,这些乘法都会被自动推断为DSP。
在计算之前对数据进行了打拍的操作,一部分寄存器会被DSP单元所吸收,所以不用担心这个乘法的时序问题。
always @(posedge clk ) begin
cand_rd_data_1_ff[0] <= cand_rd_data_1;
cand_rd_data_2_ff[0] <= cand_rd_data_2;
cand_rd_data_3_ff[0] <= cand_rd_data_3;
cand_rd_data_4_ff[0] <= cand_rd_data_4;
end
genvar b;
generate
for (b = 1; b <= 22; b = b + 1) begin
always @(posedge clk ) begin
cand_rd_data_1_ff[b] <= cand_rd_data_1_ff[b - 1];
cand_rd_data_2_ff[b] <= cand_rd_data_2_ff[b - 1];
cand_rd_data_3_ff[b] <= cand_rd_data_3_ff[b - 1];
cand_rd_data_4_ff[b] <= cand_rd_data_4_ff[b - 1];
end
end
endgenerate
来看一下最后结果,没有一块一块的斑点了。
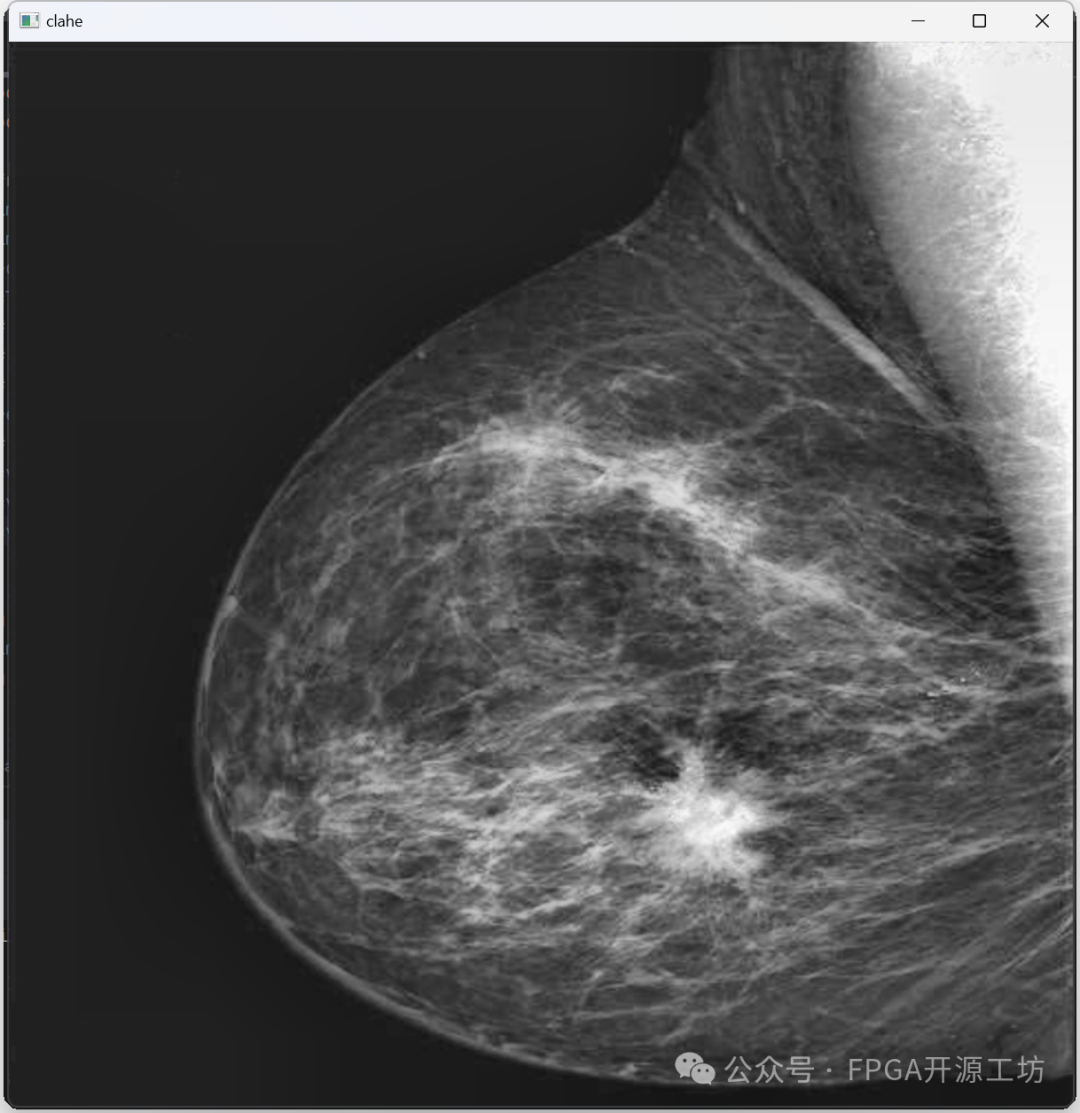
CLAHE算法就是这些,一共分为下面几步:
对整幅图像进行分块,然后在每一块上面分别进行直方图均衡化操作
在进行直方图均衡化的时候进行CLIP操作
进行线性插值
审核编辑:黄飞
-
FPGA图像处理之CLAHE算法2024-01-04 3916
-
FPGA设计经验之图像处理2024-06-12 3180
-
图像自适应分段线性拉伸算法的FPGA设计2012-04-27 2186
-
一种基于FPGA的实时视频图像处理算法研究与实现2019-06-28 3869
-
怎么设计图像自适应分段线性拉伸算法的FPGA?2019-08-16 2303
-
荐读:FPGA设计经验之图像处理2023-06-08 5915
-
基于DSP和FPGA的通用图像处理平台设计2010-12-25 611
-
基于FPGA的红外图像处理系统及算法设计2016-05-17 824
-
一种改进的Bayer图像彩色恢复差值算法2016-09-14 805
-
FPGA学习-基于FPGA的图像处理2023-02-15 1974
-
基于FPGA的图像处理之直方图均衡2023-06-29 1656
-
基于FPGA的图像旋转和双线性插值算法设计2023-09-04 3127
-
FPGA图像处理算法有哪些2023-09-12 1758
-
FPGA图像处理-CLAHE算法介绍(一)2024-01-02 2780
-
基于FPGA的CLAHE图像增强算法设计2025-10-15 480
全部0条评论

快来发表一下你的评论吧 !

