SVM的使用方法

上一篇本着回归传统的观点，在这个深度学习繁荣发展的时期，带着大家认识了一位新朋友，英文名SVM，中文名为支持向量机，是一种基于传统方案的机器学习方案，同样的，支持根据输入的数据进行训练，以进行分类等任务。

那么怎么理解这个支持向量呢，简单来说，这些支持向量就是我们从输入数据中挑选的一些代表性数据。这些数据可以是一个或多个，当我们通过训练获取这些向量即得到了一个svm模型后，所有采集到的新数据，都要和这些代表数据进行对比以判断归属。当然这里的支持向量根据分类的类别数，可以存在多组，以实现多分类。

为了更好的说明，SVM的工作原理，这里用一个python代码给大家展示一下如何使用SVM进行一个单分类任务。之后还会给大家介绍一个小编和同事开发的实际应用SVM的异常检测项目，让大家实际看下SVM的应用效果。

那就先从python代码开始，先开门瞧瞧SVM的世界，请看代码：

（悄悄地说：请各位事先安装numpy，matplotlib以及scikit-learn库）

 

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import load_iris


# Load the Iris dataset
iris = load_iris()
X = iris.data[:, :2]  # Select only the first two features for visualization


# Select a single class for one-class classification (Class 0)
X_train = X[iris.target == 0]


# Create and train the One-Class SVM model
model = svm.OneClassSVM(kernel='rbf', nu=0.05, gamma = 1)
model.fit(X_train)


# Generate test data
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)


# Plot the training data and decision boundary
plt.scatter(X_train[:, 0], X_train[:, 1], color='blue', label='Inliers')
plt.contourf(xx, yy, Z, levels=[-1, 0], colors='lightgray', alpha=0.5)
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')


support_vector_indices = model.support_
support_vectors = X_train[support_vector_indices]


# pait the support vector
plt.scatter(support_vectors[:, 0], support_vectors[:, 1], color='red', label='Support Vectors')


plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('One-Class SVM - Iris Dataset')
plt.legend()
plt.show()

以上代码，我们就使用svm. OneClassSVM构建了一个单分类SVM模型，并使用著名的鸢尾花数据集进行模型训练；最终利用matplotlib库进行结果绘制，结果通过model.predict获取，并将最终训练得到的支持向量用红色点绘制出来，先来看看运行效果：

 

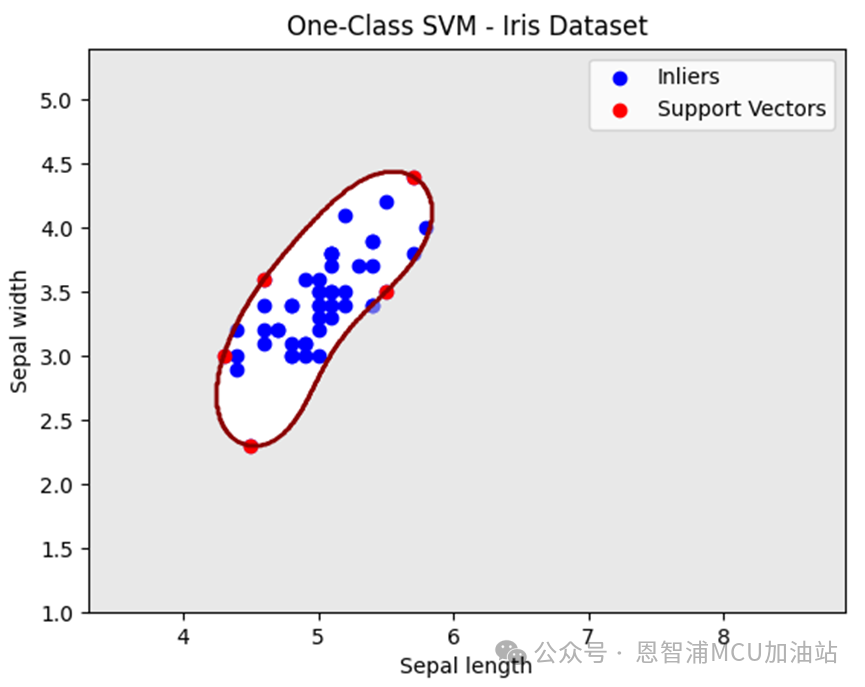
中间的暗红色区域就是模型所训练出来的决策区域，可以简单认为落在红色区域里面的点就是属于我们这一类的。这里我们在训练SVM模型时候，选择了两个特征，分别是花萼的长度以及宽度，当然也可以多选择几组特征（只不过不好图形化显示了）。

相信大家也注意到了，svm.OneClassSVM函数中有两个参数，nu和gamma，这两个可是模型好坏的关键：

nu 控制训练误差和支持向量数之间的权衡。它表示训练误差的上限和支持向量数的下限。较小的nu 值允许更多的支持向量和更灵活的决策边界，而较大的 nu 值限制支持向量数并导致更保守的决策边界。

gamma 定义每个训练样本的影响力。它确定训练样本的影响范围，并影响决策边界的平滑程度。较小的 gamma 值使决策边界更平滑，并导致每个训练样本的影响范围更大。相反，较大的值使决策边界更复杂，并导致每个训练样本的影响范围更小。

接下来我们就实际测试下，调整gamma值从1到100：

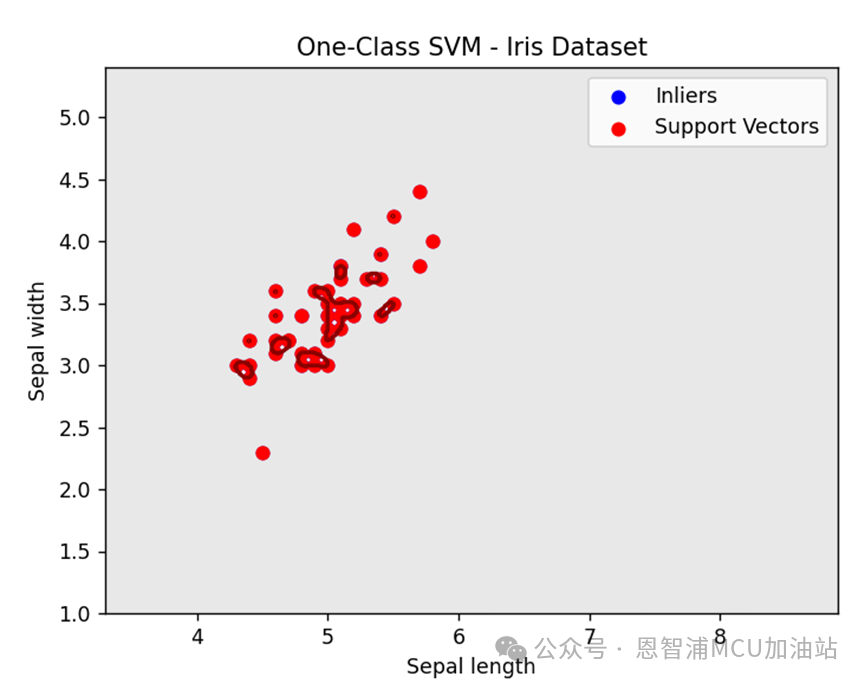
正如上面所述，gamma值变大使得决策区域变得复杂，并且似乎每一个训练数据都变成了支持向量。

接下来我们看看调整nu的情况，nu从0.05->0.5:

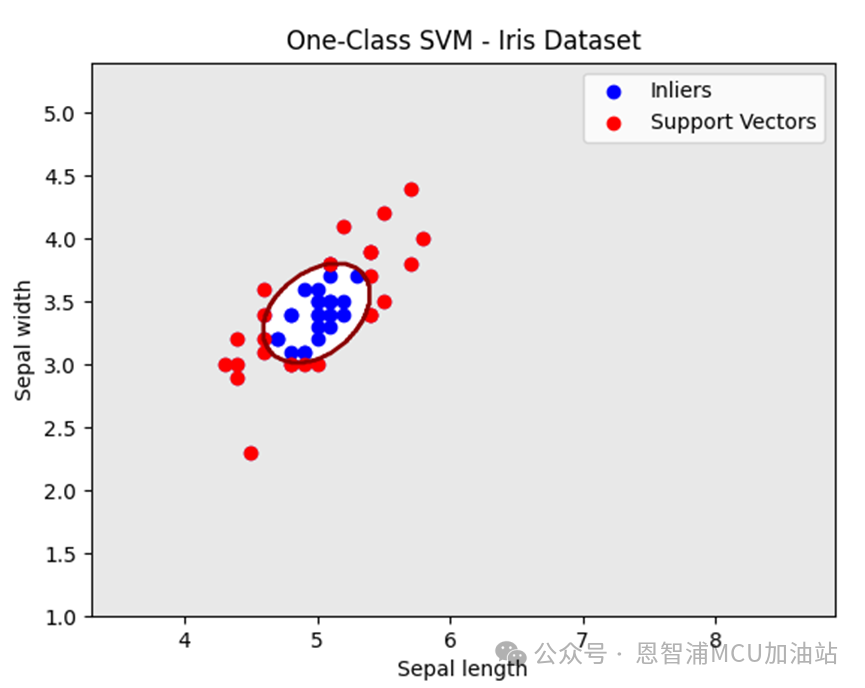
决策边界正如上文所讲，变得更加保守了。不过，在实际使用中，我们需要联合调整nu和gamma参数，以获取最佳的模型拟合效果，当然这就是经验之谈了。所谓：炼丹的过程，没错，即便我们回归传统，炼丹的过程也依旧还是存在的。

好了，那本期小编就给大家先分享到这里，下期将为大家带来一个实打实的，将单分类svm用作异常检测的实际项目，敬请期待！！

　　审核编辑：汤梓红