

TEC效率与散热器热阻抗之间的关系,你了解多少?
工业控制
描述
半导体致冷器(TEC)很常见,看起来也很简单,但简单且非常准确的设计模型和方程却并不常见。这种设计模型在各种应用中都发挥了很好的作用,其输入仅需要典型TEC数据手册中提供的数字。尽管对TEC的物理特性进行了简化,但它足够真实且准确,因此非常有用。它根据TEC数据手册参数、驱动电流(I)、热负载功耗、热导率、散热器热阻抗和环境温度(T3)来预测TEC热负载温度(T)。
该模型被总结为T=TEC输出温度的单个二阶方程。
T = (-P I + I2 Rp/2 + Q1)/(C1 + Cp) + Zh(Q1 + I2 Rp) + T3
其中:
P(瓦/安培)=珀耳帖常数=(Qmax+Imax2Rp/2)/Imax
Qmax(瓦)=零ΔT上的最大传热(来自TEC数据手册)
Imax=完美(Zh=0)散热器的最大冷却电流(来自TEC数据手册)
Vmax=Imax时的TEC压降(来自TEC数据手册)
Rp=TEC电阻=Vmax/Imax
Q1=热负荷产生的热量
C1(W/°C)=热负载到环境的热导率
Cp=TEC热导率=Qmax/ΔTmax
ΔTmax=在Imax和完美散热器的条件下的最大冷却(来自TEC数据手册)
Zh(℃/W)=散热器对环境的热阻
T3=环境温度
关于如何将这种计算方法应用于实际 TEC 的典型例子,以Laird Thermal Systems(莱尔德热系统)的430007-509为例:
Qmax: 3 W
Imax: 1.5 A
Vmax: 3.4 V
ΔTmax: 67°C
然后:
Rp = 3.4/1.5 = 2.27
P = 3 + 1.5 * 3.4 / 2 = 5.55 / 1.5 = 3.7 W/A
Cp = 3 W/67°C = 0.0448 W/°C
通过该设计模型数学量化的一个有用的关系是散热器热阻抗对产生最大冷却效果的最佳TEC驱动电流的影响。当T方程相对于I进行微分,然后求解dT/dI=0处的最大值时,就能得出这一结果:
Io = (P Zh-1)/{Rp[Zh-1 + 2(C1 + Cp)]}
图1中绘制了莱尔德TEC的Io(Zh-1)(黑色)和相应的最大ΔT(蓝色)。请注意,随着Zh-1的减小,两条曲线都趋向于零。产生这种效应的主要原因是,TEC耗散的I2Rp热量必须通过散热器排放到环境中,这会提高散热器温度,进而使TEC的温度升高,这与Zh成正比。
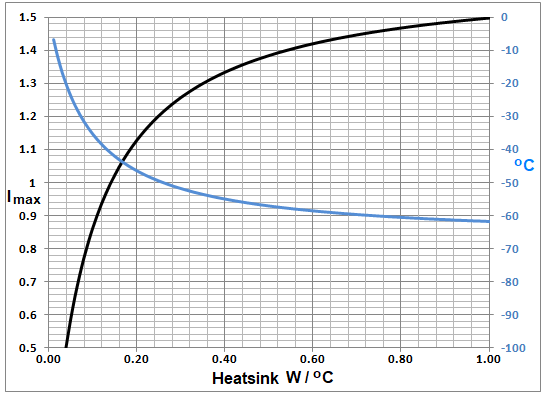
图1 TEC最大冷却驱动电流(黑色)和由此产生的冷却(蓝色)与散热器热导纳(Zh-1)的函数关系。
即使在TEC冷却能力足够且ΔT恒定的情况下,对TEC电流消耗和功耗的影响也是巨大的,如图2所示,ΔT为40℃的示例(Q1和C1=0)。
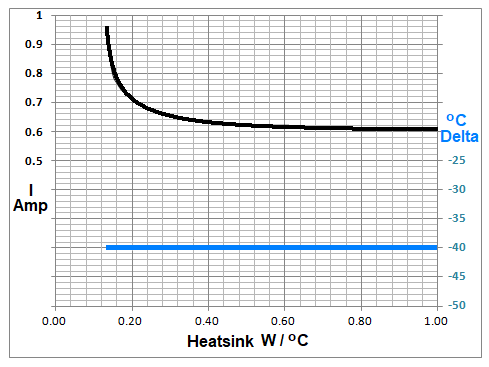
图2 恒定40°C ΔT下的TEC电流消耗I(黑色)与散热器热导纳(Zh-1)的关系。
请注意,当Zh-1从1.0W/°C下降到0.13W/°C时,电流消耗增加了63%,功率增加了165%。
-
热管散热器是如何散热的#热管散热器 #科普学习电子知识 2023-07-03
-
技术资讯 I 推导散热器的辐射热阻2023-03-31 3821
-
A780散热器PCB应用的设计优势2023-02-16 1692
-
仿真看世界之IPOSIM的散热器热阻Rthha解析2021-08-17 2321
-
CPU散热器的作用_CPU散热器的选择2020-04-27 3782
-
如何利用器件应用中的热数据,对散热器进行选择?2019-01-25 4161
-
一文了解什么是散热器2018-11-23 6050
-
芯片热阻计算及散热器、片的选择2017-01-12 1703
-
梳形截面散热器的长度优化设计2013-01-25 887
-
IGBT模块散热器选择及使用原则2012-06-20 14316
-
IGBT模块散热器最基本的使用说明2012-06-19 4411
全部0条评论

快来发表一下你的评论吧 !

