异或门的运算规则及应用

异或门的运算规则

异或门的运算规则如下：

1. 如果输入的两个信号不相同，则输出为 1。

2. 如果输入的两个信号相同，则输出为 0。

具体来说，异或门在输入的信号中只有一个为高电平（1）时，输出才为高电平；当输入的信号全为低电平（0）或全为高电平（1）时，输出为低电平（0）。

以下是异或门的真值表，用于说明它的运算规则：

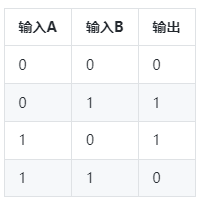
可以看到，在输入的两个信号不同时，输出为1；当输入的两个信号相同时，输出为0。

异或门的运算规则使其在实际应用中非常有用。它可以用于数值计算、电信号处理、编码解码等多种领域，特别在数字电路中，异或门被广泛用于构建更复杂的逻辑电路和功能。

异或门又称可控反相门，为什么？

异或门又称可控反相门是因为异或门输入端信号可以同时取反相变化。

因为异或门输入端信号可以同时取反相变化，而不改变逻辑门的状态，两输入端电平相同时，输出低电平0，两输入端电平不同时，输出为1，这样就可以保证以上两种情况下，输入端信号可以同时取反相变化，而不改变逻辑门的状态。

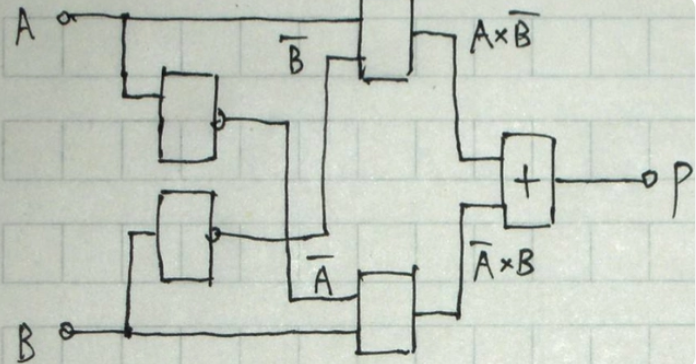
异或门具有广泛的应用场景，包括但不限于以下几个方面：

实现加减法：异或门可以用于实现二进制数的加减法。例如，我们可以使用异或门来实现两个二进制数的加法，如果两个相应的输入端上输入的数相同时则进行减法运算。

数据加密和解密：异或门可以用于数据加密和解密。由于异或运算有一个重要的特性，即相同输入产生相同输出，因此，它可以用于加密和解密数据。

错误检测和纠正：异或门可以用于检测和纠正数据传输中的错误。例如，通过异或运算，可以检测到一个字节是否在传输过程中被错误地修改。

数据交换：异或门可以用于交换两个变量的值，而不需要引入额外的内存空间。通过使用异或运算，可以在一个变量上实现另一个变量的值的交换。

逻辑运算：在数字电路中，异或门可以实现各种逻辑运算，如加法器、减法器、比较器等。

通信系统：异或门在通信系统中也有重要应用，例如在通信协议的帧校验序列中，以及在某些形式的调制解调中。

密码学：在密码学中，异或门常被用于实现加密和解密算法，如凯撒密码和维吉尼亚密码等。

硬件设计：在硬件设计中，异或门常被用于触发器、寄存器等硬件组件的实现。

总的来说，异或门是数字电路和通信系统中不可或缺的一部分，具有重要的意义和应用价值。

审核编辑：黄飞