与门的逻辑表达式如何

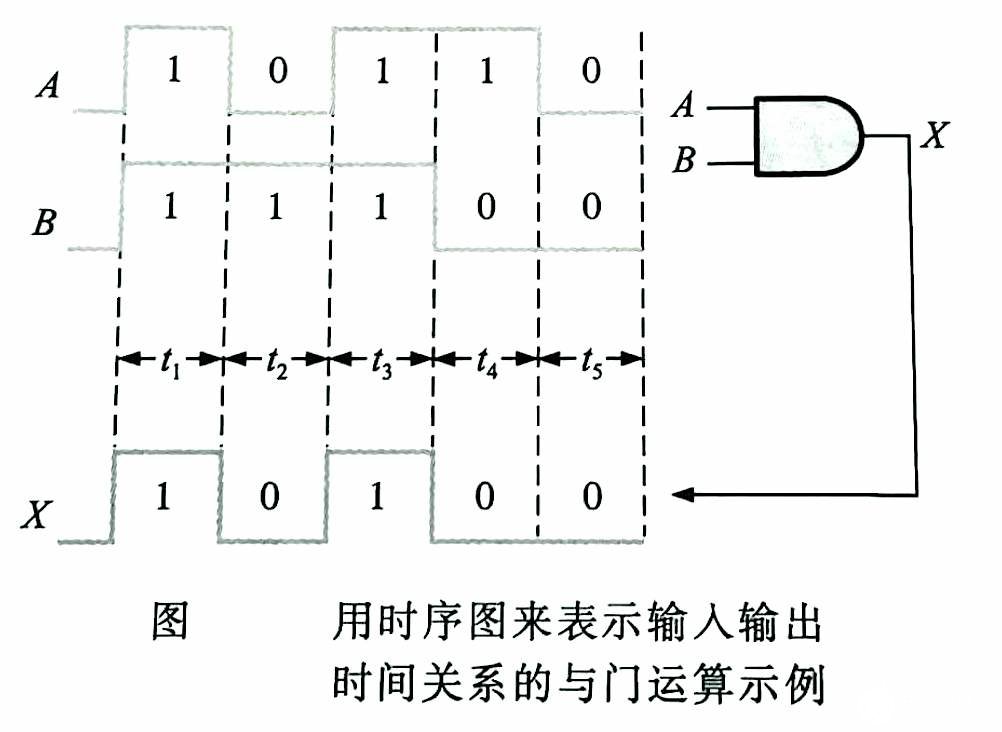
在大多数应用中，输入波形往往不是固定的电平，而是在逻辑高电平和低电平之间频繁变化的电压波形。现在看看具有脉冲波形输入的与门的运算，需牢记的是不管输入是恒定的电平还是不断变化的电平，与门输出总是遵循真值表列出的规则。

通过观察输入之间的相互关系确定在任意给定时间的输出，来说明与门的波形运算。在图中，在时间间隔t1上，输入A与B都是高电平(1)，因此，在这个时间段上，输出X也为高电平(1)。 在时间间隔t2上，输入A是低电平(0)，输入B是高电平(1)，故输出是低电平(0)。 在时间间隔t3上，两个输入又同时为高电平(1)， 因此，输出为高电平(1)。在时间间隔t4上，输入A是高电平(1)， 输入B是低电平(0)， 故输出是低电平(0)。 最后，在时间间隔t5上，输入A是低电平(0), 输入B是低电平(0)， 故输出为低电平(0)。正如所知，表示输入输出波形的关系时间图形叫做时序图。

那与门的逻辑表达式是如何的呢？

对于二输入与门的运算可以用下面的形式来描述:如果一个输入变量为A,另一个输入变量为B，输出变量为x，那么布尔表达式为

X= AB

图a给出了具有两个输入变量和一个输出变量的与门的逻辑符号，同时给出了输出的表达式。

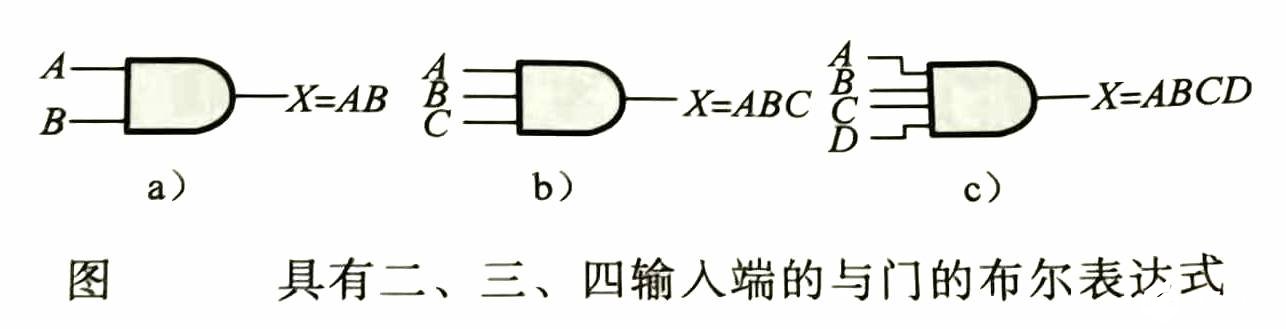
若要将与门的表达式扩展成多输入变量的表达式，只需对每个输入变量简单地用新的字母来表示即可。例如，三输入的与门函数，可以表示为X=ABC，其中A、B、C是输入变量。四输入的与门函数表达式为x= ABCD，依此类推。图3-b与图c分别表示了具有三输入与四输入变量的与门。

可以利用输出的逻辑表达式求与门运算的结果。例如，每个输入变量要么是0，要么是1，代入表达式x=AB,得到对应的输出，参考上节与门的真值表。从求值过程可以看出，只有当输入全为1时，与门的输出才能为1。对于多个不同的输入变量，也可以类似地分析。

审核编辑:黄飞