如何用自积分式罗氏线圈测量纳秒级高压脉冲电流

本文对自积分式罗氏线圈设计做了比较详细的描述。

1灵敏度

线圈的灵敏度也就是线圈输出信号与被测信号的比例。测量大电流,要求将电流缩小到可测量的范围。自积分式罗氏线圈的测量等效线路如图1所示。图中Um为所测的电压信号,:为感生电动势，RL为线圈电阻,R为积分电阻,i(R +RL) n Ld i/d t,则有所测电压为

由此求出线圈的灵敏度S 为

电感L和互感M可以通过测量确定,也可以通过公式计算,即

式中:μ0 为空气磁导率;A为小线圈截面积;N为线圈匝数;r为大线圈半径(到小线圈中心)。所以有

如果考虑电缆的波阻抗,那么R 值应该是积分电阻和电缆波阻抗的并联值,通常我们测量电缆的波阻抗为50,75Ω,这个值远大于积分电阻(一般都小于1Ω),所以可以忽略电缆波阻抗的影响。

2 对方波电流的幅值响应

在脉冲功率技术中,我们所要测量的电流信号经常有方波类型的信号。罗氏线圈感应的电动势是由dIm/d t引起的,方波的平顶电流是无法感应出电信号的,此时线圈内由方波上升沿感应的电动势会以时间常数L/R 通过线圈电感和积分电阻放电,放电太快,则测量无法反映方波电流波形。所以在设计中我们必须保证在T0(所测方波电流的脉宽)时间内电流衰减很小。一般取L/R >20τ0,这样可以满足测量需要。

3 线圈的信号响应

快脉冲信号测量中最重要的是频率响应。要准确考虑罗氏线圈的响应需将它作为传输线来分析

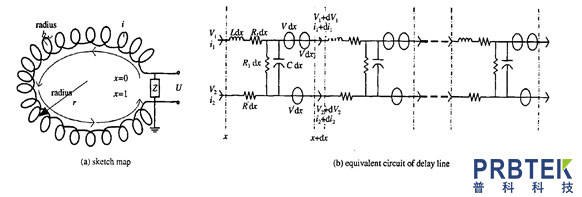
图2传输线模型

传输线电路等效模型如图2(b) 所示。V1,i1,V2，i2分别为线圈上的电压电流和屏蔽盒上的电压电流,L为线圈电感,RL 为线圈电阻,RI 为绝缘(线圈到屏蔽盒)电阻,R'为屏蔽盒电阻,C为传输线电容,即线圈和屏蔽盒间的电容,V为绕包线圈单位长度感应的电动势,V'为大线圈和屏蔽盒单位长度感应的电动势,x的方向如图2 (a) 所示。假设线圈均匀绕包,单位长度电容、电感、电阻相等,积分电阻为R。我们可以用以下方程描述此电路。

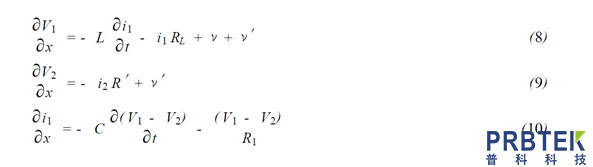
边界条件:x=0,Vout =V1 -V2 = i1 (0) R,V2 (0) = 0 ;X=1，1=2，Vout (1)=0

这个方程组中有些因素的影响很小,忽略它们也可保证方程正确反映电路。假设线圈电阻和屏蔽盒电阻为0、绝缘电阻无穷大、大线圈和屏蔽盒的感生电动势为0。设所测电流Im =Kt,t为时间,K为常数,反映电流的变化率。用拉氏变换解上面的方程组,并通过拉氏逆变换,级数展开和合并,得到Vout的时域函数为

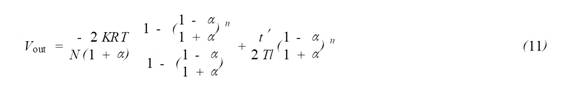
式中: T = ( LC) 1/ 2,Zr为线圈的波阻抗(L/C) 1/ 2,a= R/Zr,设t= 2nTl+t’,0≤t’<2TI,n为正整数(包括0),这样划分可以比较清楚的分析每个波反射过程与输出信号的关系。1如图2(a)所示为大线圈平均周长。

我们知道Vout(t)正比于K,即被测电流Im的变化率。测量要求Vout(t)达到稳定值Vs 的时间T应该可以反映被测电流的上升沿,这就是线圈的高频响应。T值越小,线圈的频率响应(f=0.35/τ)就越高。我们定义T为Vout从0 升到90 %Vs 的时间。讨论输出响应,假设积分电阻纯阻性,要分别考虑a=1,0 ≤a<1和1，,此时输出的稳定值Vs =-LK/ N,设τ= 2 nTl+t’,其中n，t'满足下式

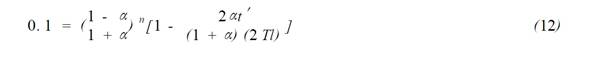
通过数值计算可以求出n 和t'。计算T需要知道线圈的电感L、电容C和积分电阻R,而L，C，R 可以通过测量取得,也可估算。

审核编辑 黄宇