深度学习中的不同Normalization方法小结

1为什么要 Normalization

在深度神经网络中，存在一种内部协变偏移（internal covariate shift）现象，它是由于训练过程中不断变化的网络参数导致网络各层的输入分布发生变化。

例如，输入层中某些具有较高数值的特征可能会起到主导作用，从而在网络中产生偏差，即只有这些特征对训练结果有贡献。

例如，假设特征 1 的值介于 1 和 5 之间，特征 2 的值介于 100 和 10000 之间。在训练期间，由于两个特征的规模不同，特征 2 将主导网络，只有该特征对模型作出贡献。

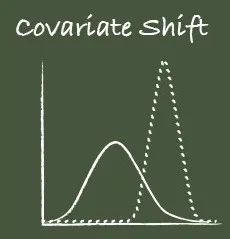
这仅仅是一层的情况，如果从整个深度神经网络来看，那就更加复杂了。Google 在其论文中将这一现象总结为，

Internal Covariate Shift 简称 ICS，是由于训练过程中网络参数的变化引起的网络激活分布的变化。

网络中的每一层的参数更新会导致本层的激活输出的分布发生变化，也就是后面层的输入的分布发生变化。而深度神经网络往往涉及到很多层的叠加，通过层层叠加，会引发后面层非常剧烈的变化，这就给深度模型的训练带来了巨大挑战。

由于上述原因，引入了称为 normalization 的概念来解决这些问题。

Normalization 有很多优点，包括

减少内部协变偏移以改善训练；

将每个特征缩放到相似的范围以防止或减少网络中的偏差；

通过防止权重在整个地方爆炸并将它们限制在特定范围内来加速优化过程；

通过辅助正则化减少网络中的过拟合。

Normalization 也可以结合概率论来解释。一般来说，机器学习中的方法比较偏爱独立同分布的数据。当然并不是所有算法都有这个要求，但独立同分布的数据往往可以简化一般模型的训练，提升模型的预测能力。

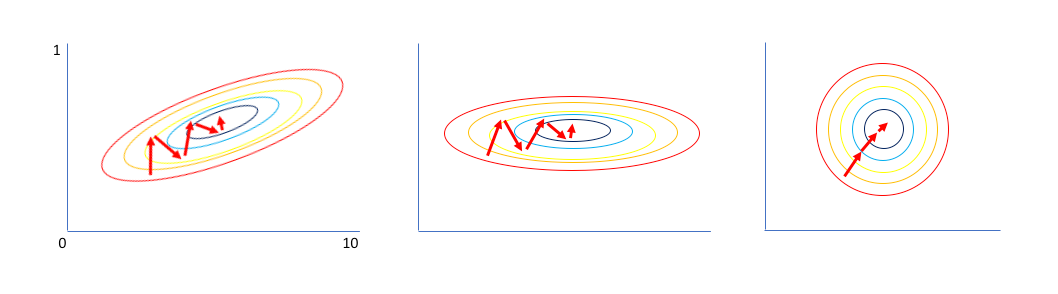
在把数据输入模型之前，对其经过白化（whitening）处理是一个不错的预处理步骤。

比如上图（左）的数据，先经过零均值化以及去相关性操作，得到中间的形式，各个特征相互独立；再让所有特征具有单位标准差，最终得到独立同分布的数据。

但深度学习中往往不直接使用白化操作，白化中间需要用到 PCA。如果对输入数据作一次 PCA，那也仅仅是针对线性模型，但如果针对神经网络中的中间每一层在激活后再使用白化，那计算代价太过高昂。

那怎么办呢？不妨模仿白化，但可以作一些简化，比如不考虑去相关性，而是对各层的激活输出在一定范围内作标准化处理，再加一定的缩放和偏移。这里的操作范围可以不同，于是就有了一堆 Normalization 方法。

2Batch Normalization

Batch Normalization 侧重于标准化任何特定层的输入（即来自前一层的激活）。

下图左边网络中没有 BN 层，右边网络中在隐藏层前加入了 BN 层，即对输入层在小批次上作了 Normalization。

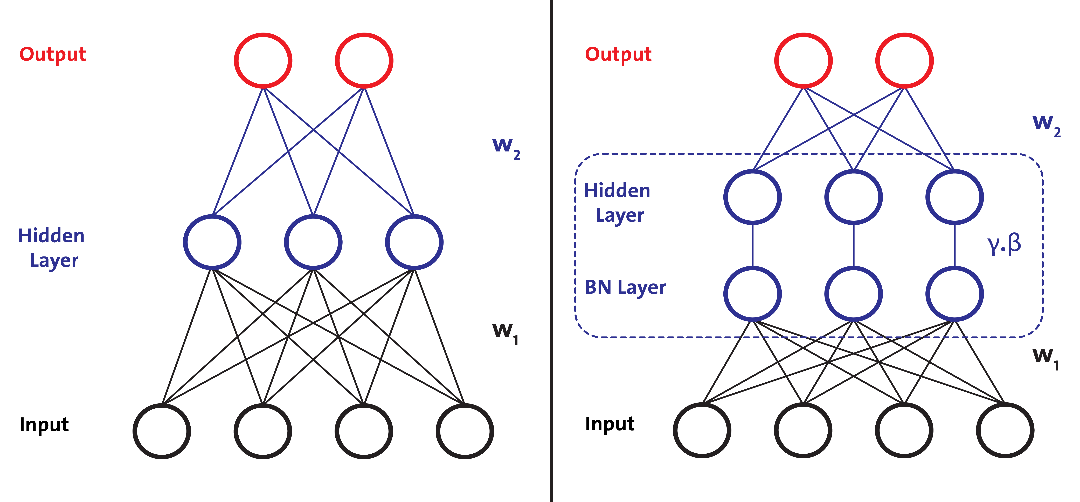
标准化输入意味着网络中任何层的输入都应该近似零均值以及 单位方差 。简单来说，BN 层通过减去当前小批量中的输入均值并除以标准差来变换当前小批量中的每个输入。


 

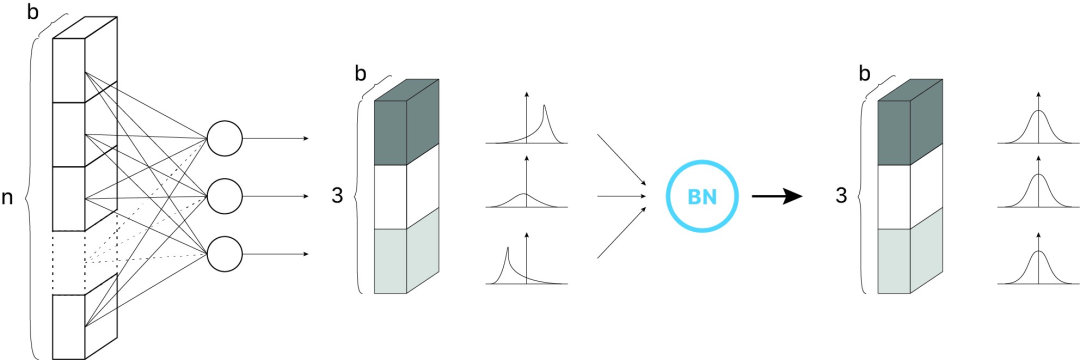
总结一下：简而言之，BN 使得梯度更具预测性，从而有效改善网络训练。

下面，让我们看看 BN 的一些优点：

BN 加速深度神经网络的训练。

对于每个输入小批量，我们计算不同的统计量，这引入了某种正则化。正则化技术起到在训练期间限制深度神经网络复杂度的作用。

每个小批量都有不同的小分布，这些小分布之间的变化称为内部协变偏移，BN 被认为消除了这种现象。

BN 对通过网络的梯度流也提供了有利影响：它减少了梯度对参数尺度或其初始值的依赖性，从而使我们能够使用更高的学习率。

然而，下面是批量标准化的几个缺点：

BN 在每次训练迭代中计算批次数据的统计量（Mini-batch 均值和方差），因此在训练时需要更大的批次大小，以便它可以有效地逼近来自 mini-batch 的总体均值和方差。这使得 BN 更难训练用于对象检测、语义分割等应用的网络，因为它们通常涉及高分辨率（通常高达 1024，2048 等）的输入数据，使用大批量进行训练在计算上往往是不可行的。

BN 不适用于 RNN。问题是 RNN 与之前的时间戳具有循环连接，并且在 BN 层中的每个时间步长都需要单独的 和 ，这反而增加了额外的复杂性并使 BN 与 RNN 一起使用变得更加困难。

不同的训练和测试计算：在测试（或推理）期间，BN 层不会从测试数据 mini-batch（上面算法表中的步骤 1 和 2）计算均值和方差，而是使用固定均值和从训练数据计算的方差。这在使用 BN 时需要谨慎，并引入了额外的复杂性。在 pytorch 中，model.eval() 确保在评估模型中设置模型，因此 BN 层利用它来使用从训练数据预先计算的固定均值和方差。

3Weight Normalization

针对 BN 的缺点，Saliman 等人提出了 WN。他们的想法是将权重向量的大小与方向解耦，从而重新参数化网络以加快训练速度。

重新参数化是什么意思呢？


 

WN 加速了类似于 BN 的训练，与 BN 不同的是，它也适用于 RNN。但是与 BN 相比，使用 WN 训练深度网络的稳定性较差，因此在实践中并未得到广泛应用。

4Layer Normalization

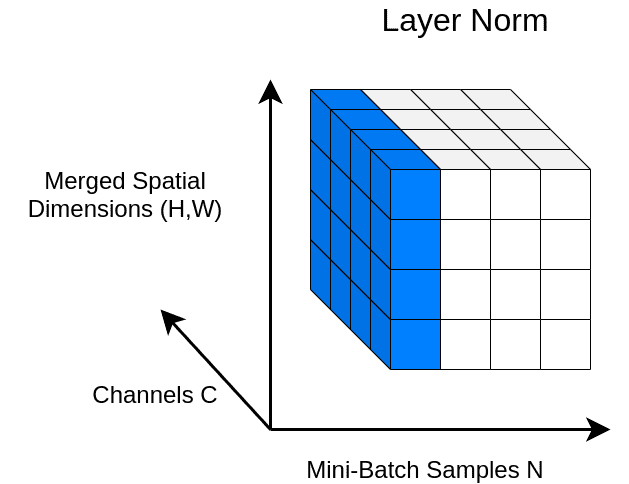
受 BN 的启发，Hinton 等人提出的 Layer Normalization 沿特征方向而不是小批量方向对激活进行 normalization。这通过消除对批次的依赖来克服 BN 的缺点，也使得 RNN 更容易应用 BN。

与 BN 不同，LN 直接从整个隐藏层的神经元的总输入估计统计量，因此 normalization 不会在训练数据之间引入任何新的依赖关系。它适用于 RNN，并提高了几个现有 RNN 模型的训练时间和泛化性能。最近，它还与 Transformer 模型一起配合使用。

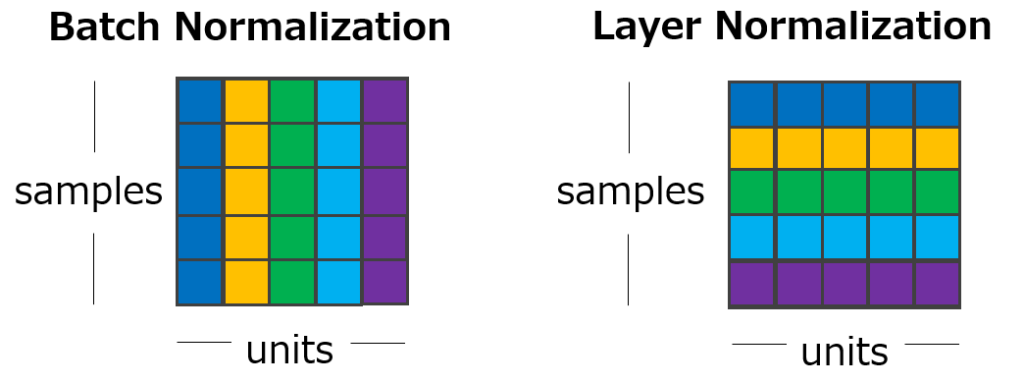
注意上图中的颜色走向，与 BN 有所不同，LN 对某一个层中所有特征进行归一化，而不是在小批量中对输入特征进行归一化。



 

5Group Normalization

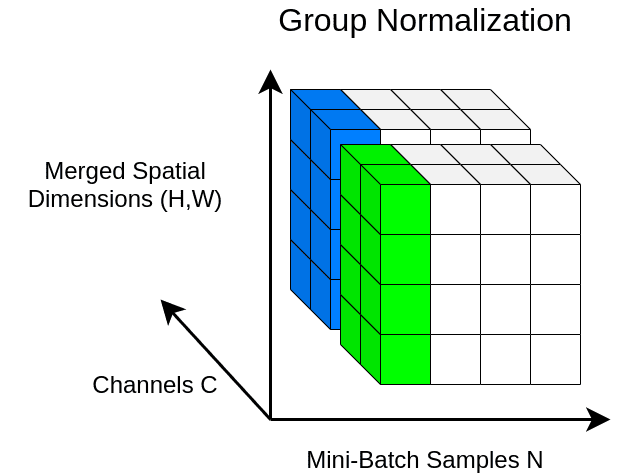
与 LN 类似，GN 也沿特征方向进行操作，但与 LN 不同的是，它将特征划分为若干组并分别对每个组进行 normalization。在实践中，GN 比 LN 常常表现得更好，它的参数 num_groups 可以设为超参数。

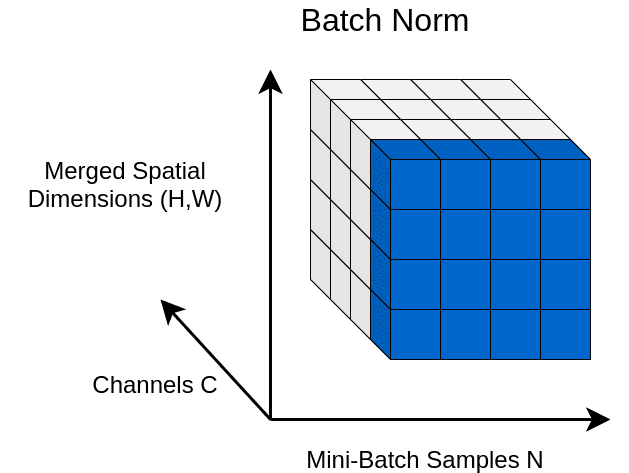
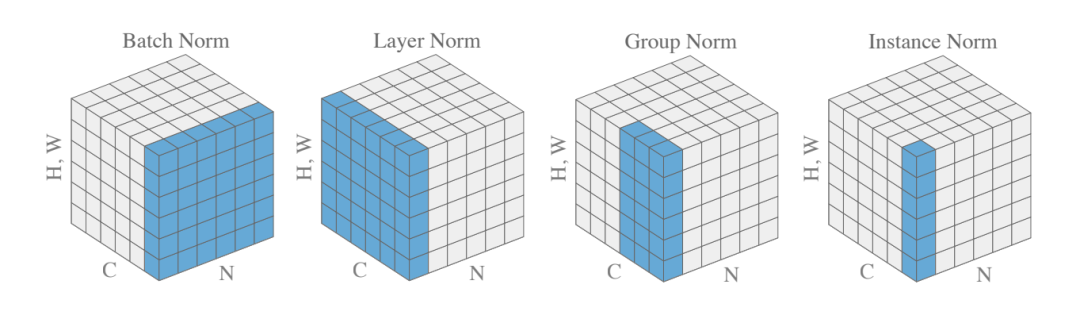
如果觉得 BN、LN、GN 有点令人困惑，下图给出了一个总结。给定形状 (N, C, H, W) 的激活，BN 归一化 N 方向，LN 和 GN 归一化 C 方向，但 GN 额外地将 C 通道分组并单独 normalize 各个组。

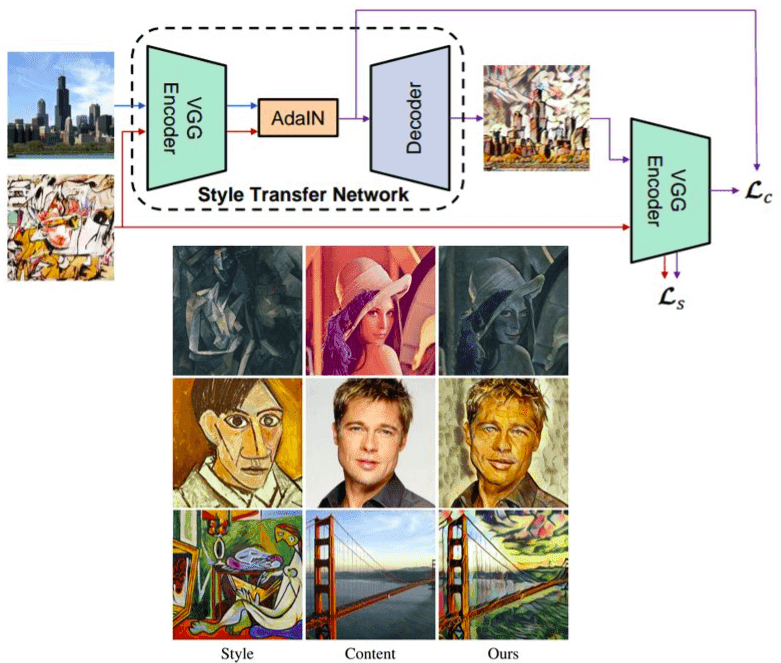
下图中可以看到一个简单的编码器-解码器网络架构，带有额外的 AdaIN 层用于样式对齐。

其中，

分别计算每个输出通道的均值和标准差，可以结合下图来理解。

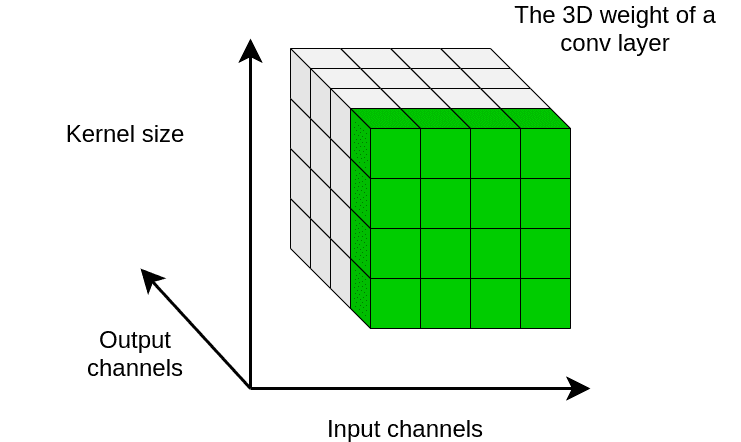
本质上，WS 旨在单独调控每个输出通道的权重的一阶统计量。通过这种方式，WS 在反向传播期间对梯度进行 normalization。

从理论上和实验上都验证了它通过标准化卷积层中的权重来平滑损失情况。

理论上，WS 减少了损失和梯度的 Lipschitz 常数。核心思想是将卷积权重保持在一个紧凑的空间中，从而平滑了损失并改进了训练。

论文作者将 WS 与 GN 结合使用，取得了不错效果。

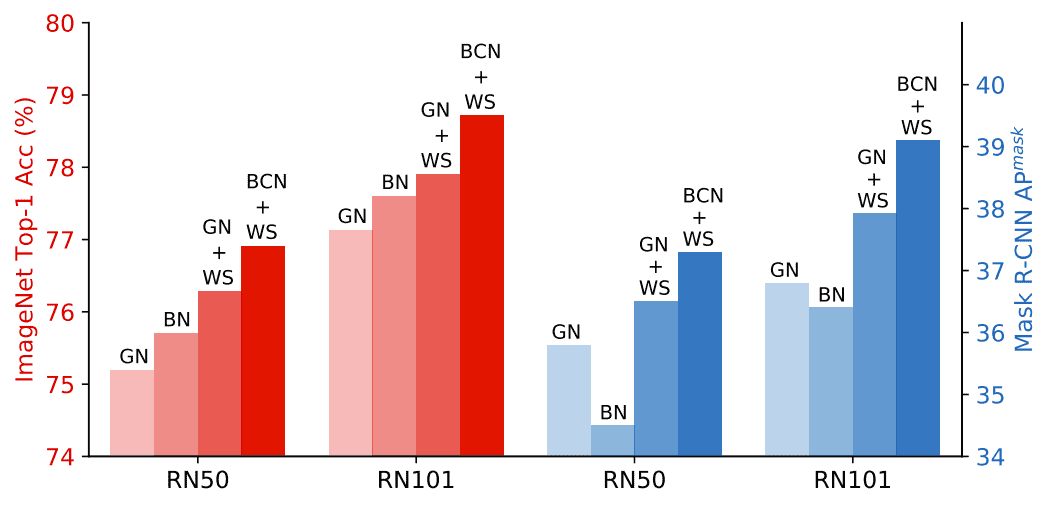
在 ImageNet 和 COCO 上比较 normalization 方法，GN+WS 大大优于单独使用 BN 和 GN。

8小结

最后，为了便于比较和分析它们的工作原理，我们将上述几种主要 normalization 方法汇聚在一个图中。

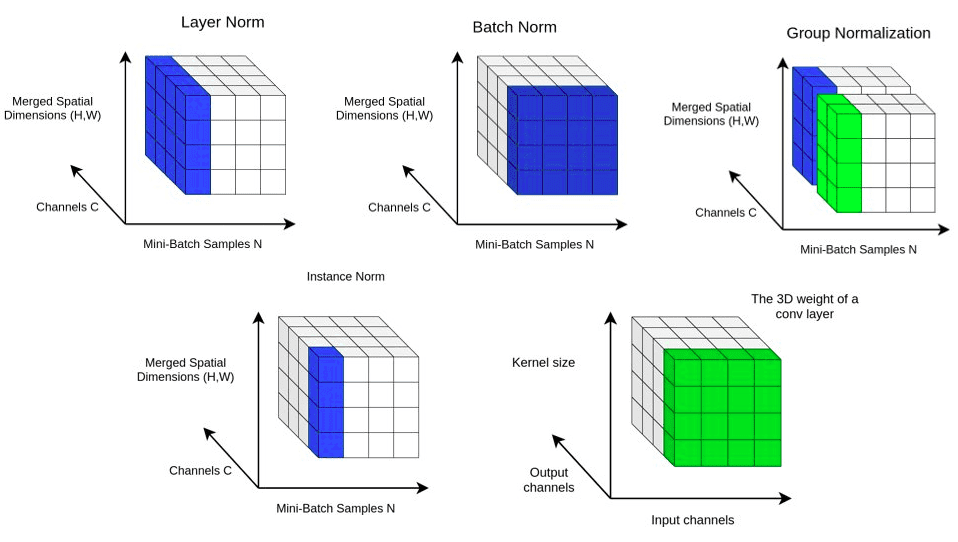
当在论文或具体网络架构中遇到这些名词时，脑子中可以浮现出对应的图来辅助理解。




审核编辑：刘清